クーロン力は極めて重要な概念の一つで、物理化学を理解する上で避けて通ることはできません。

クーロン力とは電荷を持つ物体間に働く力として定義され、物理現象を説明するための基礎となっています。

クーロン力は電磁気学の一部として位置づけられますが、その影響は他の分野にも広がります。

たとえば、静電気現象や分子間相互作用、さらには天体物理学に至るまで、非常に幅広い分野で重要な役割を果たしています。

物理化学で取り上げられる 分子の結合や物質の性質、さらには化学反応のメカニズムを理解にあたってクーロン力の基本を正確に把握しておくことは必要不可欠です。

クーロンの法則

クーロンの法則は、電荷を持つ物体間に働くクーロン力を説明する法則です。

電荷には正の電荷を持つ正電荷と、負の電荷をもつ負電荷が存在し、同符号の電荷は反発、異符号の電荷は引き合う性質を持ちます。

このときに働く力をどのように定量化していくのか以下で説明をしていきます。

クーロンの法則の定義

クーロンの法則は電荷同士にはたらく力を定量的に表す基本的な法則です。

ここである点に固定された電荷 \(Q ~ [\text{C}]\) と自由に運動できる電荷 \(q ~ [\text{C}]\) が真空中で \(r ~ [\text{m}]\) の距離を隔てて存在する場合を考えます。

自由に運動できる電荷 \(q\) に働く力 \(F ~ [\text{N}]\) の大きさはクーロンの法則によると次式で与えらます。

\[ F = k \frac{Qq}{r^2} \]

ここで \(k\) は真空中における比例定数で、真空中では \(k \approx 8.9875 \times 10^9 ~ [\mathrm{N･m^2 / C^2}]\) とされています。

クーロンの法則の性質

クーロンの法則の重要性は主に次の3つです。

• クーロン力の大きさと電荷量の関係
• クーロン力の大きさと電荷間の距離の関係
• 符号による力の向き

クーロン力の大きさと電荷量の関係

クーロン力は、互いに作用する電荷の大きさに依存します。

式(1)で示される通り、電荷量が大きくなるほど、クーロン力も大きくなります。

たとえば、片方の電荷量が2倍になれば、クーロン力も2倍になります。また、両方の電荷量が2倍になると、クーロン力は4倍になります。

\[ \begin{align*} k \frac{Q \cdot 2q}{r^2} &= 2 k \frac{Q q}{r^2} \\[15pt] k \frac{2Q \cdot 2q}{r^2} &= 4 k \frac{Q q}{r^2} \end{align*} \]

クーロン力の大きさと電荷間の距離の関係

クーロン力は、電荷間の距離 \(r\) の2乗に反比例します。

電荷間の距離が半分になると、クーロン力は 4 倍に増加し、逆に電荷間の距離が 2 倍になると、クーロン力は 1/4 に減少します。

\[ \begin{align*} k \frac{Qq}{\displaystyle{\left(\frac{r}{2}\right)^2}} &= 4 k \frac{Q q}{r^2} \\[20pt] k \frac{Qq}{(2r)^2} &= \frac{k}{4} \frac{Q q}{r^2} \end{align*} \]

直感的には電荷が近づけば互いの電気的影響をより強く感じるため力が急激に大きくなり、電荷が遠ざかると互いの影響が弱まり力が急激に減少すると理解できるでしょう。

この特性は逆二乗の法則と呼ばれ、重力や光の強度減衰などにも見られる基本的な物理法則です。

符号による力の向き

クーロンの法則のもう一つの重要な特徴は、電荷の符号によって力のはたらき方が異なることです。

それぞれの電荷が同符号の場合、すなわち \(Q > 0, ~ q > 0\) または \(Q < 0, ~ q < 0\) のとき、互いの電荷は離れようとする斥力がはたらきます。

一方でそれぞれの電荷が異符号の場合、すなわち \(Q > 0, ~ q < 0\) または \(Q < 0, ~ q > 0\) のとき、互いの電荷は近づこうとする引力がはたらきます。

クーロン力のベクトル表現

クーロン力は電荷の符号によって斥力もしくは引力として働きますが、このとき着目したいのは及ぼされる力の向きです。

ベクトルを用いてクーロン力を記述することで力の向きを表現することが可能で、式(1)をベクトル表現にしたものが次式になります。

\[ \boldsymbol{F} = k \frac{Qq}{r^3} \boldsymbol{r} \]

\(\boldsymbol{F}\) は電荷 \(q\) が固定電荷 \(Q\) から及ぼされるクーロン力を表し、\(\boldsymbol{r}\) は固定電荷 \(Q\) を起点として電荷 \(q\) の位置を示すベクトルです。また \(\boldsymbol{r}\) の絶対値は \(r\) として表しています。

ベクトル表現にするとクーロン力が電荷間の距離の3乗に反比例するかように見えますが誤った解釈です。

式(2)は、単位ベクトル \(\frac{\boldsymbol{r}}{r}\) にクーロン力の大きさ \(k \frac{Qq}{r^2}\) だけ倍にしたものと理解します。つまり…

\[ \boldsymbol{F} = k \frac{Qq}{r^2} ~ \frac{\boldsymbol{r}}{r} \]

そして式(2)または式(3)から明らかなように、クーロン力 \(\boldsymbol{F}\) と電荷の位置ベクトル \(\boldsymbol{r}\) は平行な関係にあります。

位置ベクトルに掛かる係数が正の値を持つとき、言い換えるとそれぞれの電荷が同符号の場合では \(\boldsymbol{F}\) および \(\boldsymbol{r}\) は同じ方向を指します。要するに電荷 \(q\) は固定電荷 \(Q\) から離れるように力が働きます。

逆に係数が負の値を持つとき、すなわちそれぞれの電荷が異符号の場合では \(\boldsymbol{F}\) および \(\boldsymbol{r}\) は真逆の方向を指します。要するに電荷 \(q\) は固定電荷 \(Q\) に近づく向きに力が働いていることを表現できます。

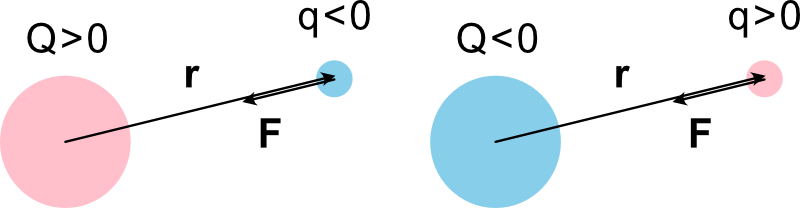
こうしてベクトルによって電荷間にはたらく斥力あるいは引力を記述することが可能になります。

クーロン力と作用反作用の法則

空間のある点に固定された電荷 \(Q\) と自由に運動できる電荷 \(q\) について、電荷 \(q\) は式(1)に示す通り \(F = k\frac{Qq}{r^2}\) のクーロン力を固定電荷 \(Q\) から受けることになります。

このとき、固定電荷 \(Q\) は定点から動かないため一見して何の力も働いていないように思えるかもしれません。

しかし実際は、固定電荷 \(Q\) も電荷 \(q\) からのクーロン力を受けており、互いに作用力・反作用力の関係にあります。

2つの物体それぞれにはたらく作用力および反作用力は、互いに力の大きさは等しいものの逆向きに力が働くという特徴を持ちます。

自由に動ける2つの電荷 \(q_1\), \(q_2\) を考えます。電荷 \(q_1\) が電荷 \(q_2\) に及ぼすクーロン力を \(\boldsymbol{F}_{12}\)、その逆を \(\boldsymbol{F}_{21}\) としたとき作用反作用の法則から次式が成立します。

\[ \boldsymbol{F}_{12} + \boldsymbol{F}_{21} = \boldsymbol{0} \]

\(\boldsymbol{F}_{12}\) および \(\boldsymbol{F}_{21}\) にクーロンの法則を適用すると

\[ \begin{align*} &\text{eq(5.1) : } ~~~~~ \boldsymbol{F}_{12} = k\frac{q_1q_2}{r^3} \boldsymbol{r}_{12} \\[15pt] &\text{eq(5.2) : } ~~~~~ \boldsymbol{F}_{21} = k\frac{q_1q_2}{r^3} \boldsymbol{r}_{21} ~~~ ( ~ r = |\boldsymbol{r}_{12}| = |\boldsymbol{r}_{21}| ~ ) \end{align*} \]

ここで \(\boldsymbol{r}_{12}\) は電荷 \(q_1\) を起点とした電荷 \(q_2\) までの位置ベクトル、\(\boldsymbol{r}_{21}\) は電荷 \(q_2\) を起点とした電荷 \(q_1\) までの位置ベクトルを表しています。

これら位置ベクトルは \(\boldsymbol{r}_{12} + \boldsymbol{r}_{21} = \boldsymbol{0}\) を満たす必要がありますが、式(5)を式(4)に代入して整理すれば成立が確認できます。

重ね合わせの原理

静電気現象では、しばしば複数の電荷の影響を同時に考える必要があります。この際に重要になるのが重ね合わせの原理です。

重ね合わせの原理は電磁気学における基本的な法則の一つで、複数の電荷が存在する場合でもそれぞれの電荷について単独でクーロン力を計算し、その合成によって総合的な力を求めることができます。

3つ以上の電荷が存在する場合を考えます。固定電荷 \(q_2\), \(q_3\) \(\cdots\) \(q_n\) が存在する空間中に、電荷 \(q_1\) を置いたときに電荷 \(q_1\) にはたらくクーロン力はどのように記述されるでしょうか。

結論、重ね合わせの原理によってそれぞれの電荷から受けるクーロン力の和として次式で表されます。

\[ \boldsymbol{F}_1 = \boldsymbol{F}_{21} + \boldsymbol{F}_{31} + \cdots + \boldsymbol{F}_{n1} \]

\(\boldsymbol{F}_{21}\), \(\boldsymbol{F}_{31}\) \(\cdots\) \(\boldsymbol{F}_{n1}\) は固定電荷 \(q_2\), \(q_3\) \(\cdots\) \(q_n\) のそれぞれから電荷 \(q_1\) に及ぼされるクーロン力を表し、それらのベクトル合成によって得られる \(\boldsymbol{F}_1\) が電荷 \(q_1\) が総合的に受けるクーロン力を表します。

次図のように、3つの電荷 \(q_1\), \(q_2\), \(q_3\) からなる系について、電荷 \(q_1\) がその他の電荷から受ける総合的なクーロン力 \(\boldsymbol{F}_1\) を求めたいとき、\(q_1\), \(q_2\) 間におけるクーロン力 \(\boldsymbol{F}_{21}\) と \(q_1\), \(q_3\) 間におけるクーロン力 \(\boldsymbol{F}_{31}\) を独立に計算し、最後にベクトルの合成を行えば良いです。