物質同士を混ぜ合わせたりしたとき、別の物質に変化する化学反応が起きます。
例えば次の反応は、水素 \(\text{H}_2\) と酸素 \(\text{O}_2\) から水 \(\text{H}_2 \text{O}\) が生成する様子を表しています。
式(1)\[ 2 \text{H}_2 + \text{O}_2 \rightarrow 2 \text{H}_2 \text{O} \]
ところでこの化学反応式は一方的に水が生成されることを表現しているのですが、実際はこのような反応ばかりではありません。
次に示す水素 \(\text{H}_2\) とヨウ素 \(\text{I}_2\) の反応のように、生成したヨウ化水素 \(\text{HI}\) が分解することによって反応前の状態に戻ってしまうこともあるのです。
式(2)\[ \text{H}_2 + \text{I}_2 \rightleftharpoons 2 \text{HI} \]
そのような反応では、式(2)に示す通り両方向の変化を指し示す2つの矢印を利用して反応式を表現することになります。
同種の反応について一般名称が与えられており可逆反応と呼びます。一方で、式(1)のような反応が一方通行であるものは不可逆反応と呼びます。
ここで1つ疑問が生じます。不可逆反応では生成物が得られれば反応が終了したと考えることができます。
一方、可逆反応では反応物と生成物の状態を行ったり来たりするという事だから、言い換えれば常に化学反応し続けていることになります。
ただ身の回りで常に状態が変化しているモノを認識することは基本的に無いと思われます。では一体この可逆反応系では分子レベルでどの様な状態になっているのでしょうか。
以下で順を追って考えていくことにします。
化学反応が起こるには
まずは化学反応が起こるとはどういうことか知る必要があります。
複数ある物質を互いに混ぜ合わせることによって新たに別の物質が生成されますが、そもそもこの「物質」とは化学反応式にも示されるような分子 (或いは原子) から構成されています。
そして反応の前後で分子が変化するためには、反応し合う分子同士が接触する必要があると考えるのが自然です。
そこで接触しやすさを数学的に取り扱ってみることにします。
分子の接触のしやすさは濃度で計る
体積 \(V [\text{L}]\) の反応容器を考えます。これは箱やビーカーなど具体的なものを想像してもらって構いません。
これから考えるのは、この容器内にいくつかの分子を配置することです。
その配置方法は、空間全域に渡って均等に配置されていたり、ある一箇所に偏っていたり。また、分子の数が多かったり少なかったりなど様々な場合が考えられます。
その中でも、容器内にたくさんの分子がある状態とない状態とを比較すると、圧倒的に分子同士の接触回数に違いが現れることが推測されます。
分子がたくさんあればあるほど、接触しやすくなるのは感覚的にも理解できるでしょう。
分子がある一箇所に偏っていても接触しやすくなるのではないかと思われるでしょうが、実は分子は絶えず動き回っているため可能な限り空間いっぱいに広がり、結果的に全域に渡って配置したのと同じ状態に近づいていきます。
※分子が動き回る、すなわち運動することを熱運動と言います。これは別のコンテンツで解説することにします。
つまり分子同士の接触のしやすさを表現するために重要となるファクターは、分子の濃度であると見当がつくでしょう。
化学では、ある物質 \(\text{A}\) の濃度を \([\text{A}] ~ [\text{mol/L}]\) と表す慣習があります。
したがって、式(2)について水素およびヨウ素の濃度はそれぞれ、\([\text{H}_2]\), \([\text{I}_2]\) と表されます。
また水素とヨウ素の物質量をそれぞれ \(n_{\text{H}_2}\), \(n_{\text{I}_2} \text{ [mol]}\) とすれば、濃度は次式のように具体的な表現にすることができます。
式(3)\[ [\text{H}_2] = \frac{n_{\text{H}_2}}{V} \\[15pt] [\text{I}_2] = \frac{n_{\text{I}_2}}{V} \]
異なる分子同士の接触
濃度によって分子同士の接触しやすさを定量化しましたが、式(3)のままでは同じ分子同士の接触しか勘定できていません。
私達が考えなければならないのは、水素とヨウ素の接触しやすさです。
一体どのように定式化すれば良いか、以下で説明していきます。
まずは次の図を見ていただきましょう。
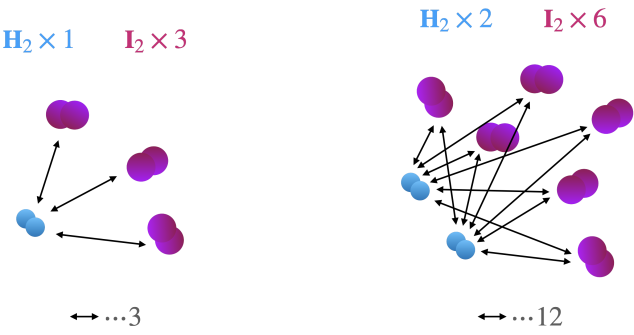
水素とヨウ素の間には矢印を引いています。この矢印はそれぞれ異なる分子間の接触について起こり得る場合を示しています。
そして矢印の本数こそが異分子間接触のしやすさに相当することが分かるでしょう。
図に示すように、もし水素の数を2倍に増やすと水素とヨウ素間に引くことができる矢印の本数は2倍に増えることになります。また更にヨウ素も2倍に増やすと矢印の本数は2倍だけ増えます。
初期状態から比較すると、それぞれの分子を2倍ずつ増やすことによって計4倍だけ矢印の本数が増えることになります。
以上のことから、矢印の本数は水素とヨウ素の分子数 \(N_{\text{H}_2}\) および \(N_{\text{I}_2}\) の積によって与えることが可能だと分かります。
式(4)\[ \begin{align*} N_{\text{H}_2} \times N_{\text{I}_2} &= ( N_A n_{\text{H}_2} ) \times ( N_A n_{\text{I}_2} ) \\[15pt] &= N_A^2 n_{\text{H}_2} n_{\text{I}_2} \end{align*} \]
式の途中に登場する \(N_A\) はアボガドロ数で \(6.022 \times 10^{23} \text{ [/mol]}\) の値をもつ定数です。
前項で説明した内容を踏まえると、接触のしやすさは物質の濃度で与えられるべきなので、式(4)の意味も加味すれば異なる分子間の接触しやすさはそれぞれの物質の濃度の積によって与えればよいと考えることができます。
式(5)\[ [\text{H}_2] [\text{I}_2] \]
以上の内容は逆向きの反応にも適用することができます。
そのようにして求めた右向きと左向きの反応における分子間接触のしやすさを利用して、可逆反応系が最終的に落ち着く状態を明らかにしつつ、それを特徴づける量を定めてみましょう。
正反応と逆反応の釣り合い
内容に入る前に、ここで可逆反応系について「右向きの反応」および「左向きの反応」をもう少しスマートな表現に言い換えておきます。
これらはそれぞれ正反応 (\(\rightarrow\)) および逆反応 (\(\leftarrow\)) と呼ばれるので以降でもそのように表現していくことにします。
本題に戻って、前節の最後に触れたとおりまずは逆反応における反応分子間の接触のしやすさを数学的に表現する必要があります。
水素とヨウ素の接触しやすさを計算したときのように、反応分子間でペアを作る場合の数を求めましょう。
式(2)の逆反応ではヨウ化水素 \(\text{HI}\) 2分子が揃うことで反応が進みます。
つまり反応分子はヨウ化水素のみということなので、反応容器内に存在するヨウ化水素の分子数を \(N_{\text{HI}}\) とすれば、接触しやすさはそれらの中から2つを選択する組み合わせを計算すれば良い事になります。
式(6)\[ {}_{N_{\text{HI}}} \text{C}_2 = \frac{N_{\text{HI}} (N_{\text{HI}} - 1)}{2} \simeq \frac{N_{\text{HI}}^2}{2} \]
ここで、容器内に存在する分子数 \(N_{\text{HI}}\) は桁が非常に大きいため仮に 1 を引いたとしてもほとんど影響がありません。
そのため近似的に \(N_{\text{HI}} - 1 \simeq N_{\text{HI}}\) としています。
するとヨウ化水素間の接触しやすさはヨウ化水素の濃度の2乗に比例するように記述できます。
式(7)\[ \frac{[\text{HI}]^2}{2} \]
準備が整いつつありますが、実はもう一つクリアしなければならない課題があります。
反応速度
ここまでで、反応分子間の接触しやすさを求めてきたものの、化学反応系はその要因だけで反応可否が決まるわけではありません。
物質の種類ごとに反応性に富んでいたり、活性が弱かったりなど様々だからです。
つまり、すぐさま生成物が得られるものや、生成物が得られるまでに長時間を要するものもあるということです。
そこで反応速度 \(v [\text{mol/L} \cdot \text{s}]\) という量を考えることにします。
次元にあるとおり、濃度を時間で割ったもので単位時間あたりに変化する物質の濃度を表しています。
この反応速度は、反応分子間の接触しやすさに係数を掛け合わせて表現します。
その係数のことを反応速度定数といい、正反応および逆反応のそれを \(k_1\), \(k_2\) としましょう。
すると、正反応および逆反応の反応速度 \(v_1\), \(v_2\) は次式で表されることになります。
式(8)\[ v_1 = k_1 [\text{H}_2] [\text{I}_2] \\[15pt] v_2 = k_2 [\text{HI}]^2 \]
「 \(v_2\) に関して式(7)中の \(\frac{1}{2}\) はどこに行ってしまった?」と思われるかもしれませんが、重要なのは濃度であり係数ではないため反応速度定数に吸収させてしまいました。
元は \(v_2 = \frac{1}{2}k_2' [\text{HI}]^2\) だったけど、\(k_2 = \frac{1}{2}k_2'\) にしても差し支えないでしょうということです。
こうして反応速度を導入しましたが、これが可逆反応系の説明にどのように寄与するのかを示していきます。
質量作用の法則
冒頭で説明した疑問がはるか昔のように感じられるので再度明記しておくと、
化学反応とは不可逆変化以外に可逆変化なるものが存在し、それは反応物から生成物へ変化する反応およびその逆の反応が両方常に起きている。しかしながら、身の回りに実在するものからその変化を観察できることは無いため、可逆反応系では分子レベルでどの様な状態となっているのかを明らかにしたいという事でした。
いい加減勿体ぶらずに解答を示していくと、まず可逆反応系では常に反応が起きているといっても見かけ上変化が観察されなくなる状態に落ち着くということを理解しなければなりません。
そして反応系が見かけ上変化しなくなる状況は反応速度を用いて簡潔に表現することができます。
反応速度とは物質濃度の時間変化であり、もう少し分かりやすく言うと分子が反応物から生成物、あるいはその逆に化学変化するのにどのくらいの時間を要するかを表したものでした。
以上のことから、反応系の見かけ上の変化がなくなることは正反応と逆反応の反応速度が一致して反応物と生成物の増減のバランスが取れることだと言えるでしょう。
式(9)\[ \begin{align*} v_1 &= v_2 \\[15pt] k_1 [\text{H}_2] [\text{I}_2] &= k_2 [\text{HI}]^2 \\[15pt] \Leftrightarrow ~ \frac{[\text{HI}]^2}{[\text{H}_2] [\text{I}_2]} &= \frac{k_1}{k_2} = \text{Const.} \end{align*} \]
反応系の見かけ上の変化が無くなることを「平衡状態に達した」と表現し、式(9)で得られる定数値が ( 式(2)の ) 平衡状態を記述する定数になります。
この定数は平衡定数と呼ばれ慣習的に \(K\) で表されます。
式(10)\[ K = \frac{[\text{HI}]^2}{[\text{H}_2] [\text{I}_2]} \]
また平衡状態を濃度の積によって記述することができる法則のことを「質量作用の法則」と呼びます。
この平衡定数を導入したことによる成果は、私達が反応系に手を加えて自在に操作できるようになったことです。
例えば生成物であるヨウ化水素をたくさん生成させようものなら、水素あるいはヨウ素の量を反応容器に追加すれば良いという指針を私達に与えてくれます。
それを式(10)を基に説明すると、左辺は常に一定値を取り続けるので、右辺の分子を大きくする ( 目的物を増やす ) ということは同時に分母も大きくする必要があるということを教えてくれるワケです。
また以上の内容を更に一般化して、例えば次のような可逆反応系を考えるとき
式(11)\[ a ~ \text{A} + b ~ \text{B} \cdots ~ \rightleftharpoons ~ c ~ \text{C} + d ~ \text{D} \cdots \]
その平衡定数は次にように与えられます。
式(12)\[ K = \frac{[\text{C}]^c [\text{D}]^d ~ \cdots}{[\text{A}]^a [\text{B}]^b ~ \cdots} \]
化学反応式(11)中の大文字のアルファベットが化学式を、その前に付いた小文字のアルファベットが係数を表しています。
この可逆反応系の平衡定数は、各物質に掛かる係数分だけ累乗した濃度の積を考えます。
その際、一般的に化学反応式の左辺および右辺に与えられた物質について、平衡定数にはそれぞれ分母、分子に置くのが規則となっています。
具体例を基にして帰納的に一般化された平衡定数式(12)を提示しましたが、これは熱力学の理論から導くことが可能です。
熱力学から導かれる結果では更に詳細な情報が与えられることになり、例えば当コンテンツでは触れられなかった温度に関する条件が付随してきます。
基本的には系の温度が一定であれば、平衡定数は常に一定値を取ることを理解しておけば問題ないでしょう。

