高校課程で物理選択をしていた方であれば、光が波動であることをご存知と思います。
その「光」の研究を推し進めることによって、エネルギーに最小単位があることが見いだされました。
そしてこのことが契機となり量子論の幕が開かれることになります。
これから2部に渡って光について見ていきますが、当コンテンツは光が波動であることの説明や重要な性質について学習するページになっています。
光の波動性
光の波動性を顕著に表している実験はヤングによるもので、歴史的に見ても彼の実験によって粒子説派の学者たちを驚かせた程です。
教科書的には「2重スリット実験」などと呼ばれていますね。
少し簡略化していますが実験の様子を図に示しました。
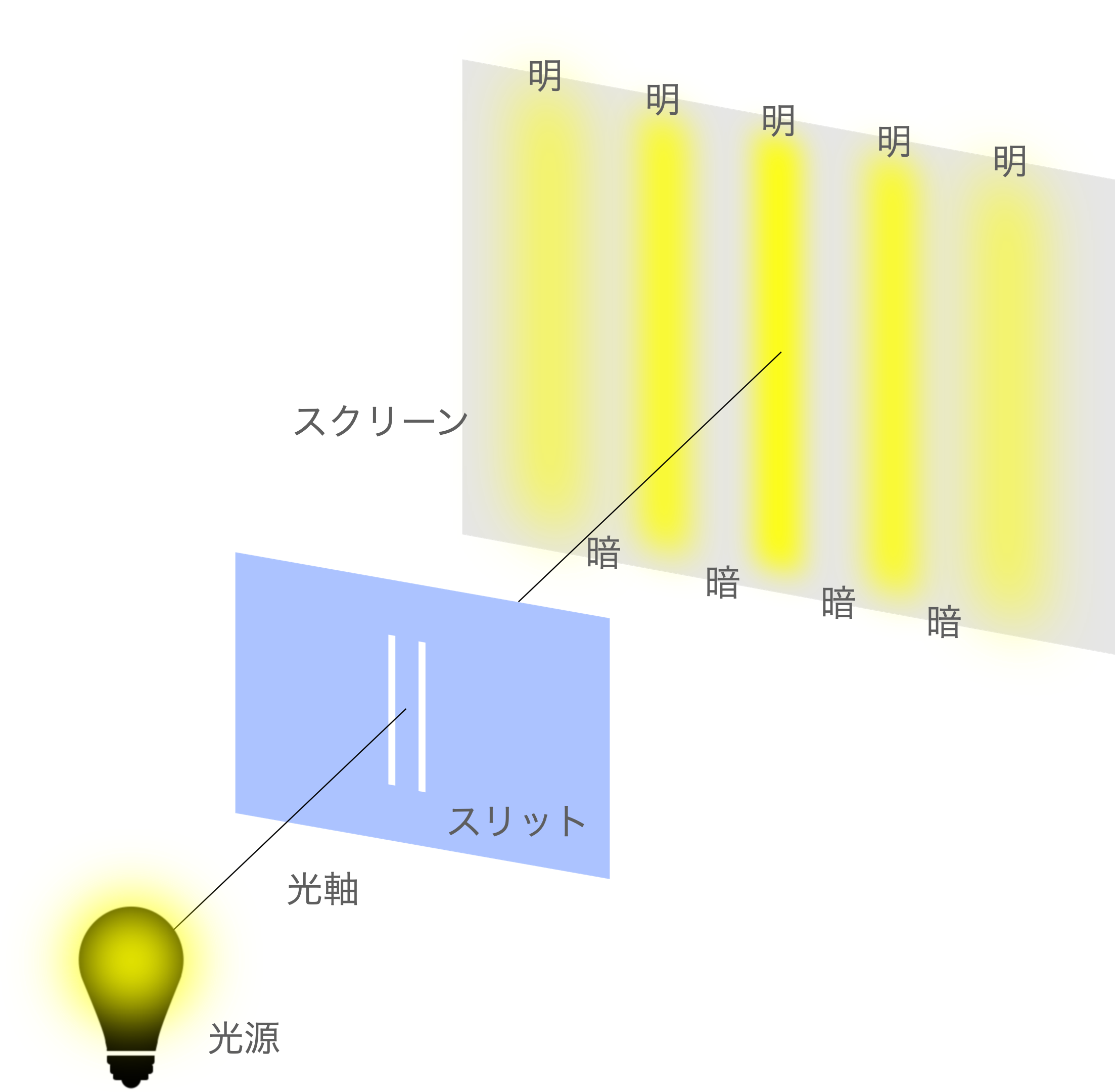
※ちなみに2重スリットの2重とは2つのスリット(穴)が空いているということであって、2つ何かが重なっているのではないので注意です。
光源から放射された光は二重スリットに到達し、それぞれのスリットを通過して出てきた光は、スクリーンに明暗の縞模様を作るように映し出されます。
この実験結果を説明するために、光は波動であると考えるとよさそうです。
もし光が粒子であれば、縞模様を作る以前に光の明部はより限定的な範囲に収まるはずだからですね。
光がスリットを抜け出たときに、粒子であるならそのまま直進すると考えられます。
つまり、光源を原点としてそこからスリットを通るような直線を考え、その直線をスクリーン上へ延長すれば粒子が衝突する位置を決定できます。
その衝突位置の数は当然2箇所になるはずで、それはスリットが2つあることから分かります。
したがって明部は2箇所存在するという予測を立てることができますね。
ところが実際、光の像は縞模様であり且つ広範囲に映し出されます。
スリットから出てきた光はそのまま直進するのではなく、スリットを抜けた後では広がりをもちながら進行しているとしか考えようがないのです。
これは光が波動であるとした場合、この現象を解釈することができます。
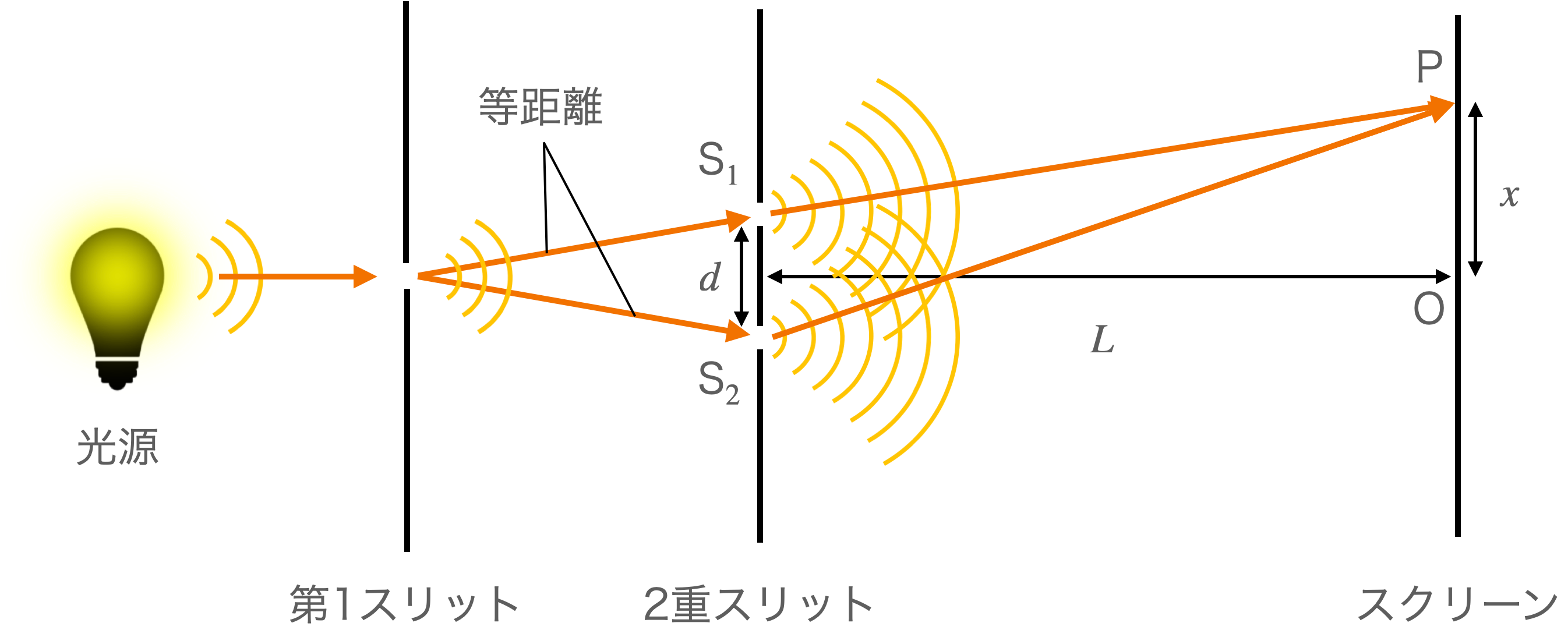
スリットから出てきた光が長さ \(L\) だけ先にあるスクリーンに到達したときに映し出される模様を考えましょう。
ただし、スクリーンは二重スリットから十分に離れているとします( \(L \gg d \) )。
2つのスリットの中点から垂直にスクリーンにおろした点をOとし、そこから \(x\) だけ離れたスクリーン上の点Pについて見ることにします。
何を考えるかというと、それぞれのスリットから出た光が点Pに到達したときに、干渉作用によって強めあっているのか、あるいは弱めあっているのかということです。
つまりそれぞれのスリットから出た光の位相を知ることができれば、点Pの明るさが分かります。
※2つの波動を考え、それらの位相が一致しているほど強めあい、位相のズレが \(\pi = 180^\circ\) に近いほど弱め合うことを思い出しましょう。
今、スリットを波源として、そこから等方的に広がる光を考えているので、スリットから距離 \(r\) だけ離れた位置における波の位相は次式で表されます。
式(1)\[ kr = \frac{2\pi}{\lambda}r \]
\(k \left(= \frac{2\pi}{\lambda}\right)\) は波数を、\(\lambda\) は波長を表し、それぞれ次元は[rad/m]、[m]です。
ここで波数の意味を次元から解釈すると、単位長さあたりに位相が進む速さを表しています。
「速さ」と表現すると波の速さと混同してしまいかねないので別の表現をすれば、長さをラジアンに換算したものと捉えておくといいでしょう。
例えば、1波長分の長さ(\( ~ 1\lambda ~ \))は \(2\pi\) と表現でき、半波長分の長さ(\( ~ 0.5\lambda ~ \))は \(\pi\) と表現できるようになります。
実際に、波数 \(k \left(= \frac{2\pi}{\lambda}\right)\) に \( ~ 1\lambda ~ \) を掛けると \(2\pi\) になり、 \( ~ 0.5\lambda ~ \) を掛けてると \(\pi\) になることが確認できます。
このように、それぞれの長さと位相が波数 \(k\) を取り持って対応していることが分かると思います。
同様に、波源から任意の長さ \(r\) だけ先の位置の位相は \(k\) に \(r\) を掛けることによって得られますね。
※また、より任意性の高い話になってくると、2地点 (\(r, r_0\)) の間の位相差を考える様になります。その際、位相差は、\(k(r-r_0)\) で表現されます。
それでは、寄り道は以上にして光の波動性に話を戻します。
まず、光を第1スリットを通過させ、続いて等距離に位置した2つのスリットS\(_1\), S\(_2\)を同時に通過させることにより、位相が揃った光がそれぞれのスリットから出てくるようにします。
※位相は \(kr\) で分かりますが、一般には \(kr + \phi\) といったように初期位相 \(\phi\) を足しておきます。ですが、今回は簡単のためにスリットから出てきた瞬間の光の位相を0とすることにします。つまり \(\phi = 0\) です。
次に、S\(_1\)P、およびS\(_2\)Pの長さを知る必要があるので、図の様に直角三角形Q\(_1\)PS\(_1\)とQ\(_2\)PS\(_2\)を考えます。
Q\(_1\)およびQ\(_2\)はスリットの位置からスクリーンに垂直におろした点であることに注意すると、|Q\(_1\)P| \(= x - \frac{d}{2}\)、|Q\(_2\)P| \(= x + \frac{d}{2}\) となります。
表記が煩雑になってくるので、\(_1\)P、およびS\(_2\)Pの長さを \(r_1\)、\(r_2\) と表現することにしましょう。
したがって、三平方の定理から \(r_1\) = |S\(_1\)P|、および \(r_2\) = |S\(_2\)P| を求めると
式(2-1)\[ \begin{align*} r_1 &= \sqrt{~L^2 + \left(x - \frac{d}{2}\right)^2} \\[10pt] &= \sqrt{~L^2 \left\{ 1 + \left(\frac{2x-d}{2L}\right)^2 \right\} } \\[10pt] &= L\sqrt{1 + \left(\frac{2x-d}{2L}\right)^2} \end{align*} \]
式(2-2)\[ \begin{align*} r_2 &= \sqrt{~L^2 + \left(x + \frac{d}{2}\right)^2} \\[10pt] &= \sqrt{~L^2 \left\{ 1 + \left(\frac{2x+d}{2L}\right)^2 \right\} } \\[10pt] &= L\sqrt{1 + \left(\frac{2x+d}{2L}\right)^2} \end{align*} \]
ここで \(\left| x \right| \ll L\) が成り立つような、なるべく光軸に近い範囲でのみ観測するとして、式(2-1)および式(2-2)をテイラー展開により近似すると、次のようになります。
式(2-1)’\[ \begin{align*} r_1 &= L\sqrt{1 + \left(\frac{2x-d}{2L}\right)^2} \\[10pt] &\simeq L \left\{ 1 + \frac{1}{2}\left(\frac{2x-d}{2L}\right)^2 \right\} \end{align*} \]
式(2-2)’\[ \begin{align*} r_2 &= L\sqrt{1 + \left(\frac{2x+d}{2L}\right)^2} \\[10pt] &\simeq L \left\{ 1 + \frac{1}{2}\left(\frac{2x+d}{2L}\right)^2 \right\} \end{align*} \]
テイラー1次近似は、\(\sqrt[\alpha]{1 + X} = (1 + X)^{\frac{1}{\alpha}} \simeq 1 + \frac{1}{\alpha}X ~ (~ \left|X\right| \ll 1 ~)\) を利用しています。
それぞれのスリットから点Pまでの距離が求まったので、各経路でどのくらい位相が進んだのか式(1)を利用して計算できますね。
スリットS1からの出た波については
式(3-1)\[ kr_1= \frac{2\pi}{\lambda} L \left\{ 1 + \frac{1}{2}\left(\frac{2x-d}{2L}\right)^2 \right\} \]
スリットS2からの出た波については
式(3-2)\[ kr_2= \frac{2\pi}{\lambda} L \left\{ 1 + \frac{1}{2}\left(\frac{2x+d}{2L}\right)^2 \right\} \]
となります。
続いて波の重ね合わせを考えて行きましょう。
そのためには、注目している点Pにおける波の高さを知る必要があります。
一般に原点から距離 \(r\) における波動の位相は式(1)の \(kr\) で表現できることを前述しましたが、その点における波の高さは \(\sin\) 関数に位相情報をそのまま放り込めばいいので、次のように表されます。
式(4)\[ y(r) = A\sin{kr} \]
ここで \(A\) は振幅を表しています。
したがって、点Pでの波の高さは、S\(_1\)から出てくる波動を\(y_1\)、S\(_2\)から出てくる波動を\(y_2\)として、これらを足し合わせればいいので
式(5)\[ \begin{align*} y_P(r_1, r_2) &\equiv y_1(r_1) + y_2(r_2) \\[10pt] &= A\sin{kr_1} + A\sin{kr_2} \\[10pt] &= A\left\{\sin{kr_1} + \sin{kr_2} \right\} \\[10pt] &=2A\sin{\frac{k(r_1 + r_2)}{2}} \cos{\frac{k(r_1 - r_2)}{2}} \end{align*} \]
となります。
最後の等号では、和積の公式 \(\sin{A} + \sin{B} = 2\sin{\frac{A + B}{2}}\cos{\frac{A - B}{2}}\) を利用しました。
ここで式(2-1)'および式(2-2)'から \(r_1\) と \(r_2\) の和と差を求めると
式(6-1)\[ r_1 + r_2 = L \left\{ 2 + \left( \frac{x}{L} \right)^2 + \frac{1}{4}\left( \frac{d}{L} \right)^2 \right\} \simeq 2L \]
式(6-2)\[ r_1 - r_2 = -\frac{d}{L}x \]
となります。
式(6-1)に関しては、\(\left|x\right| \ll L\) かつ \(d \ll L\) であることから \(\frac{x}{L}\) および \(\frac{d}{L}\) が非常に小さい数値になることが分かるので、これら微小量を無視しています。
以上から、\(y_P(r_1, r_2)\) は更に
式(7)\[ \begin{align*} y_P(r_1, r_2) &=2A\sin{\frac{k(r_1 + r_2)}{2}}\cos{\frac{k(r_1 - r_2)}{2}} \\[10pt] &= 2A\sin{kL}\cos{\frac{k}{2}\left(-\frac{d}{L}x \right)} \\[10pt] &= 2A\sin{\frac{2\pi L}{\lambda}}\cos{\frac{\pi d}{\lambda L}x} \end{align*} \]
のように変形できます。
実際にスクリーンに映し出される光の強度 \(I(x)\) は、振幅 \(y_P(r_1, r_2)\) の2乗で表されるので、
式(8)\[ \begin{align*} I(x) &= \left|y_P(x)\right|^2 \\[10pt] &= 4A^2 \sin^2{\frac{2\pi L}{\lambda}} \cos^2{\frac{\pi d}{\lambda L}x} \\[10pt] &= 4A^2 \sin^2{\frac{2\pi L}{\lambda}} \left( 1 + \cos{\frac{2\pi d}{\lambda L}x} \right) \end{align*} \]
といった表式になります。
この式(8)から \(I(x)\) は \(\cos\) で表され、明暗は \(\frac{L\lambda}{d}\) の間隔で周期的に繰り返されることが分かります。
つまり、\(I(x)\) が0になるところでは暗くなり、0以外のところで明るくなることを示し、それが周期的に現れるので縞模様として結果として映し出されるということですね。
また以下補足で別コンテンツの宣伝を載せておくことにします(興味がない方は次の節へ飛んでOK)。
先程得た式(8) \(\cos\) 関数は \(x\) に無関係に無限に続いていくので、無限遠でも光の明暗が観測できてしまうことになりますが、実際はそんなこと考えられないですよね。
これは、式(2)を式(2)'に近似する際に \(|x| \ll L\) の条件を課しましたが、つまりこれは \(x\) が光軸付近でのみ成り立つ条件なので、当然 \(x\) が \(+\infty\) となるあるいは \(-\infty\) となる範囲では成立しません。
実際には \(x\) が光軸から離れていくに従って薄暗くなってくれるのが理想です。
つまり式(8)には \(x\) が光軸から大きく離れていくのに伴なって減衰するようになっていないということですね。
当コンテンツでは詳細には触れないでおきますが、筆者が計算した結果では2重スリットによって映し出される強度分布関数は、
\[ I(x) = \frac{8h^2}{\pi^2x^2}\sin^2\frac{wx}{2}\cos^2\frac{dx}{2} \]
になります。
ただし、\(h\)、\(w\) はスリットの高さおよび幅、\(d\) はスリット間距離、\(x\) は前述まで用いた \(x\) と同様にスクリーン上の位置を表しています。
式(8)と比較すると、\(\frac{1}{x^2}\) が掛かっているため、光軸から離れていくにつれて強度が弱くなることを表現できています。
実際にグラフも描いてみました。
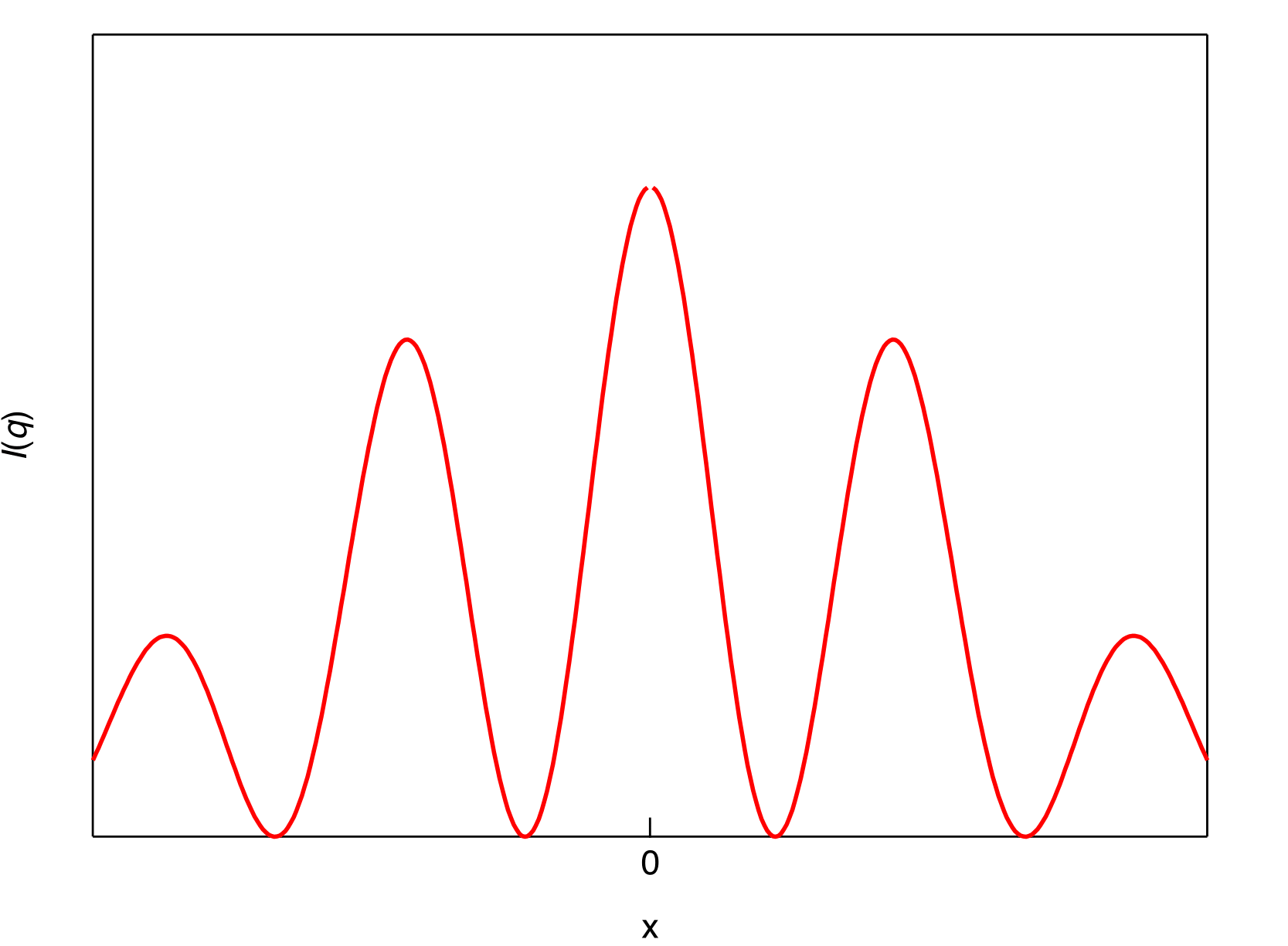
この様に、\(x\) が中心から離れるに従って減衰していく様子が視覚的にも分かります。
電磁波
現代科学において、私達が認識する光(すなわち可視光線)は電磁波の一種であることが分かっています。
そしてこの電磁波は私達の目で直接確認することはできませんが、読んで字の如く「波」として存在しています。
電磁波存在はマクスウェルによって予言され、ヘルツによって実験的に確認されましたが、この節では光が波動であるということについて説明するためにスペースを割くことにしました。
まず電磁気学においては「マクスウェル方程式」という支配方程式が存在し、これによって電磁気現象を記述・予測することができます。
ちょうど、古典力学におけるニュートンの運動方程式と同じ位置づけですね。
その支配方程式は次の4つにまとめられます。
式(9)\[ \begin{align*} &\mathrm{div}\boldsymbol{E} = \frac{\rho}{\epsilon_0} \\[10pt] &\mathrm{rot}\boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t} \\[10pt] &\mathrm{div}\boldsymbol{B} = 0 \\[10pt] &\mathrm{rot}\boldsymbol{B} = \mu_0\boldsymbol{j} + \mu_0\epsilon_0\frac{\partial \boldsymbol{E}}{\partial t} \\[10pt] \end{align*} \]
ここで、\(\boldsymbol{E}\) は電場、\(\rho\) は電荷密度、\(\boldsymbol{j}\) は電流密度、\(\boldsymbol{B}\) は磁束密度、\(t\) は時間を、また \(\epsilon\) は誘電率、\(\mu\) は透磁率であり添字0は真空下での値を表しています。
\(\mathrm{div}\) や \(\mathrm{rot}\) はベクトル量に作用する演算子で、それぞれ発散(divergence)と回転(rotation)と呼ばれるものです。
直感的には作用するベクトルがどのような向きを向いているかを表しており、発散はベクトルが四方八方に向いている様子、回転はベクトルが渦を巻いている様子を表現できて便利ですね。
※図を用意しておきます。
真空下での誘電率 \(\epsilon\) および透磁率 \(\mu\) の値定数として決まっているので提示しておくと、それぞれ
\[ \begin{align*} \epsilon_0 = 8.854 \times 10^{-12} \\[10pt] \mu_0 = 1.256 \times 10^{-6} \end{align*} \]
であり、誘電率 \(\epsilon\) の次元は[F/m]、透磁率 \(\mu\) の次元は[N/A\(^2\)]となっています。
式(9)を組み合わせて電場 \(\boldsymbol{E}\) のみの方程式および磁場 \(\boldsymbol{B}\) のみの方程式を導くことができ、1次元の場合においては
式(10)\[ \begin{align*} \frac{\partial^2\boldsymbol{E}}{\partial t^2} = \frac{1}{\mu_0\epsilon_0} \frac{\partial^2\boldsymbol{E}}{\partial x^2} \\[10pt] \frac{\partial^2\boldsymbol{B}}{\partial t^2} = \frac{1}{\mu_0\epsilon_0} \frac{\partial^2\boldsymbol{B}}{\partial x^2} \end{align*} \]
と整理できます。
ちなみに3次元では \(y\) や \(z\) の偏微分の項が足されていき \(\frac{\partial^2 E}{\partial x^2} + \frac{\partial^2 E}{\partial y^2} + \frac{\partial^2 E}{\partial z^2}\) となります、ご参考までに。
実は式(10)は波動方程式と呼ばれ、この方程式を満足する解は三角関数で与えられるのです。
つまり、ここから電場 \(\boldsymbol{E}\) や磁場 \(\boldsymbol{B}\) は波動として存在するかもしれない!?という糸口を掴んだわけですね。
また更に誘電率 \(\epsilon\) と透磁率 \(\mu\) から、面白い事に気付くことができます。
実際に次のように計算してみましょう。
式(11)\[ \frac{1}{\sqrt{\mu_0\epsilon_0}} = 2.998 \times 10^8 \]
計算した結果、次元は[m/s](速さ)になり、なんと電場と磁場に関する物理量から光の速さに非常に近しい値を得ることができるのです。
そしてこれら式(10)や式(11)の結果から、マクスウェルは電磁”波”の存在を予言し、更にその電磁波が光速で伝播することから、光も電磁波であるということを提唱するに至りました。
ここまでの話は、光が電磁波であるという予測に過ぎないのですが後年これらの基礎を元にして冒頭でもお話したようにヘルツによって電磁波の存在が実験的に確認され現在に至るわけです。
※余談ですが筆者はこの一連の流れが好きで、科学において非常に大切なことを教えてくれます。それは、実験と理論は常にセットということですね。「理論を構築できるから偉い」、「実験結果は事実なので実験が全て」、など様々な意見がありますがそれがエゴになってはいけません。

