水の沸点は標準圧力 \(P^\circ = 1 ~ [\text{atm}]\) 下で \(100 ~ [\text{℃}]\) ではありますが、異なる成分が含まれる場合それ以上の温度まで加熱しなければ沸騰しない沸点上昇を生じる事が知られています。

当ページでは沸点上昇を理論的に理解して、沸点上昇度を求めることを目的としています。

沸点と沸点上昇

液体を加熱した時、ある温度以上になると気体に状態変化する沸騰を生じます。このときの温度が沸点であり、例えば標準圧力 \(P^\circ = 1 ~ [\text{atm}]\) における水の沸点は \(100 ~ [\text{℃}]\) です。

ただし、この沸点は純粋な水における物性値であり、別の成分である食塩などが混合している場合には \(100 ~ [\text{℃}]\) を超える温度にならなければ沸騰しないことが知られており沸点上昇と呼ばれています。

沸点における系の記述

沸騰のメカニズム

液体の温度が沸点に達すると沸騰が始まります。沸騰とは、液体の内部で気泡が盛んに生じる事です。

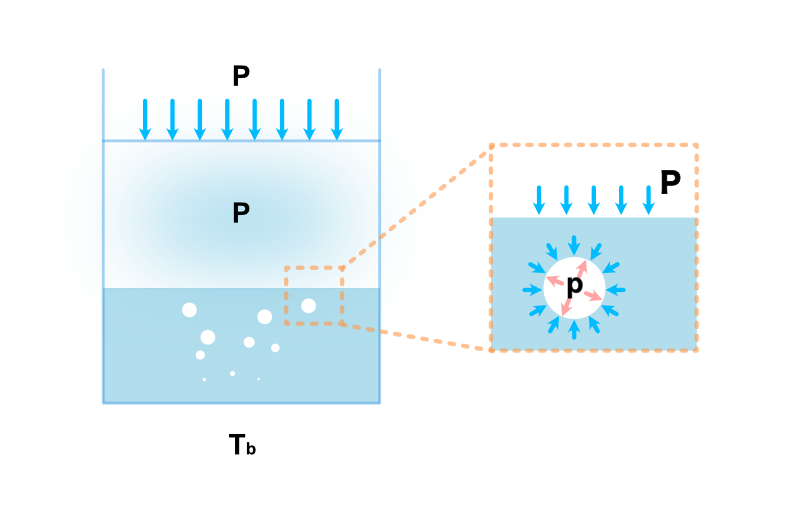
気泡内部の圧力、すなわち蒸気圧を \(p\)、系全体に加わる圧力を \(P\) としたとき

• \(p < P\) : 気泡は消滅する
• \(p \geq P\) : 気泡は消滅しない

となります。また等号成立 ( \(p = P\) ) は液体の温度が沸点 \(T_\text{b}\) に等しいときです。

化学ポテンシャルによる沸点付近の記述

化学ポテンシャルを用いて沸点付近の系の記述を考えていきます。

純粋な液体1中に気泡が消滅せずに存在するとき、次の関係式を与えることができます。

\[ \mu^{\text{(G)}}_1(T_\text{b}, ~ P) = \mu^{\text{(L)}}_1(T_\text{b}, ~ P) \]

\(\mu^{\text{(G)}}_1\) は気泡として存在する成分1の化学ポテンシャル、\(\mu^{\text{(L)}}_1\) は液体成分1の化学ポテンシャルです。

ただしそれぞれの化学ポテンシャルは、より厳密には次にように定義しておくのが良いでしょう。

\[ \begin{align*} \mu^{\text{(G)}}_1(T_\text{b}, ~ P) \equiv \lim_{\substack{T \rightarrow T_\text{b} + 0 \\[2pt] p \rightarrow P}} \mu^{\text{(G)}}_1(T, ~ p) \\[15pt] \mu^{\text{(L)}}_1(T_\text{b}, ~ P) \equiv \lim_{T \rightarrow T_\text{b} - 0} \mu^{\text{(L)}}_1(T, ~ P) \end{align*} \]

事実として、温度 \(T_\text{b}\) では、液体は激しく沸騰するため平衡状態には成り得ず、化学ポテンシャルは定義できません。

そのため着目したい状況に限りなく近づけた極限として表す必要があります。

また圧力 \(P\) の下、成分1が気体として存在できるのは \(T_\text{b}\) 以上、他方で液体として存在できるのは \(T_\text{b}\) 以下の温度領域なので、それぞれの化学ポテンシャルは片側極限値によって定めました。

つまり、\(\mu^{\text{(G)}}_1\) は高温側から \(T_\text{b}\) に限りなく近づけていった極限値、\(\mu^{\text{(L)}}_1\) は低温側から \(T_\text{b}\) に限りなく近づけていった極限値です。

沸点上昇の理論的導出

純粋な溶媒成分1に不揮発性の溶質成分2を少量添加したとき、成分1の沸点がどのように変化するのか理論的に調べていきます。

結論 溶媒成分1の沸点は上昇しますが、その事実を前提にすることなく結果を予測することも同時に確認してみましょう。

まず混合物である溶液の沸点が、純粋な溶媒と比較して異なる値を取ることを明らかにしておきます。

調製して得られた溶液を定圧下 \(P\) の下で、純粋な溶媒成分1の沸点 \(T_\text{b}\) まで加熱した場合を考えます。

仮に温度 \(T_\text{b}\) で溶液内で気泡が生じるとし、気泡と液相間のつり合いを化学ポテンシャルを用いて記述すると次式で表されます。

\[ \mu^{\text{(G)}}_1(T_\text{b}, ~ P) = \mu^{\text{(L)}}_1(T_\text{b}, ~ P; ~ \boldsymbol{n}^{\text{(L)}}) \]

ここで、式(3)左辺は純粋な気体の化学ポテンシャルを用いています。いま溶質成分2は揮発性をもたないため、ここで発生する気泡は成分1のみから構成されるためです。

式(3)右辺は混合溶液の中の成分1の化学ポテンシャルであり、理想希薄溶液では更に成分1のモル分率 \(x_1\) を用いて次のように書き換えられます。

\[ \mu^{\text{(L)}}_1(T_\text{b}, ~ P; ~ \boldsymbol{n}^{\text{(L)}}) = \mu^{\text{(L)}}_1(T_\text{b}, ~ P) + RT_\text{b} \ln x_1 \]

したがって、式(3)に式(4)を代入すると次の関係式が得られます。

\[ \mu^{\text{(G)}}_1(T_\text{b}, ~ P) = \mu^{\text{(L)}}_1(T_\text{b}, ~ P) + RT_\text{b} \ln x_1 \]

ここで式(1)から \(\mu^{\text{(G)}}_1(T_\text{b}, ~ P) = \mu^{\text{(L)}}_1(T_\text{b}, ~ P)\) が成立しているので、式(5)と合わせて考えると 結局…

\[ \begin{gather*} RT_\text{b} \ln x_1 = 0 \\[15pt] \therefore ~ x_1 = 1 \end{gather*} \]

となってしまいます。

これは純粋な溶媒であることを表しており、すなわち先に設けた仮定が誤りであったことが分かります。

つまり溶液が沸騰し始めるのは \(T_\text{b}\) から幾分かズレた \(T_\text{b} + \Delta T_\text{b}\) であるということです。

式(5)から温度を少しズラした次の関係式が、溶液が沸騰する際のつり合いの式になります。

\[ \mu^{\text{(G)}}_1(T_\text{b} + \Delta T_\text{b}, ~ P) = \mu^{\text{(L)}}_1(T_\text{b} + \Delta T_\text{b}, ~ P) + R (T_\text{b} + \Delta T_\text{b}) \ln x_1 \]

ここで現状 \(\Delta T_\text{b}\) の符号は明らかにしていません。結論として沸点は上昇するので \(\Delta T_\text{b} > 0\) となるのですが、続く内容から理解していただけるでしょう。

式(6)の化学ポテンシャルについて、温度変化に対するテイラー1次近似を行うと

\[ \begin{align*} &\mu^{\text{(G)}}_1(T_\text{b} + \Delta T_\text{b}, ~ P) \simeq \mu^{\text{(G)}}_1(T_\text{b}, ~ P) + \left( \frac{\partial \mu^{\text{(G)}}_1 (T_\text{b}, ~ P)}{\partial T} \right)_P \Delta T_\text{b} \\[15pt] &\mu^{\text{(L)}}_1(T_\text{b} + \Delta T_\text{b}, ~ P) \simeq \mu^{\text{(L)}}_1(T_\text{b}, ~ P) + \left( \frac{\partial \mu^{\text{(L)}}_1 (T_\text{b}, ~ P)}{\partial T} \right)_P \Delta T_\text{b} \end{align*} \]

であるため、式(6)に代入すると次の関係式が得られます。

\[ \mu^{\text{(G)}}_1(T_\text{b}, ~ P) + \left( \frac{\partial \mu^{\text{(G)}}_1 (T_\text{b}, ~ P)}{\partial T} \right)_P \Delta T_\text{b} ~ \simeq ~ \mu^{\text{(L)}}_1(T_\text{b}, ~ P) + \left( \frac{\partial \mu^{\text{(L)}}_1 (T_\text{b}, ~ P)}{\partial T} \right)_P \Delta T_\text{b} + R (T_\text{b} + \Delta T_\text{b}) \ln x_1 \]

式(1)から、純粋な成分1の化学ポテンシャルは両辺から消滅するので

\[ \left( \frac{\partial \mu^{\text{(G)}}_1 (T_\text{b}, ~ P)}{\partial T} \right)_P \Delta T_\text{b} ~ \simeq ~ \left( \frac{\partial \mu^{\text{(L)}}_1 (T_\text{b}, ~ P)}{\partial T} \right)_P \Delta T_\text{b} + R (T_\text{b} + \Delta T_\text{b}) \ln x_1 \]

となります。

化学ポテンシャルの温度に関する偏微分係数はモルエントロピーに等しく \(\left( \frac{\partial \mu}{\partial T} \right)_P = -\bar{S}\) が成立することを考慮して、式(8)を整理していくと

\[ \begin{align*} &\text{eq(9.1) :} ~~~~~ -\bar{S}^{\text{(G)}}_1(T_\text{b}, ~ P) ~ \Delta T_\text{b} ~ \simeq ~ -\bar{S}^{\text{(L)}}_1(T_\text{b}, ~ P) ~ \Delta T_\text{b} + R (T_\text{b} + \Delta T_\text{b}) \ln x_1 \\[15pt] &\text{eq(9.2) :} ~~~~~ - \left\{ \Delta \bar{S}_\text{v}(T_\text{b}, ~ P) + R \ln x_1 \right\} \Delta T_\text{b} ~ \simeq ~ RT_\text{b} \ln x_1 \\[15pt] &\text{eq(9.3) :} ~~~~~ \therefore ~ \Delta T_\text{b} \simeq -\frac{RT_\text{b} \ln x_1}{\Delta \bar{S}_\text{v}(T_\text{b}, ~ P) + R \ln x_1} \end{align*} \]

ここで \(\Delta \bar{S}_\text{v}\) は蒸発エントロピー変化で、定義は次のとおりです。

\[ \Delta \bar{S}_\text{v}(T_\text{b}, ~ P) \equiv \bar{S}^{\text{(G)}}_1(T_\text{b}, ~ P) - \bar{S}^{\text{(L)}}_1(T_\text{b}, ~ P) \]

更に近似して式(9.3)を整えていきます。

\(\ln x_1\) を含む項に着目すると、式(9.3)右辺分母の \(R \ln x_1\) は \(\Delta S_\text{v}\) と比較して小さく無視できることに気が付きます。実際トルートンの規則によると \(\Delta S_\text{v} \simeq 88 ~ [\text{J/mol･K}]\) であり、対して \(R \ln x_1 \simeq 0 ~ \left( ~ \because ~ x_1 \rightarrow 1 ~ \right)\) です。

また式(9.3)右辺分子 \(\ln x_1\) について

\[ \ln x_1 = \ln (1 - x_2) \simeq -x_2 ~~~ ( ~ \because x_2 \rightarrow 0 ~ ) \]

と近似できます。

これらの事から式(9.3)は次のように書き換えることができます。

\[ \Delta T_\text{b} \simeq \frac{RT_\text{b}}{\Delta \bar{S}_\text{v}(T_\text{b}, ~ P)} x_2 > 0 \]

式(12)右辺は正の値を取るので、このことから \(\Delta T_\text{b} > 0\) となり異なる成分の混合によって沸点が上昇することが導かれます。

また蒸発エントロピー変化は、蒸発エンタルピー変化 \(\Delta \bar{H}_\text{v}\) を用いて \(\bar{S}_\text{v} = \frac{\bar{H}_\text{v}}{T_\text{b}}\) で表されるので、式(12)は次のようになります。

\[ \Delta T_\text{b} \simeq \frac{RT^2_\text{b}}{\Delta \bar{H}_\text{v}(T_\text{b}, ~ P)} x_2 \]