純粋な溶媒に溶質を加えていったとき、溶媒の蒸気圧は純粋な状態における蒸気圧と比較して小さくなる事が知られています。これを蒸気圧降下と言います。

当ページでは、不揮発性の溶質を添加した場合を例に、溶媒の蒸気圧がどの様な挙動を示すのか理論的な説明を与えることが目標です。

蒸気圧降下とは

蒸気圧が \(P^*_1\) である純粋な溶媒1に不揮発性の溶質2を添加したとき、溶媒の蒸気圧は \(P_1 < P^*_1\) となって小さくなることが知られています。

この現象は蒸気圧降下と呼ばれます。

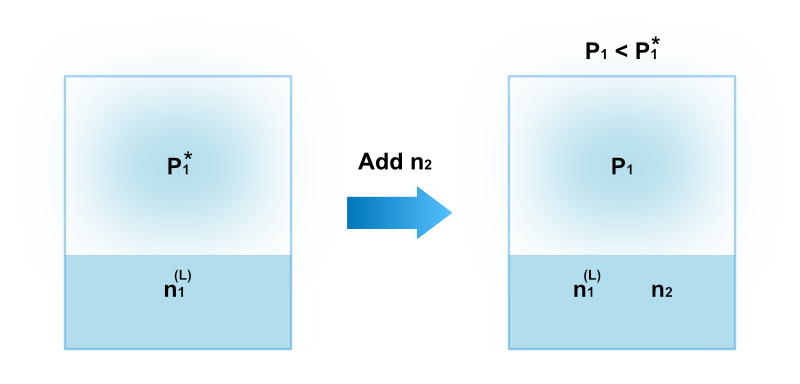
以下、なぜ蒸気圧降下が生じるのか、熱力学的な視点から考えていきます。

蒸気圧降下の理論的説明

一般的な説明

蒸気圧降下の理論的説明は一般にラウールの法則が利用されます。

揮発性溶媒1に対して、不揮発性の溶質2を少量添加する場合を考えましょう。

溶質2が少量であれば溶媒1に対して次式に示すラウールの法則が近似的に成立します。

\[ P_1 = P^*_1 x_1 \]

• \(P_1\) : 溶媒1の蒸気圧
• \(P^*_1\) : 純粋な溶媒1の蒸気圧
• \(x_1\) : 溶媒1のモル分率

式(1)について、溶媒1のモル分率 \(x_1\) を溶質2のモル分率 \(x_2\) に置き換えます。すると…

\[ \begin{align*} &P_1 = P^*_1 (1 - x_2) \\[15pt] &P^*_1 - P_1 = P^*_1 x_2 \\[15pt] \therefore ~ &\Delta P = P^*_1 x_2 ~~~ ( ~ \Delta P \equiv P^*_1 - P_1 ~ ) \end{align*} \]

この様に蒸気圧降下度 \(\Delta P\) を定めることができ、それは溶質2のモル分率 \(x_2\) に比例する関係が得られます。

ただし、前述の通り式(2)はラウールの法則が成立する条件の下であることに注意しましょう。

拡張した理論

前項の内容は一般に蒸気圧降下を理論的に示す説明です。

しかし溶媒の蒸気圧の挙動は、少量の溶質を添加した場合に限定されていました。

そこで、より一般的な関係式が得られないか計算してみようという試みを行おうと思います。

揮発性溶媒1と不揮発性溶質2からなる溶液と、溶媒1の蒸気が気液平衡状態にあるとします。

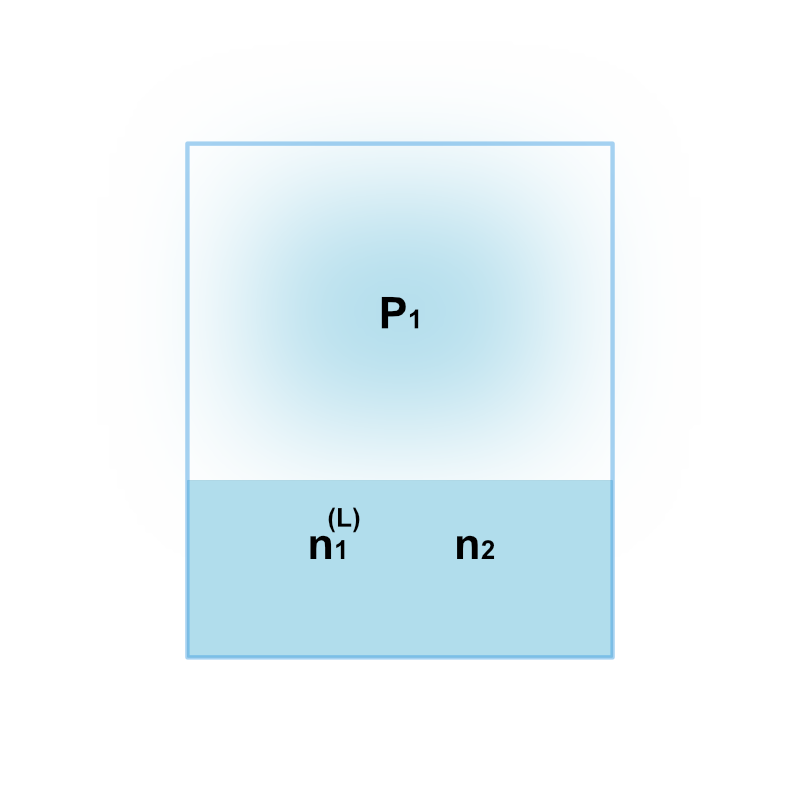
このとき平衡条件から、液相と気相の溶媒1の化学ポテンシャルが等しいので次式が成立します。

\[ \mu^{\text{(L)}}_1(T, ~ P_1; ~ n^{\text{(L)}}_1, ~ n_2) = \mu^{\text{(G)}}_1(T, ~ P_1) \]

添字の1, 2はそれぞれ溶媒1および溶質2の物理量をであることを示します。また液相か気相かを明示する必要がある物理量には、それぞれ(L), (G)を添えています。

この状態から更に溶質2を添加すると、系は別の平衡状態に移るので次のように記述できます。

\[ \mu^{\text{(L)}}_1(T, ~ P_1 + dP_1; ~ n^{\text{(L)}}_1 + dn^{\text{(L)}}_1, ~ n_2 + dn_2) = \mu^{\text{(G)}}_1(T, ~ P_1 + dP_1) \]

系は等温環境下に置かれているとして温度の変化は考えません。

式(4)両辺のテイラー1次近似は次の通り

\[ \mu^{\text{(L)}}_1(T, ~ P_1 + dP_1; ~ n^{\text{(L)}}_1 + dn^{\text{(L)}}_1, ~ n_2 + dn_2) = \mu^{\text{(L)}}_1(T, ~ P_1; ~ n^{\text{(L)}}_1, ~ n_2) + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial P_1} \right)_{T, ~ n^{\text{(L)}}_1, ~ n_2} dP_1 + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n^{\text{(L)}}_1} \right)_{T, ~ P_1, ~ n_2} dn^{\text{(L)}}_1 + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n_2} \right)_{T, ~ P_1, ~ n^{\text{(L)}}_1} dn_2 \]

\[ \mu^{\text{(G)}}_1(T, ~ P_1 + dP_1) = \mu^{\text{(G)}}_1(T, ~ P_1) + \left( \frac{\partial \mu^{\text{(G)}}_1}{\partial P_1} \right)_T dP_1 \]

したがって、式(4)は次のように展開されます。

\[ \mu^{\text{(L)}}_1(T, ~ P_1; ~ n^{\text{(L)}}_1, ~ n_2) + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial P_1} \right)_{T, ~ n^{\text{(L)}}_1, ~ n_2} dP_1 + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n^{\text{(L)}}_1} \right)_{T, ~ P_1, ~ n_2} dn^{\text{(L)}}_1 + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n_2} \right)_{T, ~ P_1, ~ n^{\text{(L)}}_1} dn_2 = \mu^{\text{(G)}}_1(T, ~ P_1) + \left( \frac{\partial \mu^{\text{(G)}}_1}{\partial P_1} \right)_T dP_1 \]

また式(5)から式(3)を引いて整理すると次式が得られます。

\[ \left\{ \left( \frac{\partial \mu^{\text{(G)}}_1}{\partial P_1} \right)_T - \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial P_1} \right)_{T, ~ n^{\text{(L)}}_1, ~ n_2} \right\} dP_1 = \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n^{\text{(L)}}_1} \right)_{T, ~ P_1, ~ n_2} dn^{\text{(L)}}_1 + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n_2} \right)_{T, ~ P_1, ~ n^{\text{(L)}}_1} dn_2 \]

化学ポテンシャルの圧力に関する偏微分係数はその成分の部分モル体積に等しく、更にモル体積 \(\bar{V}\) と大差が無いとすると式(6)から次式になります。

\[ \left( \bar{V}^{\text{(G)}}_1 - \bar{V}^{\text{(L)}}_1 \right) dP_1 = \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n^{\text{(L)}}_1} \right)_{T, ~ P_1, ~ n_2} dn^{\text{(L)}}_1 + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n_2} \right)_{T, ~ P_1, ~ n^{\text{(L)}}_1} dn_2 \]

ここで圧力変化 \(dP_1\) および溶液中の溶媒成分の物質量変化 \(dn^{\text{(L)}}_1\) は、溶質2の添加 \(dn_2\) によって生じた変化です。

要するに、これらは独立に振る舞うのではなく次に示すように \(n_2\) に関する偏微分係数を用いて記述することができます。

\[ \begin{align*} dP_1 &= \left( \frac{\partial P_1}{\partial n_2} \right)_{T} dn_2 \\[15pt] dn^{\text{(L)}}_1 &= \left( \frac{\partial n^{\text{(L)}}_1}{\partial n_2} \right)_{T} dn_2 \end{align*} \]

したがって、式(7)に代入して整理すると次式が導かれます。

\[ \begin{align*} &\text{eq(9.1) :} ~~~~~ \left( \bar{V}^{\text{(G)}}_1 - \bar{V}^{\text{(L)}}_1 \right) \left( \frac{\partial P_1}{\partial n_2} \right)_{T} dn_2 = \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n^{\text{(L)}}_1} \right)_{T, ~ P_1, ~ n_2} \left( \frac{\partial n^{\text{(L)}}_1}{\partial n_2} \right)_{T} dn_2 + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n_2} \right)_{T, ~ P_1, ~ n^{\text{(L)}}_1} dn_2 \\[30pt] &\text{eq(9.2) :} ~~~~~ \Rightarrow ~ \left( \bar{V}^{\text{(G)}}_1 - \bar{V}^{\text{(L)}}_1 \right) \left( \frac{\partial P_1}{\partial n_2} \right)_{T} = \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n^{\text{(L)}}_1} \right)_{T, ~ P_1, ~ n_2} \left( \frac{\partial n^{\text{(L)}}_1}{\partial n_2} \right)_{T} + \left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n_2} \right)_{T, ~ P_1, ~ n^{\text{(L)}}_1} \end{align*} \]

最後に式(9)から、溶質を少量添加した場合において蒸気圧降下の現象を説明できるか確認してみましょう。

溶質を少量だけ添加するとき、溶媒の化学ポテンシャルは溶媒のモル分率を用いて次式で与えられます。

\[ \begin{align*} \mu^{\text{(L)}}_1(T, ~ P_1; ~ dn^{\text{(L)}}_1, ~ n_2) &= \mu^{\text{(L)}}_1(T, ~ P_1) + RT \ln x_1 \\[15pt] &= \mu^{\text{(L)}}_1(T, ~ P_1) + RT \ln \frac{n^{\text{(L)}}_1}{n^{\text{(L)}}_1 + n_2} \end{align*} \]

物質量に関する偏微分係数を求めると

\[ \begin{align*} &\left( \frac{\partial \mu^{\text{(L)}}}{\partial n^{\text{(L)}}_1} \right)_{T, ~ P_1, ~ n_2} = \frac{n_2 RT}{n^{\text{(L)}}_1 (n^{\text{(L)}}_1 + n_2)} \\[15pt] &\left( \frac{\partial \mu^{\text{(L)}}_1}{\partial n_2} \right)_{T, ~ P_1, ~ n^{\text{(L)}}_1} = -\frac{RT}{n^{\text{(L)}}_1 + n_2} \end{align*} \]

となるので、式(9.2)に代入して整理すると次式が得られます。

\[ \left( \bar{V}^{\text{(G)}}_1 - \bar{V}^{\text{(L)}}_1 \right) \left( \frac{\partial P_1}{\partial n_2} \right)_{T} = \frac{RT}{n^{\text{(L)}}_1 + n_2} \left\{ \frac{n_2}{n^{\text{(L)}}_1} \left( \frac{\partial n^{\text{(L)}}_1}{\partial n_2} \right)_{T} - 1 \right\} \]

いま、溶質2の添加量は少量であるため \(\frac{n_2}{n^{\text{(L)}}_1} \ll 1\) であり、かつ溶質2の添加による溶媒1の物質量変化も \(\left( \frac{\partial n^{\text{(L)}}_1}{\partial n_2} \right)_{T} \simeq 0\) と無視できるとすれば式(12)は簡単になります。

\[ \left( \bar{V}^{\text{(G)}}_1 - \bar{V}^{\text{(L)}}_1 \right) \left( \frac{\partial P_1}{\partial n_2} \right)_{T} = -\frac{RT}{n^{\text{(L)}}_1 + n_2} \]

更にモル体積について、一般に液体よりも気体のほうが非常に大きく \(\left( \bar{V}^{\text{(G)}}_1 \gg \bar{V}^{\text{(L)}}_1 \right)\)、液体のモル体積の寄与を無視すると

\[ \bar{V}^{\text{(G)}}_1 \left( \frac{\partial P_1}{\partial n_2} \right)_{T} = -\frac{RT}{n^{\text{(L)}}_1 + n_2} \]

となります。

気体のモル体積 \(\bar{V}^{\text{(G)}}_1 = \frac{RT}{P_1}\) を代入すると

\[ \frac{1}{P_1} \left( \frac{\partial P_1}{\partial n_2} \right)_{T} = -\frac{1}{n^{\text{(L)}}_1 + n_2} \]

が得られます。

\(\left( \frac{\partial P_1}{\partial n_2} \right)_{T} < 0\) であることは明らかで、式(15)は蒸気圧降下を表した関係に他なりません。

また式(15)を変形したものと、式(2)と比較をしてみましょう。

\[ \begin{align*} \text{eq(2) :} ~~~~~ &P^*_1 - P_1 = P^*_1 x_2 ~ && \Leftrightarrow ~ \frac{P_1 - P^*_1}{P^*_1} = - x_2 \\[15pt] \text{eq(15) :} ~~~~~ &\frac{1}{P_1} \left( \frac{\partial P_1}{\partial n_2} \right)_{T} = -\frac{1}{n^{\text{(L)}}_1 + n_2} ~ && \Leftrightarrow ~ \frac{dP_1}{P_1} = - \frac{dn_2}{n^{\text{(L)}}_1 + n_2} \end{align*} \]

少々表式は異なるものの、それぞれ圧力変化と溶質モル分率の変化の関係を表している事は理解できます。