液体成分の化学ポテンシャル

液体や溶液中に存在する成分の化学ポテンシャルは、気液平衡状態にある蒸気の化学ポテンシャルから間接的に求めることができます。

備忘録としてまとめておきます。

純粋な液体成分の化学ポテンシャル

液体とその蒸気のみが存在する系において気液平衡状態にあるとき、液体成分の化学ポテンシャル \(\mu^{\text{(L)}}\) とその蒸気の化学ポテンシャル \(\mu^{\text{(G)}}\) は等しい値を取ります。

系の温度が \(T\)、蒸気圧が \(P^*\) であるとき、平衡条件は次式で与えられます。

\[ \mu^{\text{(L)}}(T, ~ P^*) = \mu^{\text{(G)}}(T, ~ P^*) \]

また気体の化学ポテンシャルは、圧力依存性から任意の圧力を基準とした表示に書き換えることができます。

例えば標準圧力 \(P^\circ\) を基準とすると \(\mu^{\text{(G)}}(T, ~ P^*)\) は

\[ \mu^{\text{(G)}}(T, ~ P^*) = \mu^{\text{(G)}}(T, ~ P^\circ) + RT \ln \frac{P^*}{P^\circ} \]

と書くことができます。

したがって、純粋な液体成分の化学ポテンシャル \(\mu^{\text{(L)}}(T, ~ P^*)\) も結局 次式となります。

\[ \mu^{\text{(L)}}(T, ~ P^*) = \mu^{\text{(G)}}(T, ~ P^\circ) + RT \ln \frac{P^*}{P^\circ} \]

溶液中の成分の化学ポテンシャル

溶液中に存在する成分 \(i\) の化学ポテンシャルはどのように記述できるでしょうか。

これも気液平衡状態にある溶液中の成分 \(i\) とその蒸気の化学ポテンシャルが等しくなることを用いれば分かります。

いま系の温度が \(T\)、気相の全圧を \(P\) としたとき次式が成立します。

\[ \mu^{\text{(L)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(L)}}) = \mu^{\text{(G)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(G)}}) \]

混合気体中の成分 \(i\) の化学ポテンシャルはその分圧 \(P_i\) を用いて

\[ \mu^{\text{(G)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(G)}}) = \mu^{\text{(G)}}_i(T, ~ P) + RT \ln \frac{P_i}{P} \]

と表すことができるので、式(4), (5)から溶液中の成分 \(i\) の化学ポテンシャルが次式になることが分かります。

\[ \mu^{\text{(L)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(L)}}) = \mu^{\text{(G)}}_i(T, ~ P) + RT \ln \frac{P_i}{P} \]

更に、気体の化学ポテンシャルの圧力依存性から、式(6)右辺の圧力を \(P \rightarrow P^*_i\) ( : 純粋な成分 \(i\) の蒸気圧 ) にしたものが次式です。

\[ \mu^{\text{(L)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(L)}}) = \mu^{\text{(G)}}_i(T, ~ P^*_i) + RT \ln \frac{P_i}{P^*_i} \]

式(1)で示すように、純粋な成分では液体とその蒸気の化学ポテンシャルは等しく \(\mu^{\text{(G)}}_i(T, ~ P^*_i) = \mu^{\text{(L)}}_i(T, ~ P^*_i)\) が成立するので、結果として導かれる溶液中の成分 \(i\) の化学ポテンシャルは次式になります。

\[ \mu^{\text{(L)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(L)}}) = \mu^{\text{(L)}}_i(T, ~ P^*_i) + RT \ln \frac{P_i}{P^*_i} \]

実は溶液中の成分 \(i\) の化学ポテンシャルは次式で記述されることもあります。

\[ \mu^{\text{(L)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(L)}}) = \mu^{\text{(L)}}_i(T, ~ \textcolor{red}{P}) + RT \ln \frac{P_i}{P^*_i} \]

要するに、1成分の化学ポテンシャルでは圧力変数として純粋な状態における蒸気圧 \(P^*_i\) ではなく、系の全圧 \(P\) を用いても良いということです。

式(9)は液体の化学ポテンシャルの圧力依存性が小さいという結論から近似的に導かれますが、更にそれは成分 \(i\) の蒸気圧が全圧 \(P\) の影響をほとんど受けないことに等しいです。

例えば温度 \(T\)、圧力 \(P^*_i\) で気液平衡状態にある純粋な成分 \(i\) が封入された容器に空気を混合する状況を考えます。

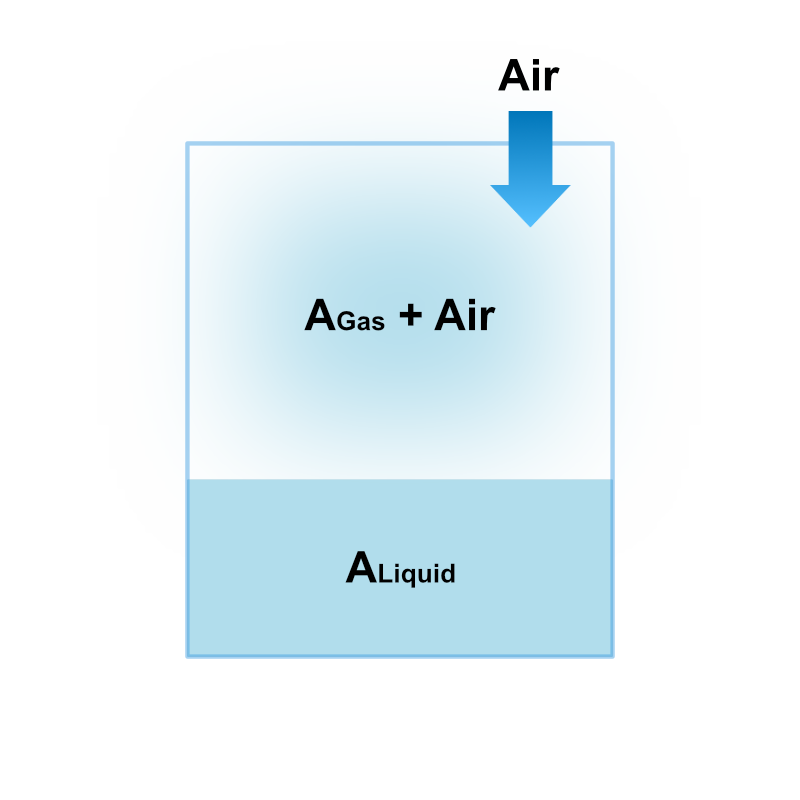
事実この混合操作によって成分 \(i\) の気液平衡状態は純粋なときと比較して変化しており、蒸気圧は \(P^*_i\) から \(P_i\) ( : 空気と混合された気体の分圧 ) となります。

しかしながら蒸気圧の変化は非常に小さく、異なる気体成分の存在は着目している成分の蒸気圧にほとんど影響を及ぼさないことが導かれます。

詳細は蒸気圧の測定を解説したページに譲りますが、要するに

\[ P_i \simeq P^*_i \]

が成立するということです。

またこのとき、先に示した容器内の成分 \(i\) について空気を混合した後の平衡条件を考えると次の通り。

\[ \mu^{\text{(L)}}_i(T, ~ P) = \mu^{\text{(G)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(G)}}) \]

ただし空気は液相に溶解しないと仮定して、式(11)左辺には純粋な液体成分 \(i\) の化学ポテンシャルを用いました。

式(11)右辺は成分 \(i\) の分圧 \(P_i\) を用いて

\[ \mu^{\text{(G)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(G)}}) = \mu^{\text{(G)}}_i(T, ~ P) + RT \ln \frac{P_i}{P} \]

圧力依存性から基準を蒸気圧 \(P^*_i\) にとれば次式になります。

\[ \mu^{\text{(G)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(G)}}) = \mu^{\text{(G)}}_i(T, ~ P^*_i) + RT \ln \frac{P_i}{P^*_i} \]

前述の通り、成分 \(i\) の分圧は混合前の純粋状態における蒸気圧 \(P^*_i\) からほとんど変化せず、式(10)によって式(13)の対数項は消滅し次の近似が得られます。

\[ \mu^{\text{(G)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(G)}}) \simeq \mu^{\text{(G)}}_i(T, ~ P^*_i) \]

式(14)を式(11)と組み合わせることによって

\[ \mu^{\text{(L)}}_i(T, ~ P) \simeq \mu^{\text{(G)}}_i(T, ~ P^*_i) \]

が得られ、式(1)で示す通り純粋な成分の化学ポテンシャルは液体とその蒸気で共に等しいので、式(15)右辺を液体の化学ポテンシャルで置き換えると

\[ \mu^{\text{(L)}}_i(T, ~ P) \simeq \mu^{\text{(L)}}_i(T, ~ P^*_i) \]

となります。

したがって、式(16)の近似によって式(8)から直ちに式(9)が導けることが分かるでしょう。

\[ \begin{align*} &\text{eq(8) :} ~~~~~ \mu^{\text{(L)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(L)}}) = \mu^{\text{(L)}}_i(T, ~ P^*_i) + RT \ln \frac{P_i}{P^*_i} \\[15pt] &\text{eq(9) :} ~~~~~ \Rightarrow ~ \mu^{\text{(L)}}_i(T, ~ P; ~ \boldsymbol{n}^{\text{(L)}}) = \mu^{\text{(L)}}_i(T, ~ P) + RT \ln \frac{P_i}{P^*_i} \end{align*} \]