ブラウン運動とは、分子や粒子の運動様式のことであり、発見した人に因んでその様に呼ばれています。

基本的に系を構成する分子や粒子はアボガドロ数個にも及び、分子1つ1つの運動を追いかける事は困難を極めます。

そのため統計力学の体系では系を構成する分子全体の統計的性質について議論が行われます。

しかしある1分子に着目し、その他の分子から受ける影響を確率的に扱うことで着目分子の平均的な挙動を記述することが可能になります。

ブラウン運動とは

ブラウン運動とは、分子の運動様式のことです。

無数の分子から構成された系について、分子1つ1つの運動を追いかける事は困難ですが、確率論的に1分子の運動を記述することは可能です。

ある1分子について運動方程式を考えましょう。

上記の様子は次のように記述できます。

\[ m\frac{d\boldsymbol{v}(t)}{dt} = \boldsymbol{F} - \zeta \boldsymbol{v}(t) + \boldsymbol{R}(t) \]

• \(m\) : 着目している分子の質量
• \(t\) : 時刻
• \(\boldsymbol{v}(t)\) : 着目している分子の速度ベクトル
• \(\boldsymbol{F}\) : 着目している分子に働く力
• \(\zeta\) : 抵抗係数
• \(\boldsymbol{R}(t)\) : 着目している分子に働くランダム力

\(\boldsymbol{F}\) は分子に働く力で重力などが上げられます。

\(\zeta \boldsymbol{v}(t)\) は着目分子の運動が妨げられるように働く抵抗力です。抵抗によって着目分子は減速させられるので負号を付けています。

最後に \(\boldsymbol{R}(t)\) のランダム力は周りの分子との衝突から受ける力であり、確率的に様々な向き・大きさを取り得ます。

ブラウン運動で要点となるのはランダム力 \(\boldsymbol{R}(t)\) であり、これをどの様に解析していくか問題となります。

ブラウン運動する分子の解析

ブラウン運動を記述する運動方程式(1)を解析的に解いていきましょう。

方針としては

• 分子の速度ベクトル \(\boldsymbol{v}(t)\) を求める
• 速度ベクトルの平均について考える
• 分子の位置ベクトル \(\boldsymbol{r}(t)\) を求める
• 位置ベクトルの平均について考える

この順序で内容を展開していきます。

ブラウン運動する分子の速度ベクトル

いま着目している分子の質量は非常に小さいので力 \(\boldsymbol{F}\) は 0 であるとします。

それによって式(1)を書き換えた次式はランジュバン方程式と呼ばれたりしています。

\[ m\frac{d\boldsymbol{v}(t)}{dt} = - \zeta \boldsymbol{v}(t) + \boldsymbol{R}(t) \]

式(2)は \( \boldsymbol{R}(t) = \boldsymbol{0}\) とすれば同次解が求まる定数変化法を用いる事ができます。

実際には…

\[ \begin{align*} &m\frac{d\boldsymbol{v}(t)}{dt} = - \zeta \boldsymbol{v}(t) \\[15pt] \Leftrightarrow ~~~ & \frac{d\boldsymbol{v}(t)}{dt} = - \frac{\zeta}{m} \boldsymbol{v}(t) \end{align*} \]

といった微分方程式を初めに解くという事です。

求める関数がベクトルではない場合、例えば

\[ \frac{dA}{dt} = kA \]

このような型式の微分方程式のは \(A(t) = C e^{kt} ~ \big( ~ C \text{ : Const.} ~ \big)\) を解に持つことを参考として、式(3)の解を次のように置きます。

\[ \boldsymbol{v}(t) = \boldsymbol{C} e^{\lambda t} \]

この式(4)が同次解になります。ここで \(\boldsymbol{C}\) は定数ベクトルです。

定数変化法では得られた同次解を再度元の微分方程式に代入して解析を進めます。

ただしその際の注意点として一般に式(4)は元の微分方程式(2)の解とはならないので、その差を埋め合わせるために式(4)の定数ベクトルを \(t\) の関数 \(\boldsymbol{C}(t)\) と置き直して扱う必要があります。

つまり式(4)を \(\boldsymbol{v}(t) = \boldsymbol{C}(t) e^{\lambda t}\) として式(2)へ代入するという事です。

\[ \begin{align*} \text{eq(2) : } ~~~ m\frac{d\boldsymbol{v}(t)}{dt} &= - \zeta \boldsymbol{v}(t) + \boldsymbol{R}(t) \\[15pt] \Leftrightarrow ~ m\frac{d}{dt} \boldsymbol{C}(t) e^{-\frac{\zeta}{m}t} &= - \zeta \boldsymbol{C}(t) e^{-\frac{\zeta}{m}t} + \boldsymbol{R}(t) \end{align*} \]

式(5)左辺の微分は

\[ \frac{d}{dt} \boldsymbol{C}(t) e^{-\frac{\zeta}{m}t} = \frac{d \boldsymbol{C}(t)}{dt} \cdot e^{-\frac{\zeta}{m}t} - \frac{\zeta}{m} \boldsymbol{C}(t) e^{-\frac{\zeta}{m}t} \]

となることに注意して計算を進めると式(5)は

\[ \begin{align*} m e^{-\frac{\zeta}{m}t} \frac{d \boldsymbol{C}(t)}{dt} - \zeta \boldsymbol{C}(t) e^{-\frac{\zeta}{m}t} &= - \zeta \boldsymbol{C}(t) e^{-\frac{\zeta}{m}t} + \boldsymbol{R}(t) \\[15pt] \therefore ~ m e^{-\frac{\zeta}{m}t} \frac{d \boldsymbol{C}(t)}{dt} &= \boldsymbol{R}(t) \end{align*} \]

となります。

両辺時刻について \([0,~ t]\) の間で積分すれば \(\boldsymbol{C}(t)\) が得られますが、計算時には積分変数を形式的に \(t'\) としておきましょう。

実際の計算は次のようになります。

\[ \begin{gather*} \begin{align*} \text{eq(6) : } ~~~ m e^{-\frac{\zeta}{m}t'} \frac{d \boldsymbol{C}(t')}{dt'} &= \boldsymbol{R}(t') \\[15pt] \Leftrightarrow ~ d \boldsymbol{C}(t') &= \frac{1}{m} \boldsymbol{R}(t') e^{\frac{\zeta}{m}t'} dt' \\[15pt] \int_0^t d \boldsymbol{C}(t') &= \frac{1}{m} \int_0^t \boldsymbol{R}(t') e^{\frac{\zeta}{m}t'} dt' \\[30pt] \end{align*} \\ \therefore ~ \boldsymbol{C}(t) = \frac{1}{m} \int_0^t \boldsymbol{R}(t') e^{\frac{\zeta}{m}t'} dt' ~~~ \big( ~ \boldsymbol{C}(0) = \boldsymbol{0} ~ \big) \end{gather*} \]

ただし時刻 0 における定数ベクトル \(\boldsymbol{C}(0)\) は \(\boldsymbol{0}\) と仮定しました。

式(7)を \(\boldsymbol{v}(t) = \boldsymbol{C}(t) e^{\lambda t}\) に戻せば、結果として速度ベクトルが次式で与えられる事が分かります。

\[ \boldsymbol{v}(t) = \frac{e^{-\frac{\zeta}{m}t}}{m} \int_0^{t} \boldsymbol{R}(t') e^{\frac{\zeta}{m}t'} dt' \]

ブラウン運動する分子の平均速度

速度ベクトルは式(8)で表される通りランダム力 \(\boldsymbol{R}(t)\) によって決定されます。

ランダム力はある時刻である方向に向いていた状態から次の瞬間全く別の方向に向きが変化します。

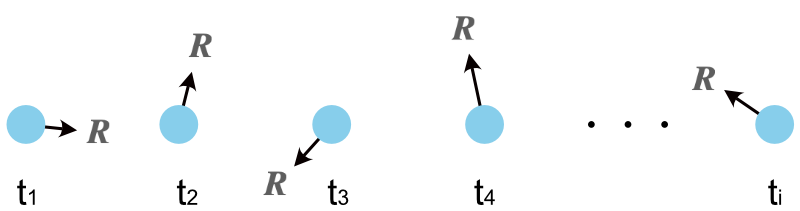
これに伴って速度ベクトルも時々刻々とランダムな方向を指すことが想定されるでしょう。

このように不規則に動く分子のある時刻における速度ベクトルをピンポイントで知ることは難しく、平均してどれくらいの量になるかを見積もるのが最適です。

結論から示すと、速度ベクトルの平均は \(\boldsymbol{0}\) となります。

それは先の図で示した通り時間変化するランダム力を足して平均を取れば \(\boldsymbol{0}\) になる事が想定されるからです。

つまりランダム力のアンサンブル平均を \(\braket{\boldsymbol{R}(t)}\) とすれば

\[ \braket{\boldsymbol{R}(t)} = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{i = 0}^N \boldsymbol{R}(t) = \boldsymbol{0} \]

が成立しており、同様に速度ベクトルについても平均を考えると

\[ \begin{align*} \braket{\boldsymbol{v}} &= \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{i = 0}^N \boldsymbol{v}(t) \\[15pt] &= \frac{e^{-\frac{\zeta}{m}t}}{m} \int_0^{t} \braket{\boldsymbol{R}(t')} e^{\frac{\zeta}{m}t'} dt' = \boldsymbol{0} ~~~ \big( ~ \because ~ \braket{\boldsymbol{R}(t')} = \boldsymbol{0} ~ \big) \end{align*} \]

といったように \(\boldsymbol{0}\) になる事が分かります。

確率的に変化する量の平均を考えるとき、2乗平均が使われることが多いです。

先で示した速度ベクトルは不規則に向きが変化するために平均が 0 となってしまいました。

それは速度成分が正の値や負の値など様々にとり得るために、全体で合計したときに 0 になることが原因だからです。

一方で2乗平均は正の値のみの平均量であるため、必ず 0 以上になります。

では、まずは2乗速度を計算してみましょう。

ベクトルの2乗は内積で与えられることに注意して

\[ \boldsymbol{v}^2 = \boldsymbol{v} \cdot \boldsymbol{v} = \left( \frac{e^{-\frac{\zeta}{m}t}}{m} \int_0^{t} \boldsymbol{R}(t') e^{\frac{\zeta}{m}t'} dt' \right) \cdot \left( \frac{e^{-\frac{\zeta}{m}t}}{m} \int_0^{t} \boldsymbol{R}(t'') e^{\frac{\zeta}{m}t''} dt'' \right) \\[15pt] = \frac{e^{-\frac{2\zeta}{m}t}}{m^2} \int_0^{t} \int_0^{t} \big( \boldsymbol{R}(t') \cdot \boldsymbol{R}(t'') \big) e^{\frac{\zeta}{m}(t' + t'')} dt' dt'' \]

となり、ここでアンサンブル平均 \(\braket{\boldsymbol{v}^2}\) を考えると

\[ \braket{\boldsymbol{v}^2} = \frac{e^{-\frac{2\zeta}{m}t}}{m^2} \int_0^{t} \int_0^{t} \braket{\boldsymbol{R}(t') \cdot \boldsymbol{R}(t'')} e^{\frac{\zeta}{m}(t' + t'')} dt' dt'' \]

を得ることができます。

さて、ここで問題になるのは式(12)に含まれるランダム力の内積の平均 \(\braket{\boldsymbol{R}(t') \cdot \boldsymbol{R}(t'')}\) です。

具体的に表したものが次になるのですが…

\[ \begin{align*} \braket{\boldsymbol{R}(t') \cdot \boldsymbol{R}(t'')} &= \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{i = 1}^N \boldsymbol{R}(t') \cdot \boldsymbol{R}(t'') \\[15pt] &= \lim_{T \rightarrow \infty} \frac{1}{T} \sum_{t' = 0}^T \boldsymbol{R}(t') \cdot \boldsymbol{R}(t' + \tau) \Delta t' ~~~ \left( ~ \begin{align*} T &= N \Delta t' \\ \tau &= t'' - t' \end{align*} ~ \right) \end{align*} \]

ここで、アンサンブル平均と時間平均が等しいと仮定して \(T = N \Delta t'\) による置き換えを行いました。この関係は時刻 0 から \(T\) まで \(\Delta t'\) の間隔で \(N\) 個の対象を測定することを表しています。

また \(\tau\) は \(t'\) と \(t''\) のズレを表します。

重要な事は式(13)が \(\boldsymbol{R}(t')\) の自己相関になっている事であり、時刻が \(\tau\) だけ変化したときの自身 \(\boldsymbol{R}(t' + \tau)\) とを比較してどのくらい類似しているかを教えてくれます。

\(\boldsymbol{R}(t)\) は非常に不規則な時間変化をするため、\(\tau\) だけズレた自身とも相関は無いと考えるのが無難です。

一方で \(\tau = 0\) つまり \(t' = t''\) のとき、つまり \(\braket{\boldsymbol{R}(t') \cdot \boldsymbol{R}(t')}\) は時刻 \(t'\) における自分自身との比較を表しますが、類似どころか全く同じものなのでピッタリ一致しているワケです。

したがってランダム力の自己相関は次のように書くことができるでしょう。

\[ \begin{align*} \braket{\boldsymbol{R}(t') \cdot \boldsymbol{R}(t' + \tau)} &= \left\{ \begin{align*} & ~ 0 && \big( ~ \tau ~ \char`≠ ~ 0 ~ \Leftrightarrow ~ t' ~ \char`≠ ~ t'' ~ \big) \\ & ~ k && \big( ~ \tau = 0 ~ \Leftrightarrow ~ t' = t'' ~ \big) \end{align*} \right. \\[20pt] &= k \delta(\tau) = k \delta(t' - t'') \end{align*} \]

\(\delta(t' - t'')\) はデルタ関数と呼ばれ、引数 \(t' - t''\) が 0 になる、すなわち \(t' = t''\) になるとき以外は 0 になる特殊な関数です。

式(14)を式(12)に代入して2乗平均速度の計算を進めると

\[ \begin{align*} \braket{\boldsymbol{v}^2} &= \frac{e^{-\frac{2\zeta}{m}t}}{m^2} \int_0^{t} \int_0^{t} k \delta(t' - t'') e^{\frac{\zeta}{m}(t' + t'')} dt' dt'' \\[15pt] &= \frac{e^{-\frac{2\zeta}{m}t}}{m^2} k \int_0^{t} \left( \int_0^{t} \delta(t' - t'') e^{\frac{\zeta}{m}(t' + t'')} dt'' \right) dt' \\[15pt] &= \frac{e^{-\frac{2\zeta}{m}t}}{m^2} k \int_0^{t} e^{\frac{2\zeta}{m}t'} dt' \\[15pt] &= \frac{e^{-\frac{2\zeta}{m}t}}{2\zeta m} k ( e^{\frac{2\zeta}{m}t} - 1 ) \\[15pt] &= \frac{1}{2\zeta m} k ( 1 - e^{-\frac{2\zeta}{m}t} ) \end{align*} \]

が得られます。

ランダム力由来の定数 \(k\) ですが、これは系の平衡状態について考えていけば具体的に明らかにすることができます。

平衡状態とは、熱力学的には十分に長い時間経過したときに系が見かけ上変化しない状態のことを言います。

\(t \rightarrow \infty\) のとき式(15)で表される2乗平均速度は指数項が 0 に近づくので

\[ \braket{\boldsymbol{v}^2} = \frac{k}{2\zeta m} ~~~ \big( ~ t \rightarrow \infty ~ \big) \]

となりますが、統計力学から導かれる結果として分子の2乗平均速度は

\[ \braket{\boldsymbol{v}^2} = \frac{3k_\text{B}T}{m} \]

で与えられるので、これらから直ちに定数 \(k\) が次のように表されることが分かります。

\[ k = 6 \zeta k_\text{B}T \]

したがって、2乗平均速度も最終的に次式で表される事になります。

\[ \braket{\boldsymbol{v}^2} = \frac{3k_\text{B}T}{m} ( 1 - e^{-\frac{2\zeta}{m}t} ) \]

またランダム力の自己相関についても次式で表される事になります。

\[ \braket{\boldsymbol{R}(t') \cdot \boldsymbol{R}(t'')} = 6 \zeta k_\text{B}T \delta(t' - t'') \]

※上述の内容では平衡状態を表現するのに \(t \rightarrow \infty\) の状況を考えましたが、理屈上は式(15)の指数項が 0 と見なせる時間だけ置けば良いと言えます。その時間を緩和時間と呼び、時間減衰する関数 \(e^{-\frac{t}{\tau}}\) について時間 \(t\) の係数の逆数 \(\tau\) で与えられます。ただしこの緩和時間 \(\tau\) は本編中に現れる時刻のズレ \(\tau\) とは全く別物であることに注意。ブラウン運動の解析から得られる指数項について緩和時間を考えると、平衡状態に達するまでに必要な時間は概ね \(\frac{m}{\zeta}\) となる事が分かります。

ブラウン運動する分子の位置ベクトル

分子の位置 \(\boldsymbol{r}(t)\) はどの様に表されるでしょうか。

位置ベクトル \(\boldsymbol{r}(t)\) は、速度ベクトルを時間で積分すれば求めることができて

\[ \begin{align*} \boldsymbol{r}(t) &= \int_0^t \boldsymbol{v}(t') dt' \\[15pt] &= \int_0^t \left( \frac{e^{-\frac{\zeta}{m}t'}}{m} \int_0^{t'} \boldsymbol{R}(t'') e^{\frac{\zeta}{m}t''} dt'' \right) dt' \end{align*} \]

となります。

また式(21)は積分区間を変換することによって更に計算ができます。

いま積分変数 \(t'\) と \(t''\) は \(0 \leq t' \leq t\) かつ \(0 \leq t'' \leq t'\) の領域で動くことが可能であり、\(t'\) - \(t''\) グラフで示すと次図のようになります。

この領域は \(t'' \leq t' \leq t\) かつ \(0 \leq t'' \leq t\) と表すこともでき、つまり \(t'\) と \(t''\) の積分区間を次のように変更しても問題ありません。

\[ \int_0^t \left( \frac{e^{-\frac{\zeta}{m}t'}}{m} \int_0^{t'} \boldsymbol{R}(t'') e^{\frac{\zeta}{m}t''} dt'' \right) dt' = \int_{\textcolor{red}{t''}}^{\textcolor{red}{t}} \left( \frac{e^{-\frac{\zeta}{m}t'}}{m} \int_{\textcolor{red}{0}}^{\textcolor{red}{t}} \boldsymbol{R}(t'') e^{\frac{\zeta}{m}t''} dt'' \right) dt' \]

この積分区間の変換は次に示すように、領域を縦に割ったか、横に割ったかの違いだけです。

式(22)右辺の計算を進めると

\[ \begin{align*} &\int_{t''}^t \left( \frac{e^{-\frac{\zeta}{m}t'}}{m} \int_0^{t} \boldsymbol{R}(t'') e^{\frac{\zeta}{m}t''} dt'' \right) dt' \\[15pt] &= \int_0^t \boldsymbol{R}(t'') e^{\frac{\zeta}{m}t''} \left( \int_{t''}^t \frac{e^{-\frac{\zeta}{m}t'}}{m} dt' \right) dt'' \\[15pt] &= \int_0^t \boldsymbol{R}(t'') e^{\frac{\zeta}{m}t''} \left\{ \frac{1}{\zeta} ( e^{-\frac{\zeta}{m}t''} - e^{-\frac{\zeta}{m}t} ) \right\} dt'' \\[15pt] &= \frac{1}{\zeta} \int_0^t \boldsymbol{R}(t'') \left\{ 1 - e^{\frac{\zeta}{m}(t'' - t)} \right\} dt'' \\[20pt] \therefore ~ & \boldsymbol{r}(t) = \frac{1}{\zeta} \int_0^t \boldsymbol{R}(t') \left\{ 1 - e^{\frac{\zeta}{m}(t' - t)} \right\} dt' \end{align*} \]

を得ることができます。

最後、積分変数を形式的に \(t''\) から \(t'\) に置き換えていることに注意してください。

ブラウン運動する分子の平均変位量

位置ベクトルの平均を考えてみましょう。

式(23)で表されるように位置ベクトルも確率的に決まる量なので、速度の平均 \(\braket{\boldsymbol{v}}\) が \(\boldsymbol{0}\) であるのと同様に \(\braket{\boldsymbol{r}}\) も \(\boldsymbol{0}\) となります。

そこで分子の位置についても2乗平均 \(\braket{\boldsymbol{r}^2}\) を求める事にします。

まず位置ベクトルの2乗を求める必要があり、それは次に示すように内積によって得られます。

\[ \begin{align*} \boldsymbol{r}^2 = \boldsymbol{r} \cdot \boldsymbol{r} &= \left[ \frac{1}{\zeta} \int_0^t \boldsymbol{R}(t') \left\{ 1 - e^{\frac{\zeta}{m}(t' - t)} \right\} dt' \right] \cdot \left[ \frac{1}{\zeta} \int_0^t \boldsymbol{R}(t'') \left\{ 1 - e^{\frac{\zeta}{m}(t'' - t)} \right\} dt'' \right]\\[15pt] &= \frac{1}{\zeta^2} \int_0^t \int_0^t \big( \boldsymbol{R}(t') \cdot \boldsymbol{R}(t'') \big) \left\{ 1 - e^{\frac{\zeta}{m}(t'' - t)} \right\} \left\{ 1 - e^{\frac{\zeta}{m}(t' - t)} \right\} dt' dt'' \end{align*} \]

続けて位置ベクトルの2乗についてアンサンブル平均を計算していきます。

その際、前述したランダム力の自己相関が現れるので式(20)を用いて計算を進めると

\[ \begin{align*} \braket{\boldsymbol{r}^2} &= \frac{1}{\zeta^2} \int_0^t \int_0^t \braket{\boldsymbol{R}(t') \cdot \boldsymbol{R}(t'')} \left\{ 1 - e^{\frac{\zeta}{m}(t'' - t)} \right\} \left\{ 1 - e^{\frac{\zeta}{m}(t' - t)} \right\} dt' dt'' \\[15pt] &= \frac{6k_\text{B}T}{\zeta} \int_0^t \int_0^t \delta(t' - t'') \left\{ 1 - e^{\frac{\zeta}{m}(t'' - t)} \right\} \left\{ 1 - e^{\frac{\zeta}{m}(t' - t)} \right\} dt' dt'' ~~~ \big( ~ \braket{\boldsymbol{R}(t') \cdot \boldsymbol{R}(t'')} = 6 \zeta k_\text{B}T \delta(t' - t'') ~ \big)\\[15pt] &= \frac{6k_\text{B}T}{\zeta} \int_0^t \left\{ 1 - e^{\frac{\zeta}{m}(t' - t)} \right\}^2 dt' \\[15pt] &= \frac{6k_\text{B}T}{\zeta} \int_0^t \left\{ 1 - e^{\frac{\zeta}{m}(t' - t)} \right\}^2 dt' \\[15pt] &= \frac{6k_\text{B}T}{\zeta} \left( t - \frac{3m}{2\zeta} - \frac{m}{2\zeta} e^{-\frac{2\zeta}{m}t} + \frac{2m}{\zeta} e^{-\frac{\zeta}{m}t} \right) \end{align*} \]

となります。

\(t \rightarrow \infty\) とすると指数項は 0 に近づき、また定数項 \(\frac{3m}{2\zeta} \big( \ll t ~ \big)\) は無視されるので、結果として次式を得ることができます。

\[ \braket{\boldsymbol{r}^2} \simeq \frac{6k_\text{B}T}{\zeta}t ~~~ \big( ~ t \rightarrow \infty ~ \big) \]

このようにブラウン運動する分子では、具体的な分子の軌道を明らかにすることは困難なものの、平均的にどのくらい分子が移動するかを記述することができます。

式(26)によると、初期時刻 0 から \(t ~ [\text{s}]\) 経った後、分子は初期位置から \(\sqrt{\frac{6k_\text{B}T}{\zeta}t}\) ほど移動していると期待できるワケですね。

また \(\frac{k_\text{B}T}{\zeta}\) を新たに \(D\) と定め、拡散係数として扱われることも理解しておきたい内容です。

\[ D \equiv \frac{k_\text{B}T}{\zeta} \]

拡散係数は次元に \([\text{m}^2/\text{s}]\) を持ちます。単位時間あたりの2次元的拡がりを表し、拡散という名称が与えられることにも納得が行くことでしょう。