系を構成する分子はそれぞれ異なるの状態にあり、様々なエネルギーを持ちます。

これを微視的状態 ( ミクロな状態 ) と言って、熱力学で議論される系の巨視的状態 ( マクロな状態 ) と対比されて用いられます。

当ページでは統計力学の議論において重要となる微視的状態の考え方について解説します。

微視的状態の考え方

微視的状態とは、系を構成する分子がそれぞれどの様な状況にあるかを表したものです。

一方で熱力学で用いられる巨視的状態という用語がありますが、これは系全体の状態を温度、体積、物質量 \((T; ~ V, ~ n)\) などの変数の組を用いて表します。

熱力学では分子の存在を仮定せずとも成立する理論体系であり、全体として平均的な状態を記述する分には非常に強力な理論となります。

しかしミクロ視点で系を観察したとき、それぞれの分子が全く同じ状態にあるのではなく異なる状態を取っているのです。

それぞれの分子が異なる状態にあることを、エネルギーの違いによって記述していきます。

具体的には、系の総エネルギー \(E\) をそれぞれの分子に分配することになります。

例えば次の図に示すようなエネルギーの大きさがラベルされた箱があるとしましょう。

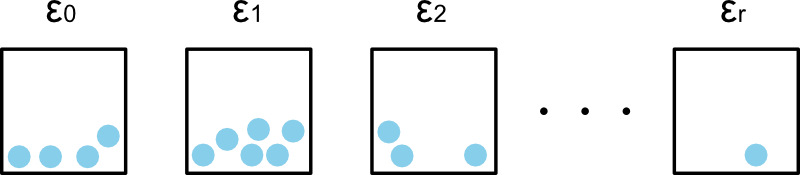
ある分子のエネルギーを観測して \(\left[\epsilon_i - \frac{\Delta \epsilon}{2}, ~ \epsilon_i + \frac{\Delta \epsilon}{2}\right]\) 間にあるとき、その分子を \(\epsilon_i\) の箱に入れる…といった具合で分配していきます。

ただし、分配の仕方には以下の条件が付与されることに注意しなければなりません。

エネルギー \(\epsilon_0\), \(\epsilon_1\), \(\epsilon_2\) \(\cdots\) \(\epsilon_r\) の箱に \(N_0\), \(N_1\), \(N_2\) \(\cdots\) \(N_r\) 個の分子が入っていれば、系の総エネルギーは

\[ N_0 \epsilon_0 + N_1 \epsilon_1 + N_2 \epsilon_2 + \cdots + N_r \epsilon_r = \sum_{i = 0}^r N_i \epsilon_i \]

と表されますが、当然これは分配前の系の総エネルギー \(E\) と一致する必要があります。

\[ E = \sum_{i = 0}^r N_i \epsilon_i \]

更に分子数について、分子は破壊したりしない限りその総数 \(N\) は一定なので

\[ N = \sum_{i = 0}^r N_i \]

を満たします。

これら式(2)および式(3)の束縛条件を考慮に入れて、分子の分配を考える必要があります。

微視的状態の場合の数

前節で微視的状態の考え方として、エネルギーの異なる箱に分子を分配する方法を示しました。

次に考えることは、この分配の仕方を数学的に表現することです。

それには \(r\) 個の箱に \(N\) 個の分子を分配する組み合わせの数を考えれば良いことが分かります。

その組み合わせの総数を \(w\) とすると次のように記述できます。

\[ w(N_0, ~ N_1, ~ \cdots ~ N_r) = \frac{N!}{N_0! N_1! \cdots N_r!} = \frac{N!}{\prod_{i = 0}^r N_i!} \]

式(4)がそれぞれの箱に分子が \((N_0, ~ N_1, ~ \cdots ~ N_r)\) という組み合わせで分配された場合の微視的状態の総数となります。

ここで、式(4)は区別可能なものを分ける際に利用できる事を思い出しましょう。

例えば簡単のために、2つの分子A, Bを2つの箱1, 2に分ける場合を考えると下記の4状態を取り得ることが分かります。

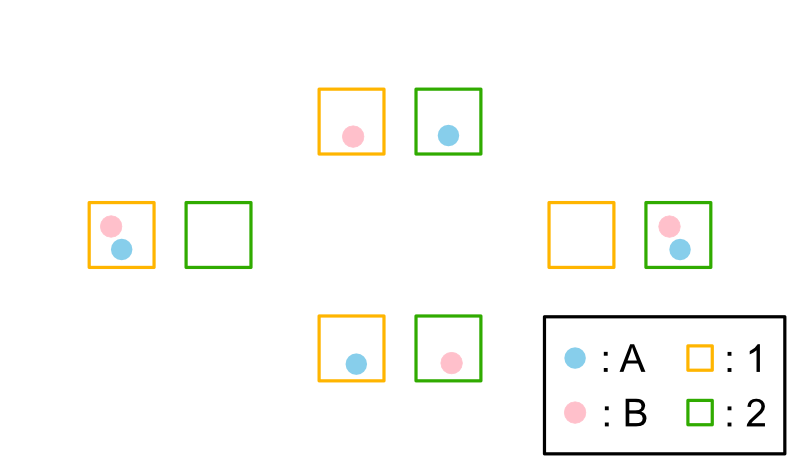
本来分子は区別できませんが、区別のある数え方をしなければ

• 箱1のみに分子が入っている場合
• 箱2のみに分子が入っている場合
• 両方の箱に分子が入っている場合

の3つの場合が均等に生じやすいことになってしまうでしょう。

実際に2つのボールと2つの箱を用意して同時にボールを箱に投げ入れたとき、両方の箱に入る場合が最も起こりやすいとは思わないでしょうか。

確率的に発生する微視的状態

ここまでに、系の微視的状態とは系を構成するそれぞれの分子がどのくらいのエネルギーを持つかを考えたものである事を示し、その微視的状態の総数も数学的に与えてきました。

以降では簡単な例を通して微視的状態を具体的に理解することに努めましょう。

またそのとき明らかとなりますが、系の総エネルギーが等しい微視的状態は複数現れることが分かります。

そして系はそれらの微視的状態の中から最も起こり得る確率が高い状態を選択します。

微視的状態の発生確率

では、微視的状態の発生確率はどのように表せば良いでしょうか。

微視的状態の数 \(w\) は、分子の分配の仕方 \((N_0, ~ N_1 ~ \cdots ~ N_r)\) によって決まることを式(3)で示しました。以降この分子数の組を \(\boldsymbol{N}\) のように書くことにします。

また分子の分配の仕方全ては以下の通りで

\[ \left\{ \begin{align*} &&(N, && 0, && 0 && \cdots && 0) \\[8pt] &&(N - 1, && 1, && 0 && \cdots && 0) \\[8pt] &&(N - 1, && 0, && 1 && \cdots && 0) \\[8pt] && && &&\vdots \\[8pt] &&(0, && 0, && 0 && \cdots && N) \end{align*} ~~~ \right\} \equiv G \]

これらの集合を \(G\) とすると、分子の分配の仕方 \(\boldsymbol{N}\) は集合 \(G\) の要素として \(\boldsymbol{N} \in G\) と表せます。

余談ですが… \(G\) の要素数は \(N\) 個の分子を \(r + 1\) 個の箱に分配する場合の数となるので

\[ {}_{N + r}\text{C}_r = \frac{(N + r)!}{N!r!} \]

ですね。

そして分子の分配の仕方 \(\boldsymbol{N}\) を \(G\) の全要素の場合について和を考えたものを \(w_{\text{toal}}\) として次のように表します。

\[ w_\text{total} = \sum_{\boldsymbol{N} \in G} w(\boldsymbol{N}) \]

以上から分子の分配 \(\boldsymbol{N}\) が発生する確率は、その場合の数 \(w(\boldsymbol{N})\) を全体事象の数で割れば良いので

\[ P(\boldsymbol{N}) = \frac{w(\boldsymbol{N})}{w_\text{total}} \]

と表されることが分かります。

微視的状態の簡単な例

単純な場合を想定して、微視的状態について理解していきます。

例えば、分子5つ、箱4個の状況を考えましょう。

それぞれの箱について、エネルギーを小さい順に並べたとき \(k\) 番目の箱のエネルギー \(\epsilon_k\) は
\((k + 1)\epsilon ~ \big( ~ 0 \leq k \leq 3 ~ \big)\) であるとします。

\[ \epsilon_k = (k + 1)\epsilon \]

ここで \(\epsilon\) は定数で、分子が取り得る最小のエネルギーです。

系の総エネルギーが \(E = 10\epsilon\) であったとき、それぞれの分子はどの箱に入ることができるでしょうか。

その組み合わせと確率を計算して以下の表にまとめました。

\(\boldsymbol{N} = (N_0, ~ N_1, ~ N_2, ~ N_3)\)	場合の数 \(w(\boldsymbol{N})\)	確率 \(P(\boldsymbol{N})\)
\((0, ~ 5, ~ 0, ~ 0)\)	\(\frac{5!}{0!5!0!0!} = 1\)	\(\sim 1\text{％}\)
\((3, ~ 0, ~ 1, ~ 1)\)	\(\frac{5!}{3!0!1!1!} = 20\)	\(\sim 20\text{％}\)
\((1, ~ 3, ~ 1, ~ 0)\)	\(\frac{5!}{1!3!1!0!} = 20\)	\(\sim 20\text{％}\)
\((2, ~ 1, ~ 2, ~ 0)\)	\(\frac{5!}{2!1!2!0!} = 30\)	\(\sim 30\text{％}\)
\((2, ~ 2, ~ 0, ~ 1)\)	\(\frac{5!}{2!2!0!1!} = 30\)	\(\sim 30\text{％}\)

\(w_\text{total} = 101\) なので、おおよそ \(\simeq 100\) として確率を計算しています。

計算結果から、どの状態が起こりやすいか分かります。

特徴としては、なるべく分子が異なる箱に分散している方が発生確率が高いと言えます。