分子の実在性

すべての物質が原子から構成されている事は現代において一般的事実として知られてはいるものの、原子の存在がどのように示されたかについて触れられる事は筆者が知る限りでは少ないです。

まして原子・分子を主に扱っていく化学の学術書ですら、それに関する説明が十分に成されているとは言えないでしょう。

そこで当ページで、原子・分子が実験的にどの様に発見されたのか簡単に触れることにします。

ペランの実験

原子・分子は目視で確認することは不可能ですが、実験的に原子・分子の存在を確認する方法を編み出したのはフランスの物理化学者ペランでした。

ペランは様々な精密実験を行うことでアボガドロ数 \(N_\text{A}\) を求めました。

その1つは、顕微鏡下で観測可能な大きさに調製した微粒子を適当な液体に分散させ、次のブラウン運動理論に沿って直接測定した平均二乗変位 \(\braket{x^2}\) からアボガドロ定数 \(N_\text{A}\) を求める方法です。

\[ \braket{x^2} = \frac{RT}{3\pi\eta r N_\text{A}} \]

ここで \(\eta ~ [\text{Pa/s}^{-1}]\) は液体の粘土、\(r ~ [m]\) は微粒子の半径です。

式(1)はブラウン運動を理論的に解析して得られる次の式

\[ \braket{\boldsymbol{r}^2} = \frac{6k_\text{B}T}{\zeta} \]

にストークスの法則から得られる抵抗係数 \(\zeta = 6\pi\eta r\) およびボルツマン定数 \(k_\text{B} = \frac{R}{N_\text{A}}\) を代入したものです。

ペランは鉛直方向に長い容器を利用して沈降平衡に達した微粒の分布からもアボガドロ定数を求めることに成功しています。

大きさが均一な微粒子を適当な液体の入った容器に加えて長時間置くと、容器の上方ほど微粒子の密度が低く下方ほど密度が高い分布をもった平衡状態に達します。

そしてペランは大胆にも顕微鏡で観察可能な大きさの微粒子にも浸透圧の理論を適用できるのではないかと考えて、実験的にその正当性を示しました。

つまり、温度 \(T ~ [\text{K}]\) のもと体積 \(V ~ [\text{m}^3]\) の液体中に存在する微粒子の数 \(n ~ [\text{mol}]\) を測定すれば、その浸透圧 \(\Pi ~ [\text{Pa}]\) が次のファント・ホッフの式で与えられるということです。

\[ \Pi V = nRT \]

微粒子が式(2)に従うことから、鉛直方向に長い容器内に生じる微粒子の密度分布を求めることができます。

容器底面を高さ 0 として、高さ \(h\) の断面付近を拡大したものが次の図です。

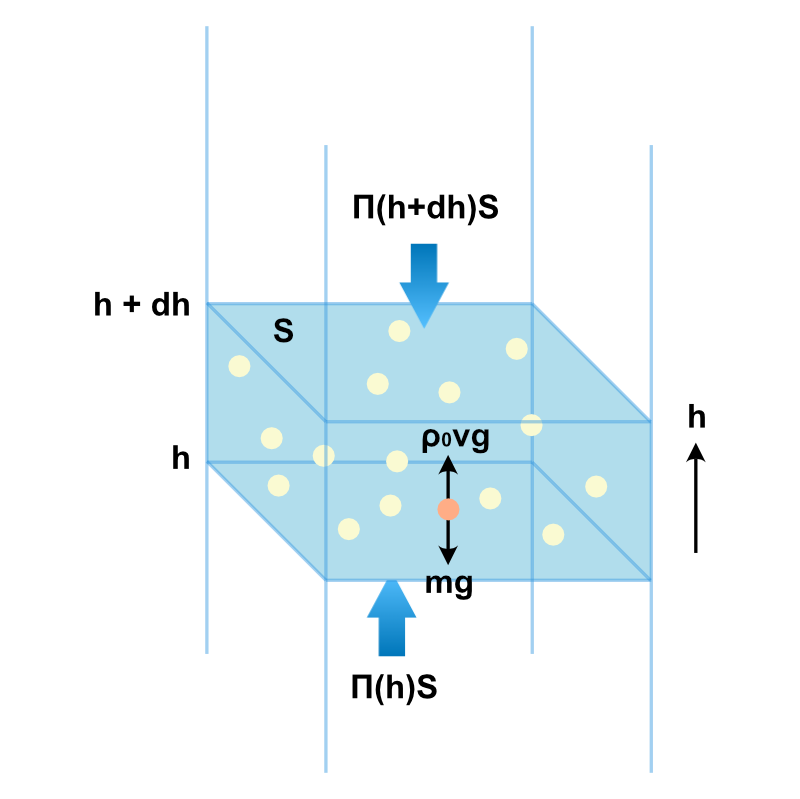
この面より上側は微粒子の密度が低いため浸透圧は小さく、逆に面よりも下側は微粒子の密度が高いため浸透圧が大きくなります。

高さ \(h\) における浸透圧を \(\Pi(h)\)としたとき、例えばそこから少しだけ高い \(h + dh\) における浸透圧との大小関係は \(\Pi(h) > \Pi(h + dh)\) となります。

このとき \(h\) から \(h + dh\) の間に存在する \(N(h)\) 個の微粒子には、上下方向からの浸透圧に容器の断面積 \(S\) を掛けた \(\Pi(h)S\) および \(\Pi(h + dh)S\) の力が平均して及ぼされます。

その他にも、微粒子の質量を \(m\)、体積を \(v\) としたとき鉛直下向きに重力 \(mg\)、密度 \(\rho_0\) の液体から受ける鉛直上向きの浮力 \(\rho_0 vg\) が働きます。

以上を考慮すれば、次式に示すつり合いの式が成立することが分かります。

\[ \Pi(h)S - \Pi(h + dh)S - N(h) mg + N(h) \rho_0 vg = 0 \]

\(\Pi(h + dh)\) をテイラー1次近似すれば

\[ \Pi(h + dh) \simeq \Pi(h) + \left( \frac{\partial \Pi}{\partial h} \right)_T dh \]

と書けるので、式(3)に戻して整理していくと

\[ \begin{align*} &\text{eq(5.1) :} ~~~~~ \Pi(h + dh) - \Pi(h) = - \frac{N(h)}{S} (m - \rho_0 v) g \\[15pt] &\text{eq(5.2) :} ~~~~~ \left(\frac{\partial \Pi}{\partial h}\right)_T dh = - \frac{N(h)}{S} (m - \rho_0 v) g \\[15pt] &\text{eq(5.3) :} ~~~~~ \therefore ~ \left(\frac{\partial \Pi}{\partial h}\right)_T = - \frac{N(h)}{S dh} (m - \rho_0 v) g \end{align*} \]

が得られます。

次に \(N(h)\) について考えていきます。

\(dh\) を限りなく小さく取れば高さ \(h\) から \(h + dh\) の間の微粒子密度はほぼ一定とみなせるので、微小体積 \(Sdh\) における微粒子数 \(N(h)\) はファント・ホッフの式(2)を用いて

\[ \begin{align*} &\text{eq(6.1) :} ~~~~~ \Pi(h) \cdot Sdh = \frac{N(h)}{N_\text{A}} RT \\[15pt] &\text{eq(6.2) :} ~~~~~ \therefore ~ N(h) = \frac{\Pi(h) \cdot Sdh \cdot N_\text{A}}{RT} \end{align*} \]

と求められます。微粒子数 \(N(h)\) をアボガドロ数で割ることで次元を \([\text{mol}]\) にしていることに注意してください。

式(6.2)を式(5.3)に代入して整理すると次式が得られます。

\[ \left(\frac{\partial \Pi}{\partial h}\right)_T = - \frac{N_\text{A} (m - \rho_0 v) g}{RT} \Pi(h) \]

式(7)を任意の高さを区間にとって積分すれば \(\Pi(h)\) を求めることができます。

\[ \begin{align*} &\text{eq(8.1) :} ~~~~~ \frac{d\Pi}{\Pi} = - \frac{N_\text{A} (m - \rho_0 v) g}{RT} dh \\[15pt] &\text{eq(8.2) :} ~~~~~ \int_{\Pi(h_0)}^{\Pi(h)} \frac{d\Pi}{\Pi} = - \int_{h_0}^h \frac{N_\text{A} (m - \rho_0 v) g}{RT} dh \\[15pt] &\text{eq(8.3) :} ~~~~~ \ln \frac{\Pi(h)}{\Pi(h_0)} = - \frac{N_\text{A} (m - \rho_0 v) g}{RT} (h-h_0) \\[15pt] &\text{eq(8.4) :} ~~~~~ \therefore ~ \Pi(h) = \Pi(h_0) \exp \bigg[ - \frac{N_\text{A} (m - \rho_0 v) g}{RT} (h-h_0) \bigg] \end{align*} \]

導いた式(8.4)に改めて式(6)を用いれば、浸透圧を微粒子数で書き換えた次式が得られます。

\[ N(h) = N(h_0) \exp \bigg[ - \frac{N_\text{A} (m - \rho_0 v) g}{RT} (h-h_0) \bigg] \]

式(9)は沈降平衡状態にある微粒子の分布を記述しており、高さ \(h\) が大きくなるにつれて微粒子数 \(N(h)\) は小さくなっていきます。

任意の2点の高さに存在する微粒子の数を細かく測定して式(8)に適用すれば、アボガドロ定数を求めることができます。

ペランによる様々な実験によって求められたアボガドロ定数はそれぞれで良い一致を示すことを確認。

こうして分子の存在が認められる様になり、更に精密な実験によってアボガドロ定数が次のように定められました。

\[ N_\text{A} = 6.022 \times 10^{23} ~ [\text{/mol}] \]