熱力学における重要法則である熱力学第一法則の解説をします。

また熱力学第一法則の導出も考えていきますよ！

熱力学第一法則

熱力学第一法則とは、系の内部エネルギー変化 \(\Delta U\) を「仕事 \(W\)」と「熱 \(Q\)」を用いて表したものであり、次式のように表現されます。

\[ \Delta U = U(T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) - U(T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) = -W + Q \]

要するに、系が外界との間で仕事・熱のやり取りを行うことによって状態A \((T_\text{A}; ~ V_\text{A}, ~ n_\text{A})\) から状態B \((T_\text{B}; ~ V_\text{B}, ~ n_\text{B})\) に変化する状況を表しています。

\[ (T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) ~ \rightarrow ~ (T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) \]

また内部エネルギーについて図のように、等温環境下に置かれた状況を考えた場合、操作前後における系の温度は等しいので

熱力学第一法則は、様々な条件下における系の状態変化を記述できる一般化された関係であり…

例えば、系が断熱されていれば外部環境との熱のやり取りは \(Q = 0\) となるので

\[ \Delta U = -W \]

という関係が導かれます。これは内部エネルギーと断熱仕事の関係に他なりません。

また系が体積変化をせず、つまり外界に仕事をしない場合は \(W = 0\) となるので

\[ \Delta U = Q \]

といったように、系と外部環境との温度差によって生じる内部エネルギー変化の関係が導かれます。

また、関係式(1)の仕事と熱の符号には注意しましょう。

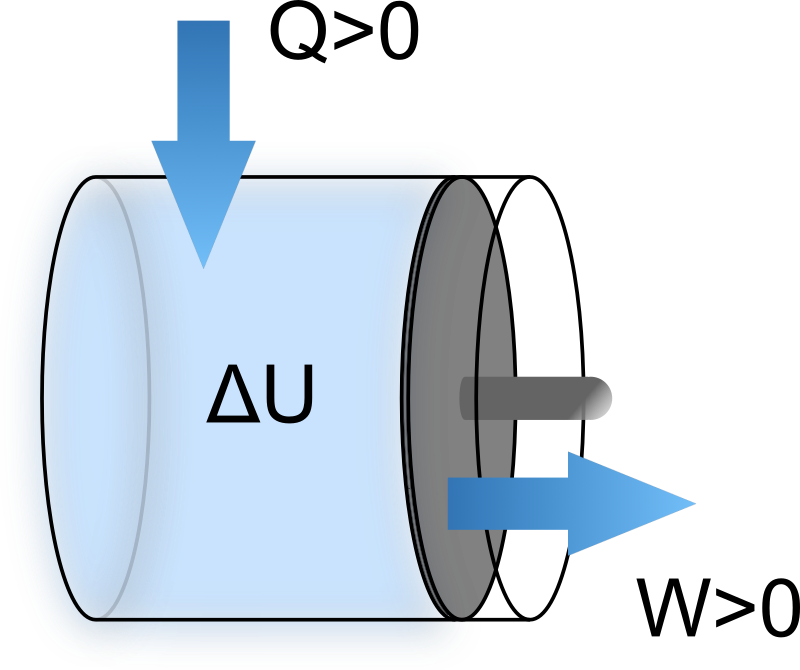
内部エネルギーは系が外界に正の仕事をしたときに減少するように取っています。逆に外部環境から熱が系に流れたときに内部エネルギーは増加します。

これは、次の様な「エネルギー収支の式」と同じ表式になっていて、次図のようにエネルギーが入ったり出ていったりする様子を想像すると分かりやすいです。

熱力学第一法則の導出

熱力学第一法則の導出を行って、式(1)が正しいことを確認してみましょう。

次のような、着目したいピストン付きの容器の周囲を更に断熱容器で覆った複合系を考えます。

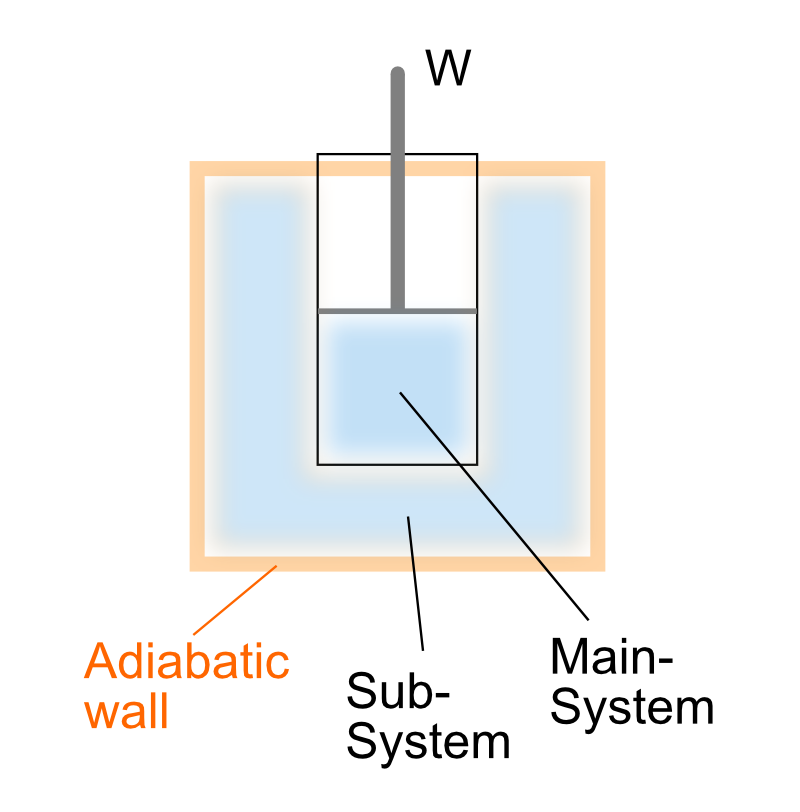
中央の容器は断熱されていないので外側の容器との間で熱のやり取りができます。

また中央の容器の体積が変化するとき断熱壁よりも外側へ仕事をするように設計しています。つまり外側の容器は体積変化しないということです。

この複合系が外界へ仕事をしたとき、エネルギー収支がどの様になるのか考えていきます。

複合系が状態変化するとき、中央の容器の状態変化と外側の容器の状態変化を同時に考える必要があります。

それぞれの容器の体積を \(\boldsymbol{V} = (V, ~ V_\text{sub})\) という組として、また物質量を \(\boldsymbol{n} = (n, ~ n_\text{sub})\) という組として扱うことにすると、複合系がある状態Aから状態Bに変化する様子は次のように表現できます。

\[ (T_\text{A}; ~ \boldsymbol{V}_\text{A}, ~ \boldsymbol{n}) ~ \xrightarrow{\text{a}} ~ (T_\text{B}; ~ \boldsymbol{V}_\text{B}, ~ \boldsymbol{n}) \]

具体的に表現すると

\[ (T_\text{A}; ~ (V_\text{A}, ~ V_\text{sub}), (n_\text{A}, ~ n_\text{sub})) ~ \xrightarrow{\text{a}} ~ (T_\text{B}; ~ (V_\text{B}, ~ V_\text{sub}), (n_\text{B}, ~ n_\text{sub})) \]

と言った具合です。

少し煩雑なので、中央の容器と外側の容器について変化前後の状態を表にまとめておきます。

	操作前	操作後
中央の容器	\((T_\text{A}; ~ V_\text{A}, ~ n_\text{A})\)	\((T_\text{B}; ~ V_\text{B}, ~ n_\text{B})\)
外側の容器	\((T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub})\)	\((T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub})\)

続いて、断熱操作(2)について成立する関係を考えます。

複合系の内部エネルギー変化は、外界への仕事 \(W\) だけなので次式が成立します。

\[ U(T_\text{A}; ~ \boldsymbol{V}_\text{A}, ~ \boldsymbol{n}) = U(T_\text{B}; ~ \boldsymbol{V}_\text{B}, ~ \boldsymbol{n}) + W \]

ここで注意しなければならないのは、式(4)の仕事 \(W\) が断熱仕事 \(W_\text{ad}\) ではないことです。

断熱仕事とは、断熱系"全体"が外界にする仕事のことであり、今考えている複合系は中央の容器しか仕事することができません。そのため \(W\) は断熱仕事とは一致しないのです。

また内部エネルギーの相加性から、複合系の内部エネルギーは中央の容器と外側の容器の内部エネルギーの和に分解できます。

\[ \begin{align*} U(T_\text{A}; ~ \boldsymbol{V}_\text{A}, ~ \boldsymbol{n}) = U(T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) + U(T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub}) \\[15pt] U(T_\text{B}; ~ \boldsymbol{V}_\text{B}, ~ \boldsymbol{n}) = U(T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) + U(T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub}) \end{align*} \]

つまり式(4)は次のように書き換わります。

\[ \begin{align*} & U(T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) + U(T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub}) \\[15pt] & = U(T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) + U(T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub}) + W \end{align*} \]

ここで外側の容器における状態変化のみに着目します。

\[ (T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub}) ~ \rightarrow ~ (T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub}) \]

外側の容器は体積が一定であり温度しか変化しないので、内部エネルギー変化は熱移動で説明できますね。

\[ U(T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub}) - U(T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub}) = Q_\text{sub} \]

ここで \(Q_\text{sub}\) は中央の容器から外側の容器に流入した熱を表しています。

そして式(6)を式(5)に代入すれば次式を得ることができます。

\[ U(T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) - U(T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) = - W - Q_\text{sub} \]

最後に中央の容器の吸熱量 \(Q\) と外側の容器の吸熱量 \(Q_\text{sub}\) は保存関係 \(Q + Q_\text{sub} = 0\) が成立することを利用すれば、熱力学第一法則 ( 式(1) ) を得ることができます。

\[ U(T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) - U(T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) = - W + Q \]

また外側の容器は体積を無限に取ることによって等温環境とみなすことができます。

考えてみても納得できるかと思われますが、非常に大きい容器の一箇所で何らかの変化が起きたとしても全体に及ぼされる影響はほぼ無視できます。

例を上げるなら湯船に少量の水滴を垂らすようなもので、実際湯船はほとんど温度変化しないでしょう。

以上の現象を数学的に示すには \(V_\text{sub} \rightarrow \infty\) かつ \(n_\text{sub} \rightarrow \infty\) という極限を考えればよいのですが…当サイトでは説明は割愛します。

詳細は『熱力学 現代的な視点から （新物理学シリーズ）田崎晴明 著』を参照下さい。本書には小難しい説明がなされているように思いますが、高校過程で学習する不定形 \(0 \times \infty\) の理解があれば簡単に読み解くことができます。

広告

上記の計算を進めると分かりますが \(T_\text{B} \rightarrow T_\text{A}\) という必要条件が課されるので、\(T_\text{A} = T_\text{B} ~ ( ~ \equiv T ~ )\) を式(1)に適用することによって等温条件で成立する熱力学第一法則を得ることができます。

\[ U(\textcolor{red}{T}; ~ V_\text{B}, ~ n_\text{B}) - U(\textcolor{red}{T}; ~ V_\text{A}, ~ n_\text{A}) = - W + Q \]