\[ \text{HCl} ~ \xrightarrow{~~~ \text{H}_2 \text{O} ~~~} ~ \text{Cl}^- + \text{H}^+ \text{ : Arrhenius acid} \\[15pt] \text{NaOH} ~ \xrightarrow{~~~ \text{H}_2 \text{O} ~~~} ~ \text{Na}^+ + \text{OH}^- \text{ : Arrhenius base} \]

\(\text{HCl}\) は塩化水素を表す化学式で気体状態で存在します。この物質は水に溶解すると強い解離性を示し、塩化水素は塩化物イオン \(\text{Cl}^-\) と水素イオン \(\text{H}^+\) に分かれます。

このように水に溶解することで解離し、水素イオンを生じる物質をアレニウス酸と言います。

一方で、\(\text{NaOH}\) は水酸化ナトリウムを表し、常温で白色固体として存在しますが、これを水に溶解させることでナトリウムイオン \(\text{Na}^+\) と水酸化物イオン \(\text{OH}^-\) に解離します。

酸とは異なり、水に溶解することで解離し、水酸化物イオンを生じる物質をアレニウス塩基と言います。

また紹介が遅れてしまいましたが、元の分子からその一部分がイオン状態で解離することを電離と呼びます。

ブレンステッド酸塩基

続いて当コンテンツでのメインであるブレンステッド酸塩基の説明に移ります。

この定義の着想を得るには、アンモニアを例に考えると非常に分かりやすいです。

アンモニアとは化学式 \(\text{NH}_3\) で与えられる物質で塩基性物質として知られています。

ところがアンモニアの組成には水酸化物イオン由来の構造が含まれておらず、これではアレニウスの定義を満たしていません。

そこでブレンステッド塩基の登場です。この問題は次のような化学反応式を考えることによって解決することができます。

式(2)

\[ \text{NH}_3 + \text{H}_2 \text{O} ~ \rightarrow ~ \text{NH}_4^+ + \text{OH}^- \]

このように分子内に水酸化物由来の構造をもっていなくとも間接的に水酸化物イオンを生成するならば塩基性と呼んでも良いのではないでしょうか。

しかし塩基性物質についてだけ特別なルールが増えてしまい、何か不公平感を覚えてしまうのは否めません。ということで酸性物質についても同様に考えてあげましょう。

式(3)

\[ \text{HCl} + \text{H}_2\text{O} ~ \rightarrow ~ \text{Cl}^- + \text{H}_3\text{O}^+ \]

ここで現れた \(\text{H}_3\text{O}^+\) という物質はオキソニウムイオンという名称が与えられています。

実は、アレニウス酸の説明の際に登場した水素イオン \(\text{H}^+\) ですが、こちらは単体で存在するのでは無く、本来オキソニウムイオンとして存在するものなのです。もちろんそれは水中における話であるため、状況に応じて判断する必要があります。

さて、ブレンステッド酸塩基の反応を明らかにしましたが、これらの反応からより抽象化された事実を抜き出していきます。

すなわちそれがブレンステッド酸塩基の定義となります。

アレニウスの定義では、酸および塩基を特徴づけるのはそれぞれ水素イオン、水酸化物イオンを放出するものでしたが、このブレンステッド酸塩基では水素イオンのみで次のように説明することができるでしょう。

酸性物質は水素イオンを自信以外の別の分子へ差し出す物質であり、逆に塩基性物質は水素イオンを自信以外の別の分子から受け取る物質であるということです。

専門用語では、水素イオンのことをプロトンと呼び、また何らかの化学種を差し出す物質のことを供与体、逆に受け取る物質のことを一般に受容体と表現します。

つまり、ブレンステッドの定義によると塩基はプロトン受容体であり、酸はプロトン供与体という表現となり、その様に呼ぶことも恐らくあるので覚えておいて下さい。

以上でブレンステッドの定義によりアレニウスの定義で説明できなかった問題を見事に回避することができるようになったことが理解できたかと思われます。

酸と塩基は相対的に決定される

またブレンステッドの定義を採用することによって少し不思議なことが起こります。

例えば反応式(2)において、アンモニアは前述の通り塩基であり、これは周囲の水分子から水素イオンを受け取ろうとします。

逆に水分子の立場になって考えてみると、水分子はアンモニア分子に水素イオンを供与したことになり、ブレンステッドの定義に従えば「酸」として振る舞っていることになります。

一方で反応式(3)の場合ではどうでしょうか。塩化水素は水に溶解すると電離して水素イオン放出します。そしてその水素イオンを受け取るのは周囲の水分子です。

つまりこのとき水はブレンステッドの定義によると「塩基」として働いていることが分かるでしょうか。

「いや水は中性物質だ」と言ってブレンステッドの定義は間違いであると決めつけるのは早計です。

そもそも中性物質というのは私達の感覚的なところが含まれているとは思わないでしょうか。例えば、触っても平気であるなど。

酸性物質のトップと塩基性物質のトップといった絶対的なものがそれぞれ存在するかのような、そして水はそれらのちょうど中間に位置するため中性物質なのだ、と考えるのがアレニウスの定義と言えるでしょう。

そうではなく、酸性や塩基性とは相対的なものであると考えなくてはならないのです。

なぜなら、酸であるか塩基であるかは反応に関わる2つの分子についてどちらが水素イオンを放出しやすいか、どちらが水素イオンと親和しやすいかで決まるからです。

この考えはこれまでの固定観念を180度回転させます。

例えば普通一般に塩基と言われるアンモニアが入った容器内に別の"超"強い塩基 ( \(\text{B}\) ) を添加する、とアンモニアから水素が引き抜かれ、結果としてアンモニアイオン \(\text{NH}_2^-\) が生成することもあり得るということです。

式(4)

\[ \text{NH}_3 + \text{B} ~ \rightarrow ~ \text{NH}_2^- + \text{HB}^+ \]

※この例はアンモニア水に強い塩基を加えるのではなく、液体アンモニアに強い塩基を加えなければ実現はできないことに注意。詳細は水平化効果を説明する際に触れます。

ブレンステッドの定義からこのときアンモニアは「酸」として振る舞っていることになります。

このように酸性物質および塩基性物質が絶対的なものではなく、反応する2分子間における酸塩基強度の比較で決まることを押さえておきましょう。

酸塩基平衡

前節で酸と塩基の強度について触れましたが、一体何がどうなると強い酸や弱い酸などと言うことができるのでしょうか。

酸塩基平衡と電離度

酸・塩基の強度を理解するに当たって、前提となる知識があります。

それは、酸塩基反応とは平衡反応であるということです。

つまり前節で示してきた反応式は実は一方向の矢印ではなく、双方向に向いた矢印で表現しなければならなかったのです。

例えば酸を水に溶解したときの反応式は、酸を一般に \(\text{HA}\) と表現することにして次のように記述されることになります。

式(5)

\[ \text{HA} + \text{H}_2\text{O} ~ \rightleftharpoons ~ \text{A}^- + \text{H}_3\text{O}^+ \]

平衡反応であるということは、左辺と右辺の物質がそれぞれある割合で存在することを表しているのですが、これはすなわち全ての\(\text{HA}\) 分子が水素イオンを放出してイオン \(\text{A}^-\) として存在するわけではないことを言っています。

どの程度分子から水素イオンが電離しているかを定量的に表す方法として、電離度が用いられます。記号を \(\alpha\) とすると、数学的に次式で表現できます。

式(6)

\[ \alpha = \frac{[\text{A}^-]}{[\text{HA}] + [\text{A}^-]} \]

一方で塩基 \(\text{B}\) を水に溶解させた場合では、反応式は次のとおりとなります。

式(7)

\[ \text{B} + \text{H}_2\text{O} ~ \rightleftharpoons ~ \text{HB}^+ + \text{OH}^- \]

反応式(7)についても電離度を定義できて、区別するために \(\beta\) と表せば次式のようになります。

式(8)

\[ \beta = \frac{[\text{HB}^+]}{[\text{B}] + [\text{HB}^+]} \]

そして、電離度は酸や塩基の強さを表す1つ指標となっていて、電離度が大きいほど酸あるいは塩基としての強度が強いと言うことができるのです。

共役酸と共役塩基

また酸塩基反応が平衡反応であるために、次のことも言えるようになります。

はじめ \(\text{HA}\) であった酸は水素イオンを水に供与することによって\(\text{A}^-\) となりますが、逆に \(\text{A}^-\) はオキソニウムイオンの水素を受容することによって \(\text{HA}\) に戻ることができるため、その際は塩基として働くことになります。

また水は塩基として振る舞うことによって \(\text{HA}\) から水素イオンを受け取りオキソニウムイオンとなりますが、オキソニウムイオンの状態からは \(\text{A}^-\) に水素イオンを供与する事ができるために酸として役割を果たします。

つまりまとめると、「酸」は塩基と反応すると「塩基」となり、逆に「塩基」は酸と反応すると「酸」になる、ということです。

反応式にしてみると次のように書くことができます。

式(9)

\[ \text{Acid}_1 + \text{Base}_2 ~ \rightleftharpoons ~ \text{Base}_1 + \text{Acid}_2 \]

反応前後の物質の対応は同じ添字にて表現しました。

このとき、\(\text{Base}_1\) は \(\text{Acid}_1\) の共役塩基、また \(\text{Acid}_2\) は \(\text{Base}_2\) の共役酸と言います。

例えば反応式(5)で言えば、\(\text{A}^-\) が \(\text{HA}\) の共役塩基、オキソニウムイオンは水の共役酸となります。

酸と塩基の強度

酸解離定数・塩基解離定数

ここまでで説明した酸塩基平衡反応を基にして、本題である酸・塩基の強度の定量化を進めていきましょう。

といったものの、分子がどの程度解離しているのかを表す「電離度」を用いれば各々の物質の強度として定めることができるのではないか? これ以上何らかの数値を求める必要など無いのではないか? とも考えられるのですが、

実は電離度は溶媒に溶解させる物質の濃度によって変化するため、物質固有の値として利用するには不便なのです。

実際にどのように変化するかについては次の項で明らかになります。

まずは電離度よりも適した量を選択する必要性があるということを認識していただければ結構です。

では一体どのようにして酸・塩基の強度を決定するかと言うと、酸塩基反応が平衡反応であるということから平衡定数を利用すれば良いのです。

平衡定数は温度が一定であれば常に一定値をとることを思い出してください。

さっそく反応式(5)の状態について考えると、平衡定数 \(K\) は次式で与えることができます。

式(10)

\[ K = \frac{\text{[A}^-\text{]}\text{[H}_3\text{O}^+\text]}{[\text{HA}]} \]

さて多くの方がここで疑問を抱かれるのですが、反応に水が関与しているために次の表式が正しいのではないか? と言うのです。

式(11)

\[ K = \frac{\text{[A}^-\text{]}\text{[H}_3\text{O}^+\text]}{[\text{HA}][\text{H}_2\text{O}]} ~ (?) \]

しかし式(11)は全くの誤りだと断言しておきましょう。

というのも、よくある説明として、

水は溶媒であり多量にあるため、化学反応による濃度変化はほとんど認められない。

したがって、\([\text{H}_2\text{O}]\) は近似的に一定とみなせるために式(11)に両辺 \([\text{H}_2\text{O}]\) を掛けて

\[K [\text{H}_2\text{O}] = \frac{\text{[A}^-\text{]}\text{[H}_3\text{O}^+\text]}{[\text{HA}]}\]

とした後、\(K [\text{H}_2\text{O}]\) を新たな平衡定数として定める。

などと解説がなされますが、最後に水の濃度を平衡定数に吸収させるというのは全く誤った解釈なのです。

一歩譲って、水が溶媒であるために濃度変化がほとんど認められないということは（溶質が希薄な条件下においては）正しいでしょう。

その結果として近似的に \([\text{H}_2\text{O}]\) の項がキャンセルされるというのが熱力学的な説明になるのですが…

ただ残念ながら当コンテンツではそこまで踏み込むことができないので、詳細は別のコンテンツに譲ることにさせて下さい。

※熱力学のコンテンツは作成準備中です。

一般的に式(10)で表現される平衡定数は酸解離定数と呼ばれ、\(K_a\) の記号が用いられます。改めて提示しておくことにしましょう。

式(12)

\[ K_a = \frac{\text{[A}^-\text{]}\text{[H}_3\text{O}^+\text]}{[\text{HA}]} \]

また、塩基性物質についても同様の議論により塩基解離定数 \(K_b\) を定めることができます。

式(13)

\[ K_b = \frac{[\text{HB}^+][\text{OH}^-]}{[\text{B}]} \]

\(K_a\) の計算方法

次に実際に酸解離定数を求める方法を示しましょう。

以下に示すように、反応式に基づいて

反応開始前の始状態 ( Initial state )
反応による濃度変化
最終的に平衡に落ち着いたときの状態 ( Final state )

を考えると非常に分かりやすいです。

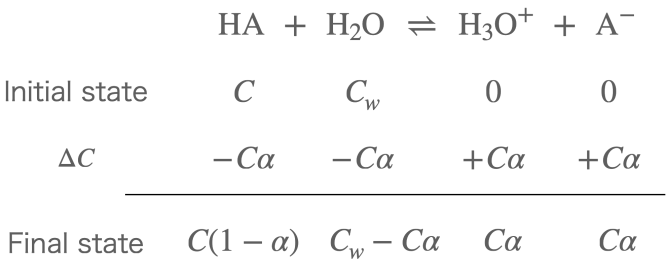
\(C\) は酸 \(\text{HA}\) の初期濃度であり、これは私達の調製次第で操作することが可能です。

\(C_w\) は水の濃度であり、\(C\) と比較すると普通何百、何千倍ほど大きさが異なります。

\(\alpha\) は電離度を表しています。

それではこの計算式の説明をしましょう。

Initial state の行、すなわち初期状態では酸 \(\text{HA}\) および水の濃度はそれぞれ \(C\), \(C_w\) です。酸を水に溶解した瞬間を指しますので、このときはまだ生成物の濃度は0となっています。

続いて \(\Delta C\) の行、これは化学反応によるそれぞれの物質の濃度変化を表しています。酸が電離度 \(\alpha\) 分だけ解離したとすると \(C\alpha\) で表現できます。一方生成物は \(C\alpha\) だけ増加することになります。

最後に Final state の行で平衡状態に達したときですが、こちらは上記2つの状態で求めた量を縦向きに足していけば求めることができます。

以上まとめると、平衡状態に置いて各物質の濃度は以下のようになります。

式(14)

\[ [\text{HA}] = C(1 - \alpha) \\[15pt] [\text{H}_3\text{O}^+] = C\alpha \\[15pt] [\text{A}^-] = C\alpha \]

ここで実験的に水素イオン濃度を測定します。すると、酸 \(\text{HA}\) の初期濃度 \(C\) は既知であるため、2つ目の式を利用することによって電離度 \(\alpha\) を数値として得ることができます。

そして式(14)を式(12)に代入すれば、\(K_a\) を \(C\) および \(\alpha\) のみで表現できて、

式(15)

\[ K_a = \frac{C\alpha^2}{1 - \alpha} \]

結果として酸 \(\text{HA}\) の \(K_a\) が数値として得られることになります。

ちなみにこれをオストワルドの希釈律と呼んだりします。

また前項で触れた「電離度と濃度の関係」が明らかとなっています。\(K_a\) が一定値をとるため、\(C\) の変化に従属して \(\alpha\) が変化することが伺えるでしょう。

さらに同式は塩基性物質にも成立して、つまり \(K_a\) を \(K_b\) に、また \(\alpha\) を \(\beta\) に置き換えたものが先程と同様の手続きで得ることができます。

式(16)

\[ K_b = \frac{C\beta^2}{1 - \beta} \]

続いて具体的な例として酢酸の酸解離定数を示しましょう。

酢酸の酸解離定数

\[ K_a = 1.75 \times 10^{-5} \]

この例のように一般に \(K_a\) は非常に小さな値を取ります。

この定数から概算してみても、仮に系に100万個の酢酸分子が存在する場合、酢酸イオンとして解離した分子は4分子程度しか存在しないことになります。

そのため通常、常用対数をとって扱いやすくすることもあります。

式(17)

\[ \text{p}K_a \equiv - \log K_a \]

これは塩基解離定数に関しても同様に \(\text{p}K_b \equiv - \log K_b\) で表現されます。

実際に式(17)を利用すれば先程の酢酸の例では \(\text{p}K_a = 4.76\) という値になって、\(K_a\) で表現するよりも整頓されます。

ただし定義にもある通り、負号が付いているために扱いには注意が必要です。

対数を取る前の \(K_a\) では値が大きいほど酸としての強度が強いことを表していましたが、\(\text{p}K_a\) の場合は値が小さいほど強い酸であることを示します。

また \(\text{p}K_b\) の場合も同様、小さい値を示すほど強い塩基として振る舞います。

\(\text{p}K_a\) を利用した反応予測

\(\text{p}K_a\) の優れたところは、強度を定量化することだけではありません。

前述した通り、酸と塩基はそれぞれ相対的に決定されます。

そのため、2つの物質の \(\text{p}K_a\) を比較することによって、どちらが水素イオンを放出しやすいのかを予測することができるようになります。

ただし、2つの反応物の間で \(\text{p}K_a\) を比較するのではありません。

なぜなら酸塩基反応は常に酸と塩基がセットとなって反応するため、反応物について \(\text{p}K_a\) を考えるとしても必然的に一方の物質のみにしか当てはめることができないからです。

では比較を行うための2つ目の \(\text{p}K_a\) はどこから用意すればいいかというと、以下に再掲しますが反応式(9)を思い出していただければ生成物側に共役酸があることに気がつくでしょう。

式(9)

\[ \text{Acid}_1 + \text{Base}_2 ~ \rightleftharpoons ~ \text{Base}_1 + \text{Acid}_2 \]

この反応式を酸 \(\text{HA}\) および塩基 \(\text{B}\) を利用して書き換えれば次のようになります。

式(18)

\[ \text{HA} + \text{B} ~ \rightleftharpoons ~ \text{A}^- + \text{HB}^+ \]

ここで現れる共役酸 \(\text{HB}^+\) の酸解離定数を上手く利用することで反応式(18)の反応がどちらに進みやすいのか予測を行うことができるようになるのです。

共役酸の酸解離定数 \(\text{p}K_{\text{HB}^+}\)

まだ共役酸の酸解離定数を定式化していませんでしたので、ここで行うことにしましょう。

その手続きは式(12)で \(K_a\) を定めたときと差ほど変わりありません。

次の化学反応式を考えます。

式(19)

\[ \text{HB}^+ + \text{H}_2\text{O} ~ \rightleftharpoons ~ \text{B} + \text{H}_3\text{O}^+ \]

共役酸 \(\text{HB}^+\) の酸解離定数を \(K_{\text{HB}^+}\) と表すことにしましょう。するとそれは次式で与えることができます。

式(20)

\[ K_{\text{HB}^+} = \frac{[\text{B}][\text{H}_3\text{O}^+]}{[\text{HB}^+]} \]

これは前節で求めた \(K_a\) と同様に \(K_{\text{HB}^+}\) の値が大きいほど共役酸 \(\text{HB}\) は多くの水素イオンを放出することになります。

また対数をとって \(\text{p}K_{\text{HB}^+}\) とすれば、小さな値を取るほど酸の強度が強いことを示すことも問題ないでしょう。

解離定数から反応を予測する

さてここで、反応式(18)の平衡定数を考えてみましょう。ただし、\(\text{HA}\) あるいは \(\text{B}\) が水以外の場合であるとします。どちらかを水にすると前節で酸解離定数および塩基解離定数を定めたときの話に戻ってしまいます。

状況としては、水に酸 \(\text{HA}\) および塩基 \(\text{B}\) を少量ずつ溶解させたものと思っていただければ良いでしょう。

このとき平衡定数は次式で与えられます。

式(21)

\[ K = \frac{[\text{A}^-][\text{HB}^+]}{[\text{HA}][\text{B}]} \]

式(21)をよく見てみると、実は \(\text{p}K_a\) および \(\text{p}K_{\text{HB}^+}\) を用いて書き換えるられることに気づきます。

式(22)

\[ K = \frac{K_a}{K_{\text{HB}^+}} \]

このように一般的な酸塩基反応について成立する平衡定数が、系に存在し得る酸および共役酸の酸解離定数だけで表現されます。そしてこれが反応予測に利用できる関係式となるのです。

もし \(K\) が大きければ、すなわち分子にある \(K_a\) が大きければ、反応式(18)の平衡は生成物側に偏ることになります。

言い換えれば、反応物である酸 \(\text{HA}\) は生成物である共役酸 \(\text{HB}^+\) と比較して水素イオンを供与しやすい性質にあるために前者が \(\text{A}^-\) の状態になりやすい、すなわち生成物側に平衡が傾くということです。

逆に、分母にある \(K_{\text{HB}^+}\) が大きいと、\(K\) が小さくなるので、全体としての反応は進みにくいことを表します。

これは生成する共役酸 \(\text{HB}^+\) の方が反応物の酸 \(\text{HA}\) よりも水素イオンを供与しやすい性質であるためです。

また式(22)を対数で表現するとどうなるでしょうか。\(- \log K \equiv \text{p}K\) として計算を進めると次式が得られます。

式(23)

\[ \text{p}K = \text{p}K_a - \text{p}K_{\text{HB}^+} \]

\(K\) が大きく反応が進みやすい系では、\(\text{p}K\) は負の値を取るようになります。

式(24) : 反応が進む系

\[ \begin{align*} \text{p}K &= \text{p}K_a - \text{p}K_{\text{HB}^+} < 0 \\[15pt] \Leftrightarrow ~ & \text{p}K_a < \text{p}K_{\text{HB}^+} \end{align*} \]

つまり平衡が右に傾くには \(\text{p}K_a\) が \(\text{p}K_{\text{HB}^+}\) よりも小さい値である必要があります。

以上のことを理解していただいた上で、式(21)を利用して次の反応がどのように進むのかを予測してみましょう。

\[ \text{CH}_3\text{COOH} + \text{NH}_3 ~ \rightleftharpoons ~ \text{CH}_3\text{COO}^- + \text{NH}_4^+ \]

ただし、酢酸 \(\text{CH}_3\text{COOH}\) およびアンモニウムイオン \(\text{NH}_4^+\) の酸解離定数 \(\text{p}K_a\) はそれぞれ、4.76, 9.24 とします。

するとそれらの値からただちに反応物側の \(\text{p}K_a\) が共役酸のそれよりも小さいため平衡は右に偏ることが分かるのです。