見かけ上 系の状態に変化がないとき平衡状態にあると言い、対して状態に変化があるとき非平衡状態にあると言います。

例えば異なる温度の物体を接触させたとき高温物体から低温物体へ熱移動が生じますが、まさにこれは非平衡状態にある系の一例です。

当ページでは、非平衡状態にある系が内部の温度差・圧力差によってどの様な変化を生じるか理論的に導いていきます。

非平衡状態とエントロピー

熱力学では見かけ上 系の状態に変化がないとき平衡状態にあると言い、対して状態に変化があるとき非平衡状態にあると言います。

例えば次のような操作について

\[ (T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) ~ \rightarrow ~ (T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) \]

平衝状態A \((T_\text{A}; ~ V_\text{A}, ~ n_\text{A})\) から平衝状態B \((T_\text{B}; ~ V_\text{B}, ~ n_\text{B})\) に変化するとき、その途中では一般に非平衡状態となります。

※ただし準静的過程を経由した変化の場合は、操作の最中で常に平衡状態を維持させることは可能です。

また、この操作(1)が自発的に起こる場合、要するに外から力を加えなくとも系が勝手に状態Aから状態Bに向かうとき、エントロピー増大の法則に従って次の関係が成立します。

\[ S(T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) < S(T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) \]

この様に系が非平衡状態をたどって変化するとき、系のエントロピーは必ず増加してしまいます。逆を言えば、エントロピー増大の法則を利用して系に生じる変化を予測できるという事です。

非平衡状態の温度変化

冒頭でも述べたように、異なる温度の物体を接触させると高温物体から低温物体へ熱が移動します。

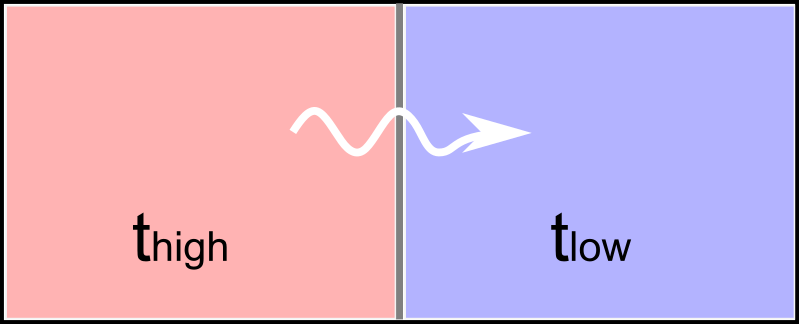
熱移動によって高温だった物体は始めより温度が下がり、低温だった物体は温度が上がります。熱移動による物体の温度変化が生じている最中は、まさに系は非平衡の状態にあり系のエントロピーは増大して行っていると言えます。

実際にエントロピー増大の法則からも、経験的事実と合致する結果が得られることを確認していきたいのですが、前提としてこの法則を利用するためには系が断熱されている必要があります。

そこで高温物体と低温物体を接触させた複合系は、外と熱のやり取りを行わないとしておきましょう。

始め高温物体は \((T_1; ~ V_1, ~ n_1)\)、低温物体は \((T_2; ~ V_2, ~ n_2)\) の状態にあるとします。

各物体を接触させ、終状態でそれぞれ温度が \(\Delta T_1\), \(\Delta T_2\) だけ変化したときについてエントロピー増大の法則を適用すると次のようになります。

\[ S\big( (T_1; ~ V_1, ~ n_1), ~ (T_2; ~ V_2, ~ n_2) \big) < S\big( (T_1 + \Delta T_1; ~ V_1, ~ n_1), ~ (T_2 + \Delta T_2; ~ V_2, ~ n_2) \big) \]

	高温物体	低温物体
始状態	\((T_1; ~ V_1, ~ n_1)\)	\((T_2; ~ V_2, ~ n_2)\)
終状態	\((T_1 + \Delta T_1; ~ V_1, ~ n_1)\)	\((T_2 + \Delta T_2; ~ V_2, ~ n_2)\)

エントロピーの相加性から複合系のエントロピーは、各部分系のエントロピーの和として次のように書き換えることができます。

\[ S_1(T_1; ~ V_1, ~ n_1) + S_2(T_2; ~ V_2, ~ n_2) < S_1(T_1 + \Delta T_1; ~ V_1, ~ n_1) + S_2(T_2 + \Delta T_2z; ~ V_2, ~ n_2) \]

式(3)の右辺について、テイラー1次近似を用いると

\[ \begin{align*} &S_1(T_1 + \Delta T_1; ~ V_1, ~ n_1) \simeq S_1(T_1; ~ V_1, ~ n_1) + \left( \frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial T} \right)_{V, ~ n} \Delta T_1 \\[15pt] &S_2(T_2 + \Delta T_2; ~ V_2, ~ n_2) \simeq S_2(T_2; ~ V_2, ~ n_2) + \left( \frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial T} \right)_{V, ~ n} \Delta T_2 \end{align*} \]

となるので、式(3)に戻して整理すると次式が得られます。

\[ \left( \frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial T} \right)_{V, ~ n} \Delta T_1 + \left( \frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial T} \right)_{V, ~ n} \Delta T_2 > 0 \]

エントロピーの温度に関する偏微分係数は、次のように内部エネルギーを用いて表現することができます。( 詳しくはエントロピーの解説ページを参照。)

\[ \left( \frac{\partial S}{\partial T} \right)_{V, ~ n} = \frac{1}{T} \left( \frac{\partial U}{\partial T} \right)_{V, ~ n} \]

式(6)を式(5)に適用させたものが次の式です。

\[ \frac{1}{T_1} \left( \frac{\partial U_1(T_1; ~ V_1, ~ n_1)}{\partial T} \right)_{V, ~ n} \Delta T_1 + \frac{1}{T_2} \left( \frac{\partial U_2(T_2; ~ V_2, ~ n_2)}{\partial T} \right)_{V, ~ n} \Delta T_2 > 0 \]

更に、物体の体積が一定であるとき、内部エネルギー変化は

\[ \Delta U \simeq \left( \frac{\partial U}{\partial T} \right)_{V, ~ n} \Delta T + \left( \frac{\partial U}{\partial V} \right)_{T, ~ n} \Delta V \\[15pt] \xrightarrow{ ~ \Delta V = 0 ~ } ~ \Delta U \simeq \left( \frac{\partial U}{\partial T} \right)_{V, ~ n} \Delta T \]

と表すことができるので、式(7)に適用すると次のようになります。

\[ \frac{1}{T_1} \Delta U_1(T_1; ~ V_1, ~ n_1) + \frac{1}{T_2} \Delta U_2(T_2; ~ V_2, ~ n_2) > 0 \]

いま複合系は外界との間で断熱されているために、系内の内部エネルギー変化の総量は 0 になります。したがって

\[ \Delta U_1(T_1; ~ V_1, ~ n_1) + \Delta U_2(T_2; ~ V_2, ~ n_2) = 0 \]

が成立しているので、式(9)と合わせると結果 次の関係式が得られます。

\[ \begin{gather*} \text{eq(11.1)} ~~~~~ \left( \frac{1}{T_1} - \frac{1}{T_2} \right) \Delta U_1(T_1; ~ V_1, ~ n_1) > 0 \\[20pt] \text{eq(11.2)} ~~~~~ \Leftrightarrow ~ \frac{T_2 - T_1}{T_1 T_2} \Delta U_1(T_1; ~ V_1, ~ n_1) > 0 \end{gather*} \]

さて、式(11)を用いると高温物体1と低温物体2を接触させたときにどの様な変化を生じるかを導くことができます。

それぞれの物体の温度は \(T_1 > T_2\) であるから、直ちに \(\Delta U_1(T_1; ~ V_1, ~ n_1) < 0\) であることが分かります。

そして内部エネルギーは定積熱容量を用いて \(\Delta U = C \Delta T\) で与えられる事から高温物体1の温度変化は \(\Delta T_1 < 0\) となり、低温物体2との接触により温度が下がると言えます。他方 低温物体2では \(\Delta T_2 > 0\) となって高温物体1との接触により温度が上がることも分かるでしょう。

非平衡状態の圧力差による体積変化

熱力学系は圧力差がある場合も非平衡状態となり得ます。

例えば動かせる仕切りで2部屋に分けられた次のような容器を考えましょう。

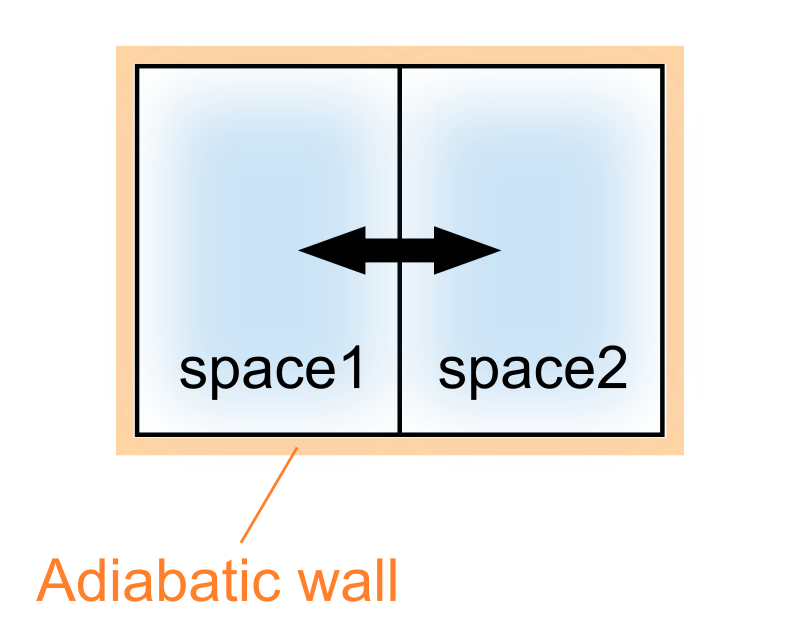
始め仕切りをある位置で固定しておき、部屋1および2の圧力が \(P_1 > P_2\) となるようにしておきます。

仕切りの固定を解いたとき、仕切りは部屋1の体積が増加する方向に動き出すことを力学的にも経験的にも理解していることでしょう。ではエントロピー増大の法則ではどうか？

各部屋の始状態が \((T_1; ~ V_1, ~ n_1)\)、\((T_2; ~ V_2, ~ n_2)\)、
一方、終状態が \((T_1; ~ V_1 + \Delta V_1, ~ n_1)\)、\((T_2; ~ V_2, + \Delta V_2 ~ n_2)\) であるとき、エントロピー増大の法則を適用すると次のようになります。

\[ S\big( (T_1; ~ V_1, ~ n_1), ~ (T_2; ~ V_2, ~ n_2) \big) < S\big( (T_1; ~ V_1 + \Delta V_1, ~ n_1), ~ (T_2; ~ V_2 + \Delta V_2, ~ n_2) \big) \]

	部屋1	部屋2
始状態	\((T_1; ~ V_1, ~ n_1)\)	\((T_2; ~ V_2, ~ n_2)\)
終状態	\((T_1; ~ V_1 + \Delta V_1, ~ n_1)\)	\((T_2; ~ V_2 + \Delta V_2, ~ n_2)\)

※ここで仕切りは透熱性があるとして、平衡状態における各部屋の温度は \(T_1 = T_2\) を満たすことに注意です。詳しくは熱力学的つり合いの解説ページを参照。

エントロピーの相加性から、複合系のエントロピーは各部屋のエントロピーの和に等しいので、式(12)は次式のように書き換えることができます。

\[ S_1(T_1; ~ V_1, ~ n_1) + S_2(T_2; ~ V_2, ~ n_2) < S_1(T_1; ~ V_1 + \Delta V_1, ~ n_1) + S_2(T_2; ~ V_2 + \Delta V_2, ~ n_2) \]

式(13)右辺の項について、テイラー1次近似で展開すると

\[ \begin{align*} &S_1(T_1; ~ V_1 + \Delta V_1, ~ n_1) \simeq S_1(T_1; ~ V_1, ~ n_1) + \left( \frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial V} \right)_{T, ~ n} \Delta V_1 \\[15pt] &S_2(T_2; ~ V_2 + \Delta V_2, ~ n_2) \simeq S_2(T_2; ~ V_2, ~ n_2) + \left( \frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial V} \right)_{T, ~ n} \Delta V_2 \end{align*} \]

となるので、結果 式(13)は次のように整理されます。

\[ \left( \frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial V} \right)_{T, ~ n} \Delta V_1 + \left( \frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial V} \right)_{T, ~ n} \Delta V_2 > 0 \]

ここでエントロピーの体積に関する偏微分係数が、内部エネルギーや圧力と次式の関係にあることを利用します。( 詳しくはエントロピーの解説ページを参照。)

\[ \left( \frac{\partial S}{\partial V} \right)_{T, ~ n} = \frac{1}{T} \left\{ \left( \frac{\partial U}{\partial V} \right)_{T, ~ n} + P \right\} \]

すると式(15)は

\[ \frac{1}{T_1} \left\{ \left( \frac{\partial U_1(T_1; ~ V_1, ~ n_1)}{\partial V} \right)_{T, ~ n} + P_1(T_1; ~ V_1, ~ n_1) \right\} \Delta V_1 + \frac{1}{T_2} \left\{ \left( \frac{\partial U_2(T_2; ~ V_2, ~ n_2)}{\partial V} \right)_{T, ~ n} + P_2(T_2; ~ V_2, ~ n_2) \right\} \Delta V_2 > 0 \]

更に両辺 \(T_1 ( ~ = T_2 ~ )\) をかけて整理すると次のようになります。

\[ \left( \frac{\partial U_1(T_1; ~ V_1, ~ n_1)}{\partial V} \right)_{T, ~ n} \Delta V_1 + P_1(T_1; ~ V_1, ~ n_1) \Delta V_1 + \left( \frac{\partial U_2(T_2; ~ V_2, ~ n_2)}{\partial V} \right)_{T, ~ n} \Delta V_2 + P_2(T_2; ~ V_2, ~ n_2) \Delta V_2 > 0 \]

いま系の状態が変化する前後で温度変化がないため、内部エネルギー変化は体積変化と次の関係が成立します。

\[ \Delta U \simeq \left( \frac{\partial U}{\partial V} \right)_{T, ~ n} \Delta V \]

したがって式(18)は次のように書き換えることができます。

\[ \Delta U_1(T_1; ~ V_1, ~ n_1) + P_1(T_1; ~ V_1, ~ n_1) \Delta V_1 + \Delta U_2(T_2; ~ V_2, ~ n_2) + P_2(T_2; ~ V_2, ~ n_2) \Delta V_2 > 0 \]

式(10)にも示す通り、断熱条件では系が外界に仕事をしない限り
内部エネルギー変化は 0
すなわち \(\Delta U_1 + \Delta U_2 = 0\) となるので、式(20)は更に次のように書き換えられます。

\[ P_1(T_1; ~ V_1, ~ n_1) \Delta V_1 + P_2(T_2; ~ V_2, ~ n_2) \Delta V_2 > 0 \]

各部屋の体積変化の和は 0 であるから

\[ \Delta V_1 + \Delta V_2 = 0 \]

式(21)および式(22)から \(\Delta V_2\) を消去すると、次の関係が導かれます。

\[ \big\{ P_1(T_1; ~ V_1, ~ n_1) - P_2(T_2; ~ V_2, ~ n_2) \big\} \Delta V_1 > 0 \]

始め \(P_1 > P_2\) となるように設定しているので、\(\Delta V_1 > 0\) となって部屋1の体積は増大することが分かります。逆に部屋2の体積は減少します。

このようにエントロピー増大の法則によっても、力学的・経験的に理解できる挙動を説明できます。