様々な事象（現象）を数学的に記述するには、多くの場合「関数」が利用されます。

関数には対象としている事象のあらゆる情報が含まれており、それらを抽出したり上手く利用するためには解析を行う必要があります。

そこで当コンテンツでは最も多用する解析手法として「微分法」を取り上げ、その概念の理解を目的としました。

関数を特徴づけるもの

関数を解析する手段を具体的に見ていく前に、そもそも関数とは何によって特徴付けられるのかを理解しておく必要があるでしょう。

先に言ってしまえば、ある関数 \(y = f(x)\) についてその関数を特徴付けるのは変数 \(x\) の変化に伴なう \(y\) の値の変化です。

ある値 \(x = a\) より少しだけ大きい（あるいは小さい）値を関数に代入したときに、\(y\) の値は大きくなるのか、小さくなるのかを知ることによって関数がどういった挙動を示すのかを知ることができるからです。

例えば、\(y = -x\) という関数では \(x = a\) より大きい値を代入すると \(y\) の値は小さくなっていきます。

以上の内容を以降では数量的に扱っていく必要があるため、次の項で \(x\) の値の変化に伴う \(y\) の値の変化を与える「関数の変化率」の導入を行っていきましょう。

関数の変化率（関数の傾き）

関数の変化率とは前項で少し触れた通り、\(x\) の値の変化に伴う \(y\) の値の変化を表します。

変化を記述するためには、変化前と変化後の2つの状態を予め定める必要があります。

そこで、ある関数 \(y = f(x)\) について定義域に含まれる2点 \(x = a\), \(b\) \((a < b)\) を考えることにしましょう。

このとき \(a\), \(b\) それぞれを関数 \(f(x)\) に代入した結果として得られる \(y\) の値は、\(f(a)\) および \(f(b)\) と表現されます。

さて、それではまず \(x\) の変化を数学的に記述してみます。\(x\) の値を \(a\) から \(b\) に変化させるとき、その変化分は「変化後から変化前を引く」ことによって表すことができます。

\[ b - a \]

一方で \(y\) の値の変化についても同様に変化の前後の差で記述します。

\[ f(b) - f(a) \]

以上2つを次に示すように1つの量にまとめて見ましょう。

式(1)

\[ \frac{f(b) - f(a)}{b - a} \]

式(1)こそが関数の変化率であり、意味合いからしても分母には \(x\) の変化が、それに対して分子には \(y\) の変化を置くことによって目的は達成できたことになります。

また式(1)は、\(xy\) 平面上に2点 A\((a, ~ f(a))\)、B\((b, ~ f(b))\) を取ったとき、それらを通る直線の傾きを表現します。

実際この直線を \(x\) と \(y\) を用いて表すと、式(1)の変化率がそのまま式中に現れることが分かります。

\[ y = \frac{f(b) - f(a)}{b - a} (x - a) + f(a) \]

このように、「変数 \(x\) の変化によってグラフがどのように増加あるいは減少するか」は「関数の変化率」を利用すれば記述できることが理解できました。

以降、一般に式(1)は「変化率」ではなく「傾き」と表現されることが多いので当サイトも例に倣うことにします。

微分法

前節では式(1)を利用することによって、関数が増加するのか或いは減少するのかを数値的に取り扱うことができるようになることを示しました。

しかしながら、関数上の2点を選択してそれらを通る直線について式(1)を適用しようとすると問題が発生します。

例えば、次に示すようなグラフが曲線となる関数の場合です。

グラフ上に2点AおよびBをとり、それらを通る直線を引いています。ここで点Bは点Aから近い点、点B'は点Aから遠い点であることを表しています。

見てのとおり式(1)では曲線の傾きを決定することはできないことが分かるでしょう。

点AとB'を通る直線について傾きを計算してもグラフの傾きとはあまりにも期待外れな結果が得られることは間違いありません。

実際、曲線のグラフは点AからB'にかけて増加→減少をたどっている（つまり上に凸）のにも関わらず、2点を通る直線は常に増加しています。

では一体グラフが曲線となる関数の場合、その傾きはどう定義すれば良いか、という問題が生じます。

この問題を解くためのヒントは先程の図中にあり、式(1)を適用するためのグラフ上の2点を近く選択した場合であれば、正確ではないにしても曲線の傾きをおおよその値として得られる事が期待できそうではないでしょうか。

以下でこの考えをより厳密なものにし、正確な傾きの値が得られないか検討していくことにしましょう。

\(\Delta\) の導入

前項では式(1)を適用するための2点それぞれを近くに取ることで、おおよその曲線の傾きを得る方法を示しました。

以降ではこの2点間の幅が重要な量となってくるので、新たな記号を導入することにします。

式(2)

\[ \Delta x \equiv b - a \]

式(2)は各点A,Bの \(x\) 座標の幅を表していて、更にこれは前節でも示した \(x\) の変化量とも等しいものです。

また \(\Delta\) は文字ではなく記号であることにも注意しましょう。

通常何か別の文字変数とセットになって1つのものとして扱われます（記号ではなく文字として何らかの物理量を意味することもあります）。

次の図は \(\Delta\) の意味を視覚化したものです。

\(x = c\) と言うのは \(x\) 軸上のある点を意味することは問題ないでしょう。

一方、今考えている \(\Delta x\) というのは、\(x\) 軸上のある二点 \(x = a\) と \(x = b\) で挟まれた区間や幅を表現します。

※当サイトの目的である”自然科学”（特に物質科学）においては「幅をもたない点としての量」よりも「幅をもった量」の方がよく扱われます。例えば物体には幅があります。逆に何らかの事象（現象）を理想化する際には、幅を無視したりすることもあります。例えば"質点の力学"などは、質点という幅を持たない点の運動を記述します。

傾きの極限

曲線のグラフの傾きを求める際、式(1)を利用するために設定する2点の幅を近くに取ればおおよその傾きが得られることを期待できます。

つまりこれは前項で導入した \(\Delta x\) を限りなく0に近づけることに相当します。

その結果として、それら2点を通る直線の傾きがどのように変化していくでしょうか。実際に数学的操作を行って見ていきましょう。

まずは前処理として、傾きの式(1)に2点間の幅の式(2)を直接代入して \(\Delta x\) で表現される形式にしておきます。

式(3)

\[ \frac{f(a + \Delta x) - f(a)}{\Delta x} \]

それでは \(\Delta x\) を小さくしていきますが、そのためには次に示す数学的表現を用いて記述することになります。

式(4)

\[ \lim_{~ \Delta x \rightarrow 0} \frac{f(a + \Delta x) - f(a)}{\Delta x} \]

ここでも新しい記号 \(\lim_{~ \Delta x \rightarrow 0}\) が出てきて混乱するかもしれませんが、簡単に説明しておきましょう。

これは極限と呼ばれる操作を表し、矢印で示されている通りに式を書き換える必要があります。言葉で表現するなら \(\Delta x\) を0に近づけるということです。

この「近づける」という操作ですが、これに近いニュアンスとしては \(\Delta x \simeq 0\) にすることがあげられますね。つまり \(\Delta x\) にほぼ0に近い値を代入するという意味ですね。

※しかし、厳密にはこの解釈はの通りではないため \(\lim\) という記号があるのでしょう。実際に極限操作とは、「本来不可能なことを可能にする」という意味が含まれていたりします。例えば以下の内容で分母に0をもった量が現れますが、これは本来数学的に定義することができません。しかし、そのような表現を可能にしてくれる大切な記号です。

ところが極限の記号が示す指示通りに極限の操作 \(\Delta x \rightarrow 0\) を実行してみると、分母も分子も0に近づく事になります。

\[ \lim_{~ \Delta x \rightarrow 0} \frac{f(a + \Delta x) - f(a)}{\Delta x} \rightarrow \frac{0}{0} ~ (?) \]

計算の結果は不定形の式となり値が定まっていませんが、この手の問題は少し工夫することによって実はあるただ1つ値に収束してくれる可能性を秘めています。

もし極限の実行によって何らかの値に収束してくれるとき、その得られる値を極限値と呼ぶのですが、式(4)が極限値をもつ際は特別な記号が利用されます。

式(5)

\[ \frac{df(a)}{dx} \equiv \lim_{~ \Delta x \rightarrow 0} \frac{f(a + \Delta x) - f(a)}{\Delta x} \]

極限値である式(5)の左辺には特別に名称が与えられており、\(x = a\) における微分係数と呼ばれています。

またここで \(a\) をある区間で連続的に変化させたとして、その区間全体において微分係数が存在するならば、\(a\) を連続変数 \(x\) に置き換えた関数を定義することができそうです。

式(6)

\[ \frac{df(x)}{dx} = \lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]

この式(6)の左辺を \(f(x)\) に関する導関数と呼び、これを得るための極限の操作を微分といいます。

※式(6)の表現に違和感を覚える場合、\(\Delta x\) を \(h\) に置き換えれば一般的な数学の教科書に載っているものと同じであることが理解できます。

微分の幾何学的意味

この節の最後に、結局のところ微分とは何を表しているのかグラフを用いて理解しておきましょう。

微分とは前項までに示したきたように、ある関数 \(f(x)\) 上に取った2つの点A, Bに対して、一方の点を他方の点に限りなく近づける極限操作のことを言うのでした。

極限操作によってそれら2点を通る直線がどの様な挙動を示すのかは、以下の図を見ていただくほうが早いでしょう。

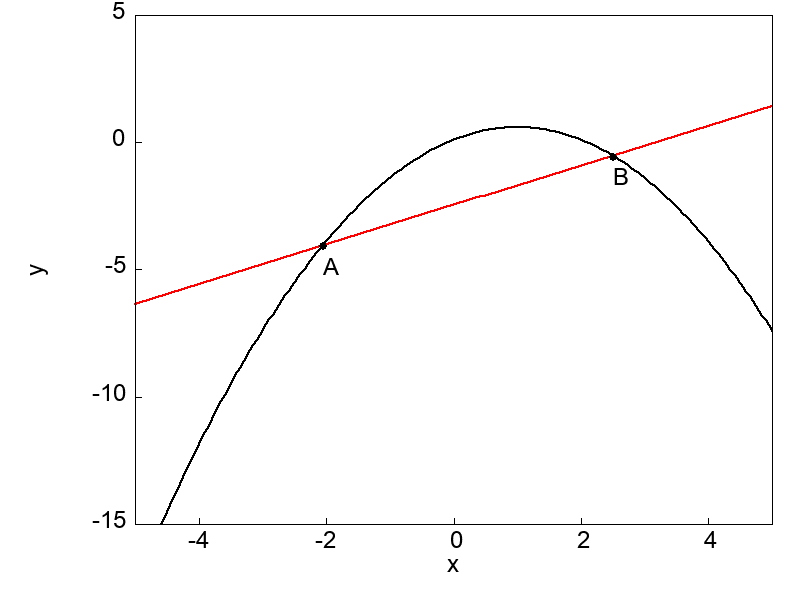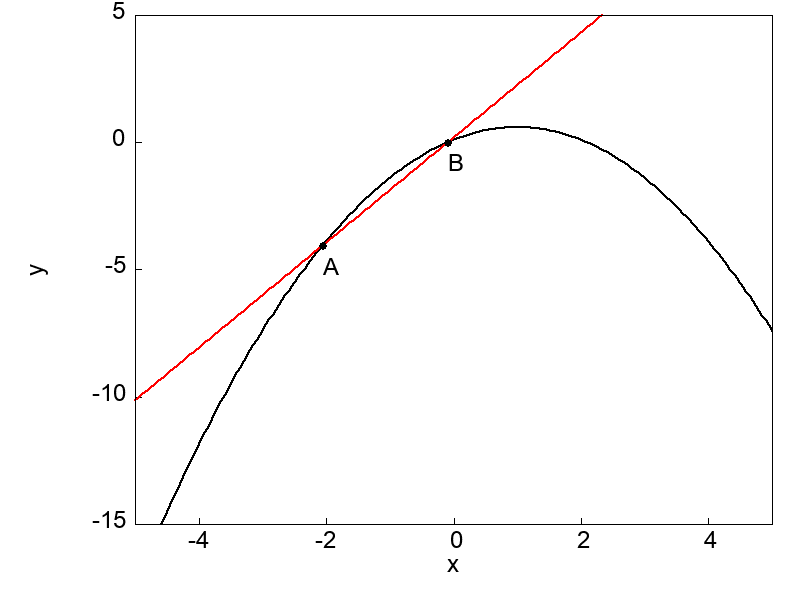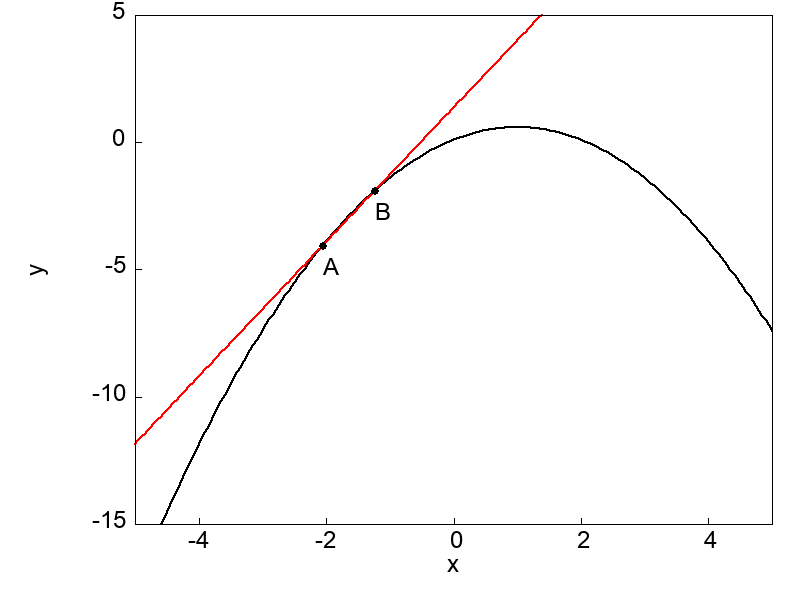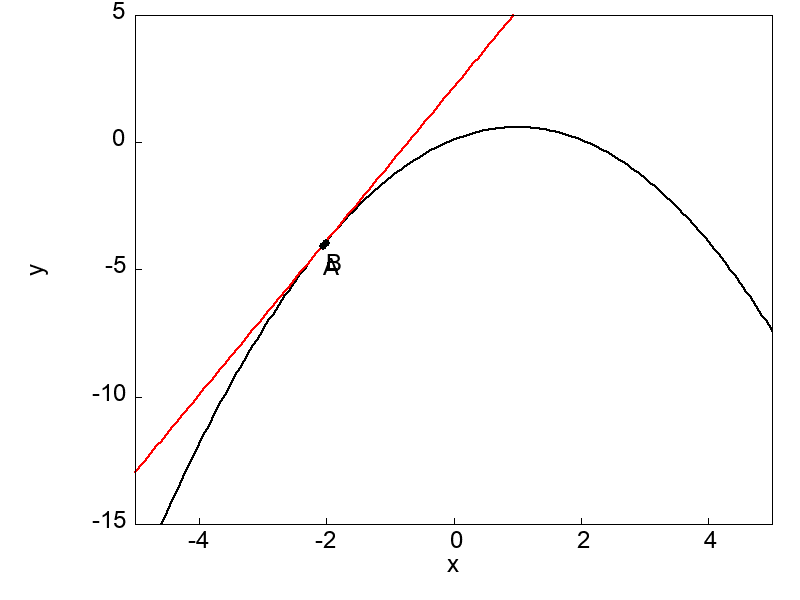
図で示したように曲線上の点Bを点Aに限りなく近づけることによって、直線はある状態に落ち着いてくる（収束する）ことが分かります。

ある状態とは点Aに接する状態のことであり、グラフ上の2点を通る直線は極限操作によって1点における接線となるのです。

本来直線は2点なければ引くことができませんが、極限という特殊な操作によって1点でも直線を引くことを可能にしてくれます。

前述した通り極限によって得られるただ1つの値のことを極限値といい、傾きの極限は特別に微分係数と言いました。

同じく接線もただ1つ求まり、点A ( \(x = a\) ) における接線の傾きこそが微分係数 \(\frac{df(a)}{dx}\) であることが理解できます。

そして接線を数学的に扱う際には微分係数を用いて次のように表現すれば良いです。

式(7)

\[ y = f(a) + \frac{df(a)}{dx}(x - a) \]

微分可能性

前節では関数を微分することによって、グラフの接線を求められることを示しました。

ところが、一般にどのような関数でも微分が可能ということではありません。

例えば、次にグラフに示すような関数は微分不可能です。

関数 \(f(x)\) は \(x = 0\) でとがった点（尖点）を持っていますが、この点こそが関数を微分不可能にさせる原因となるのです。

※とがった点の存在以外にも微分を不可能にさせる要因は様々です。例えば、ある有理関数 \(\frac{f(x)}{g(x)}\) において \(x = a\) のとき \(g(a) = 0\) となるとします。つまりその有理関数は \(x = a\) において分母が0となり定義することができないため、\(x = a\) において微分不可能となります。

とがった点が存在すると、なぜ微分が不可能であると言えるのか詳細に見ていきます。

次に示す図は \(x = 0\) における接線を求めようと微分操作を実行する過程を示したものになります。

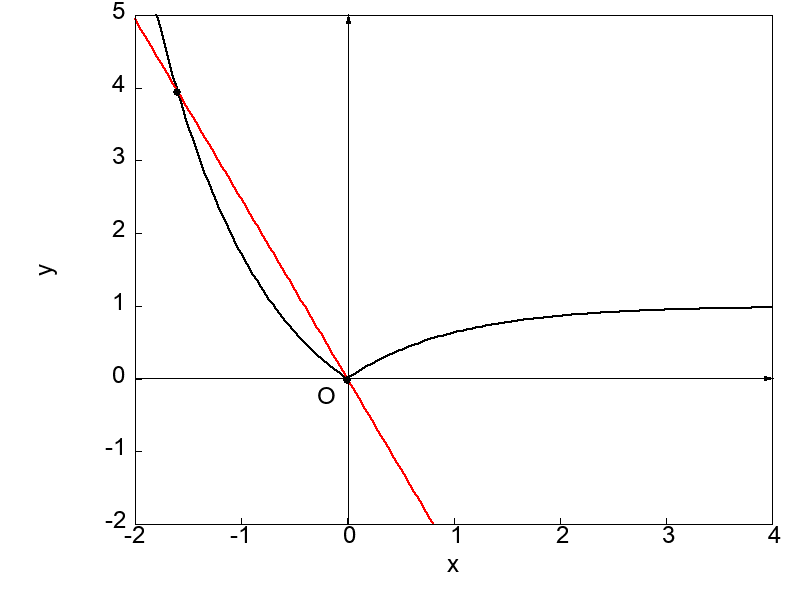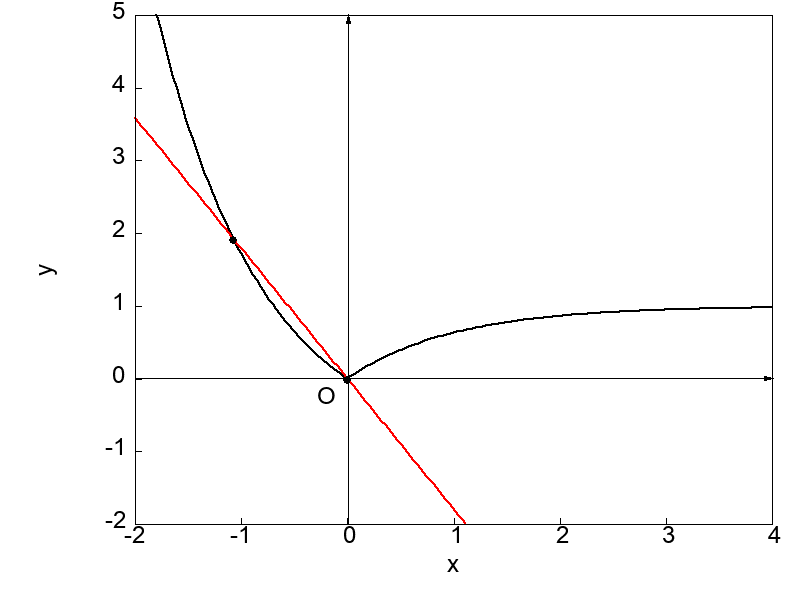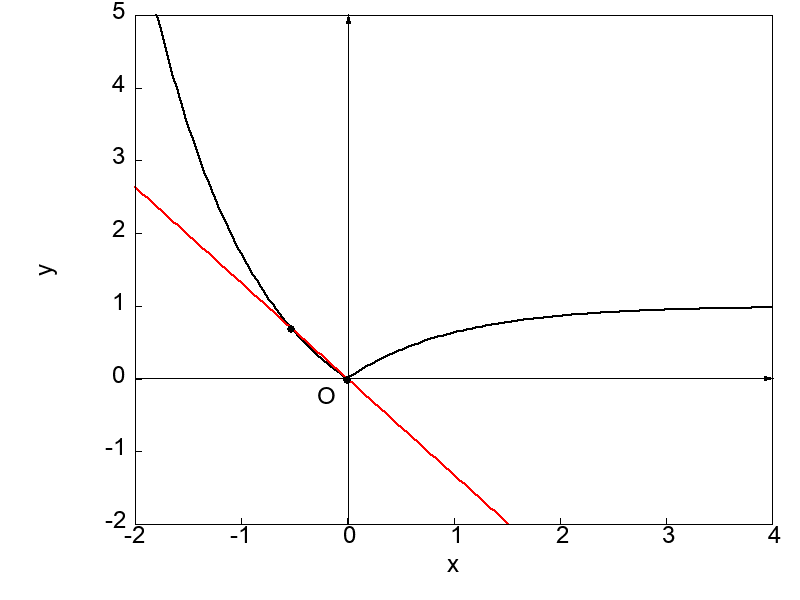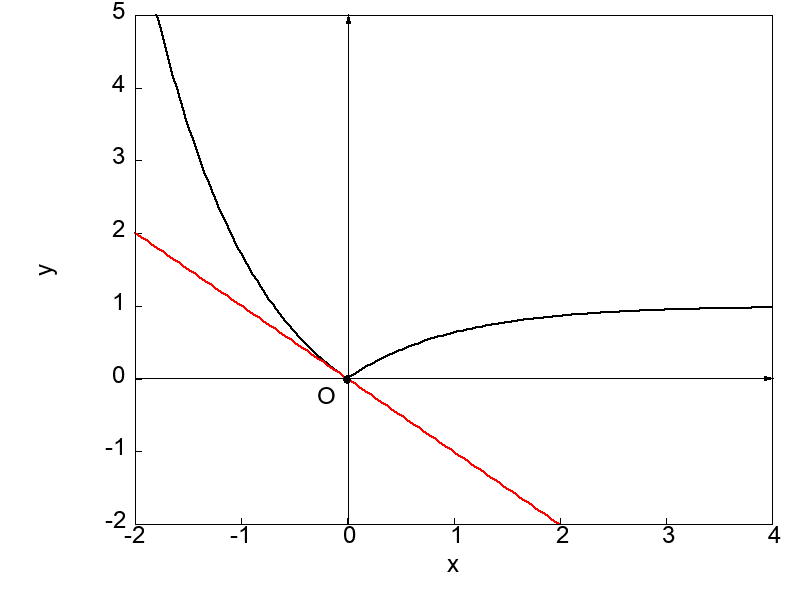
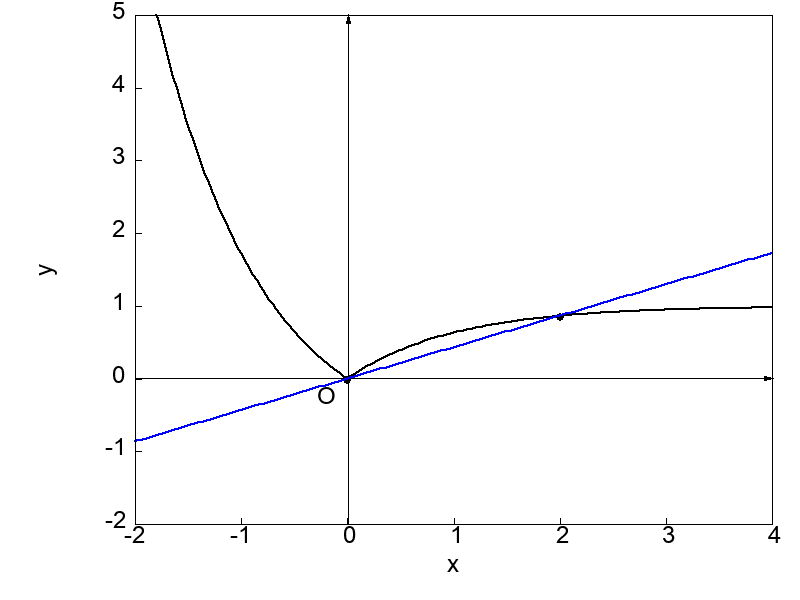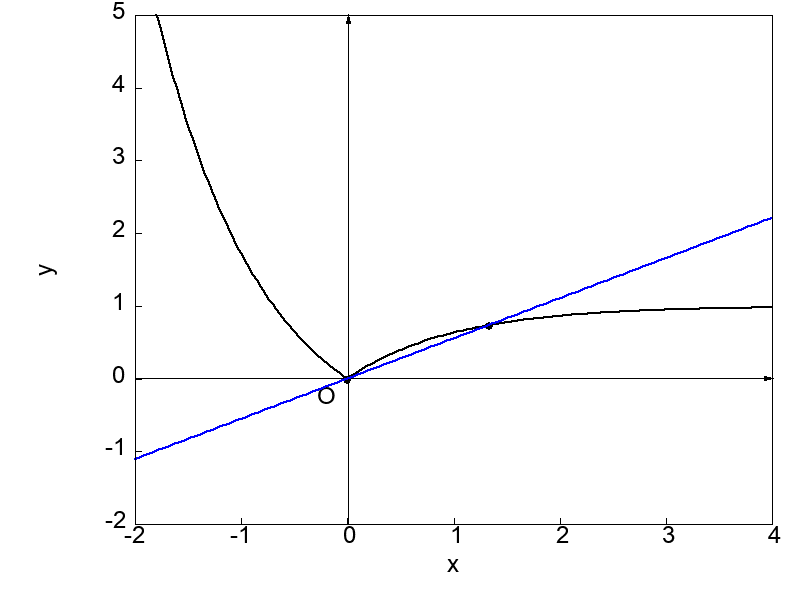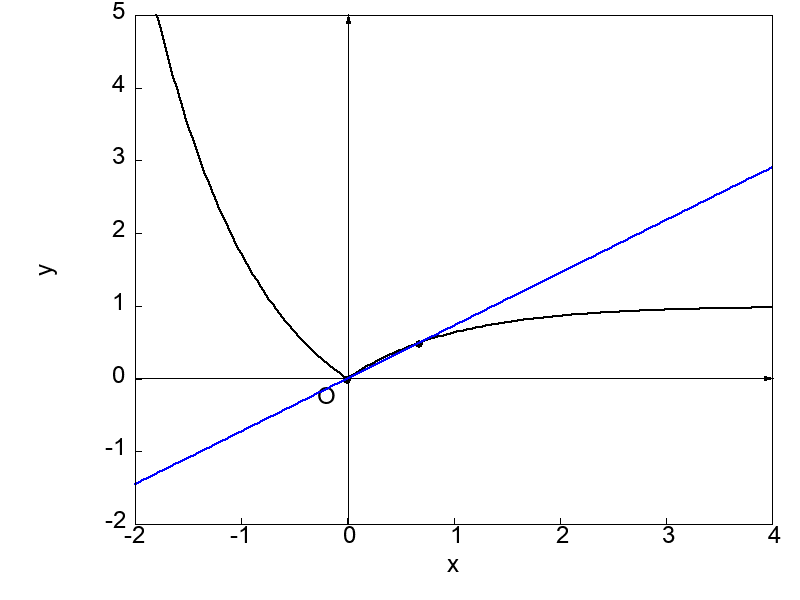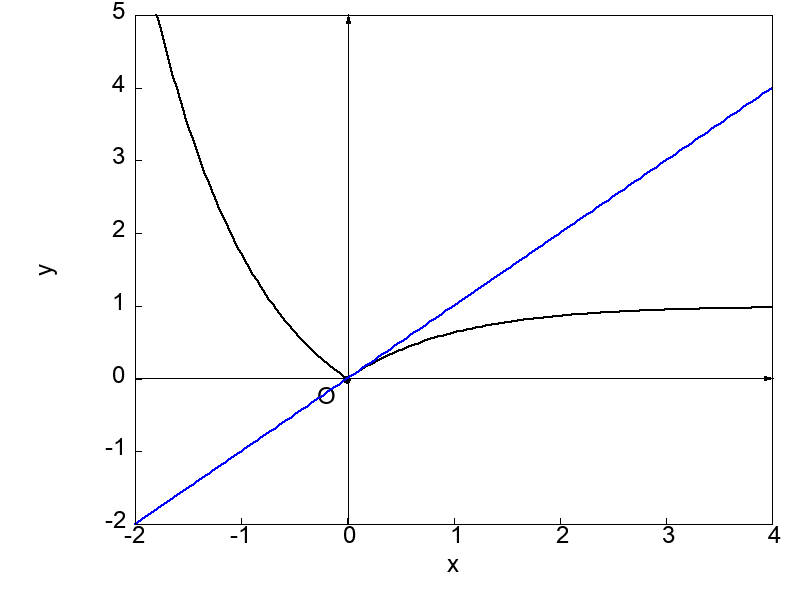
上で示した2つの図を比較すると、とがった点 \(x = 0\) に対してもう一方の点を左側および右側から近づけた場合で得られる接線が異なることが分かります。

それぞれの場合で \(x = 0\) における接線の傾きが異なるということは、微分係数が異なるということです。

つまり極限値が2通り存在するということになり、これは前節で定めた微分の定義に反します。

微分操作は、それを実行する点において微分係数が一意に定まる必要があることを思い出しましょう。

以上のように極限値である微分係数が一意に定まらない場合を微分不可能と呼びます。

逆に微分が可能な場合は、微分を実行する点において微分係数が一意に決まるということであり、数学的に表現すると次式のようにまります。

式(8)

\[ \frac{df(a)}{dx} = \lim_{\Delta x \rightarrow +0} \frac{f(a + \Delta x) - f(a)}{\Delta x} = \lim_{\Delta x \rightarrow -0} \frac{f(a + \Delta x) - f(a)}{\Delta x} \]

式(8)は点 \(x = a\) における微分係数で一般の形式で表しています。前述の関数に適用する場合 \(a = 0\) とすれば良いです。

このままでも問題ありませんが、式(8)をよく見てみると右辺には \(\Delta x \rightarrow -0\) といったように、幅を表す \(\Delta x\) に負号が付いていて少し違和感を覚えるので、\(\Delta x = x - a\) として式(8)を書き換えてみましょう。

式(9)

\[ \begin{align*} \lim_{x - a \rightarrow +0} \frac{f(x) - f(a)}{x - a} &= \lim_{x - a \rightarrow -0} \frac{f(x) - f(a)}{x - a} \\[20pt] \lim_{\textcolor{red}{x \rightarrow a + 0}} \frac{f(x) - f(a)}{x - a} &= \lim_{\textcolor{red}{x \rightarrow a - 0}} \frac{f(x) - f(a)}{x - a} \end{align*} \]

すると式(9)は先程の図で示した内容を数学的に記述できていることが分かりやすくなるでしょう。

\(a + 0\) とは点 \(a\) よりもちょっと右のことを、逆に \(a - 0\) とは点 \(a\) よりもちょっと左のことを表しています。

つまり点 \(x\) を操作して点 \(a\) よりちょっと右やちょっと左の位置まで動かすことをそれぞれ右側極限、左側極限と言い、またこれらをまとめて両側極限と呼ぶこともあります。

以上、まとめるとある点 \(x = a\) について微分が可能であるのかを判定するには両側極限を考えればよく、それらの結果が等しければ良いということになります。

ところでこの節の冒頭では「関数が微分可能であるか」という話から始まりましたが、上記で示した結果から微分可能であるか否かは関数全体の話ではなく、関数上のある点についてのみ言及していることになります。

要するに、今回例にあげた関数 \(f(x)\) は \(x = 0\) において微分が不可能であっただけであり、その他の点では微分係数が定義できることに注意する必要があります。

1点が微分不可能であるからと言って、関数全体が微分不可能であるということではありません。

微分記号の意味

ところで、式(6)の分子を \(f(x + \Delta x) - f(x)\) と表記していますが、これは前節で説明した通り \(y\) の値の変化のことであり、\(\Delta y\) あるいは \(\Delta f(x)\) と表現することができます。

式(10)

\[ \frac{df(x)}{dx} = \lim_{\Delta x \rightarrow 0} \frac{\Delta f(x)}{\Delta x} \]

左辺と右辺を見比べてみると \(\Delta x\) を0に近づけたものが \(dx\) となり、それに伴って \(\Delta f(x)\) も小さくなった結果、\(df(x)\) へと姿を変えたかのように思えます。

すると微分を表す記号 \(\frac{df(x)}{dx}\) とは「 \(dx\) 分の \(df(x)\) 」のことかと理解できそうですが、これは半分正解で半分不正解です。

というのも、この記号の読みが「ディーエフ・ディーエックス」であることから伺えるように、分数ではないということを強く主張していることが分かります。

加えて微分の記号には様々な記法があり、以下にいくつか例をあげたのでまずは見ていただくことにしましょう。

\[ \begin{align*} \frac{d}{dx}f(x) && D f(x) && f'(x) \end{align*} \]

これらはすべて関数 \(f(x)\) の \(x\) 微分、すなわち \(\frac{df(x)}{dx}\) と同じ意味をもちます。

当サイトでは上記左の \(\frac{d}{dx}f(x)\) という記法も多々利用しますが、これには「関数 \(f(x)\) に \(\frac{d}{dx}\) という操作を付け加える」という意味があります。

もう少し正確に言うと関数 \(f(x)\) に \(\frac{d}{dx}\) という命令を作用することを意味しているのです。

その命令とは、つまり「 \(x\) で微分する」ことですね。

ちなみにこの命令は数学的に演算子と呼ばれるものですが、余計に「分数」という理解からは遠く離れていってしまうかもしれません。

もちろん演算子としての扱いも重要になってきますが、数学を道具として利用する立場からして厳密な数学よりも「応用数学」の習得を第一に考えるべきです。

ハッキリ言ってしまいますが、少なくとも当サイトの範疇では常に微分は分数と見なせます。

裏を返せば \(dx\) や \(df(x)\)（または \(dy\) ）単体で扱うことが可能になるのです。

これらは、前述の通り変化量 \(\Delta x\) や \(\Delta f(x)\)（または \(\Delta y\) ）を限りなく0に近づけたことによって姿を変えたものと解釈できるため、しばしば微小量と呼ばれます。