ヘンリーの法則

揮発性の成分が溶解した溶液について成立するヘンリーの法則を紹介します。

ヘンリーの法則

溶媒に対して難溶性を示す気体成分と気液平衡状態にある系について、温度・圧力一定条件の下で次に示すヘンリーの法則が成立します。

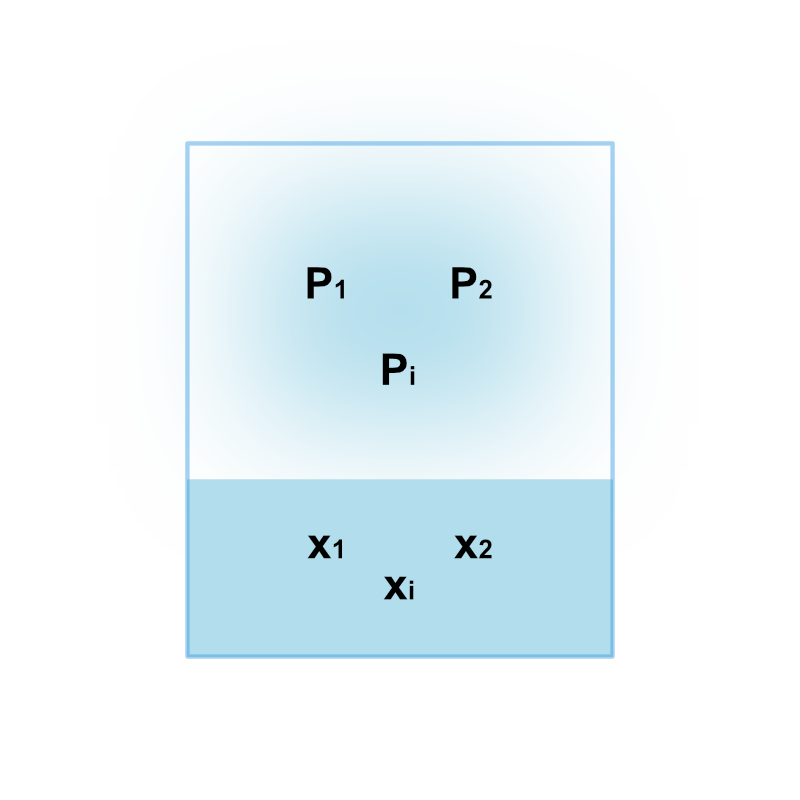
\[ x_i = H^{-1}_i P_i \]

• \(x_i\) : 成分 \(i\) の溶液中におけるモル分率
• \(P_i\) : 成分 \(i\) の気相における分圧
• \(H_i\) : 比例定数

要するにヘンリーの法則は、系に加える圧力が大きいほど気体は溶媒に溶解しやすいという事を主張しているに過ぎません。

ヘンリーの法則の導出

ヘンリーの法則は、溶媒の蒸気圧がラウールの法則にしたがう溶液についてギブス・デュエムの式から導くことができます。

\[ n^{\text{(L)}}_1 d\mu^{\text{(L)}}_1 + \sum_{i = 2}^r n^{\text{(L)}}_i d\mu^{\text{(L)}}_i = 0 ~~~ \big( ~ dT = 0, ~ dP = 0 ~ \big) \]

ここで \(n^{\text{(L)}}_i\), \(\mu^{\text{(L)}}_i ~ \big( 1 \leq i \leq r \big)\) は溶液中の成分 \(i\) の物質量および化学ポテンシャルです。また成分1を溶媒、その他 \((2 \leq i \leq r)\) を溶媒に対して難溶性を示す溶質とします。

溶媒である成分1の化学ポテンシャルは次式で与えられます。

\[ \begin{align*} \mu^{\text{(L)}}_1(T, ~ P; ~ \boldsymbol{n}) &= \mu^{\text{(L)}}_1(T, ~ P) + RT \ln \frac{P_1}{P^*_1} \\[15pt] &= \mu^{\text{(L)}}_1(T, ~ P) + RT \ln x_1 \end{align*} \]

式中の \(P^*_1\) は純粋な成分1の蒸気圧です。いま溶媒の蒸気圧はラウールの法則 \(P_1 = P^*_1 x_1\) を満たすため、対数項の圧力比 \(\frac{P_1}{P^*_1}\) は溶液中における成分1のモル分率 \(x_1\) で置き換えられます。

一方で溶質である難溶性気体の化学ポテンシャルは次式で与えられます。

\[ \mu^{\text{(L)}}_i(T, ~ P; ~ \boldsymbol{n}) = \mu^{\text{(L)}}_i(T, ~ P) + RT \ln \frac{P_i}{P^*_i} \]

溶媒1とは異なり溶質 \(i\) の蒸気圧はラウールの法則に従うかは分からず、圧力比 \(\frac{P_i}{P^*_i}\) はモル分率 \(x_i\) で置き換えられる保証はありません。

式(3), (4)を式(2)に代入して整理していくと次のようになります。

\[ \begin{align*} &\text{eq(5.1) :} ~~~~~ n^{\text{(L)}}_1 d \big\{ \mu^{\text{(L)}}_1(T, ~ P) + RT \ln x_1 \big\} + \sum_{i = 2}^r n^{\text{(L)}}_i d \left\{ \mu^{\text{(L)}}_i(T, ~ P) + RT \ln \frac{P_i}{P^*_i} \right\} = 0 \\[15pt] &\text{eq(5.2) :} ~~~~~ \Rightarrow ~ n^{\text{(L)}}_1 d \ln x_1 + \sum_{i = 2}^r n^{\text{(L)}}_i d \ln \frac{P_i}{P^*_i} = 0 \end{align*} \]

純粋な成分の化学ポテンシャル \(\mu^{\text{(L)}}_1(T, ~ P)\) および \(\mu^{\text{(L)}}_i(T, ~ P)\) は等温・定圧条件の下では定数なので、式(5)の微分計算によって消去されます。

また対数の微分が \(d\ln \text{■} = \frac{d\text{■}}{\text{{■}}}\) と書き換えられることを利用して更に式(5)の計算を進めると

\[ \begin{align*} &\text{eq(6.1) :} ~~~~~ n^{\text{(L)}}_1 \frac{dx_1}{x_1} + \sum_{i = 2}^r n^{\text{(L)}}_i \frac{d(P_i/P^*_i)}{P_i/P^*_i} = 0 \\[15pt] &\text{eq(6.2) :} ~~~~~ \Leftrightarrow ~ n^{\text{(L)}}_1 \frac{dx_1}{x_1} + \sum_{i = 2}^r n^{\text{(L)}}_i \frac{dP_i}{P_i} = 0 \\[15pt] &\text{eq(6.3) :} ~~~~~ \Leftrightarrow ~ dx_1 + \sum_{i = 2}^r x_i \frac{dP_i}{P_i} = 0 ~~~ \left( ~ x_i = \frac{n^{\text{(L)}}_i}{\sum_{i = 1}^r n^{\text{(L)}}_i} ~ \right) \end{align*} \]

となります。

溶媒のモル分率の微分 \(dx_1\) は

\[ dx_1 = d \left( 1 - \sum_{i = 2}^r x_i \right) = - \sum_{i = 2}^r dx_i \]

に等しいので、式(6.3)に代入すると次式が得られます。

\[ \sum_{i = 2}^r \left( x_i \frac{dP_i}{P_i} - dx_i \right) = 0 \]

ここで、溶質 \(i ~ (2 \leq i \leq r)\) の間でそれぞれが影響を及ぼすことなく独立に扱うことができるなら、
式(8) \(i\) 番目の項について次の関係が成立すると考えられます。

\[ x_i \frac{dP_i}{P_i} - dx_i = 0 \]

この微分方程式を解くと

\[ \begin{align*} &\text{eq(10.1) :} ~~~~~ \frac{dx_i}{x_i} = \frac{dP_i}{P_i} \\[15pt] &\text{eq(10.2) :} ~~~~~ \ln x_i = \ln P_i + \text{Const.} \\[15pt] &\text{eq(10.3) :} ~~~~~ \therefore ~ x_i = H^{-1}_i P_i \end{align*} \]

となってヘンリーの法則が得られます。ただし \(H_i\) は比例定数です。

また気相中に存在する成分 \(i\) の蒸気圧と液相中のモル分率 \(x_i\) との比例関係を表す式は、ヘンリーの法則以外で先に利用したラウールの法則も該当します。

実は理想的に振る舞う溶液では、これらは一致します。すなわち

\[ \left. \begin{align*} &\text{Henry's law : } && P_i = H_i x_i \\[15pt] &\text{Raoult's law : } && P_i = P^*_i x_i \end{align*} \right\} \Rightarrow ~ H_i = P^*_i \]

を満たします。

しかしながら一般に溶液は非理想的に振る舞うために \(H_i ~ \char`≠ ~ P^*_i\) となります。