異なる純物質どうしを混合して調製される液体を溶液と言います。

溶液の物理的性質について考察するにあたり、理想的な溶液を定義しておくと便利です。

そのような溶液を理想溶液と呼びますが、理想的な振る舞いとは具体的には何を指すのか当ページで解説していきます。

理想溶液

理想溶液とは、理想的な振る舞いをする溶液です。では「理想的」が指す具体的な内容とは一体どのようなものでしょうか。

体系を構築する上で糸口となるのは理想気体の混合による状態変化です。

温度 \(T [\text{K}]\)、圧力 \(P [\text{Pa}]\) の下で \(n_1 [\text{mol}]\) の理想気体1および \(n_2 [\text{mol}]\) の理想気体2を混合することによって、それぞれの気体の分圧が \(P_1\) および \(P_2\) となったとき、混合ギブス自由エネルギー変化 \(\Delta G_\text{mix}\) は次のように記述することができます。

\[ \Delta G_\text{mix} = RT \left( n_1 \ln \frac{P_1}{P} + n_2 \ln \frac{P_2}{P} \right) \]

熱力学的には、混合の操作は次のように表すことができ、等温・等圧条件の下において混合前後における系の体積が保存されるという特徴があります。

\[ \big(T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2)\big) ~ \xrightarrow{\text{i}} ~ (T; ~ V_1 + V_2, ~ n_1, ~ n_2) \]

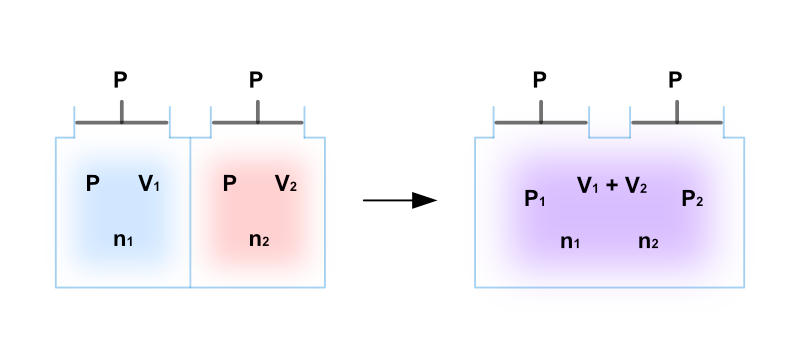
操作(1)の左辺は混合前の複合系、右辺は混合後の系の平衡状態を表しており、系全体で体積は \(V_1 + V_2\) となっています。

また矢印の上の「i」は、操作(1)による状態変化が等温過程 ( isothermal ) であることを明示するための記号です。

更に複数の物質の混合を考える事も可能で、式(1)を拡張した次式が成立します。

\[ \Delta G_\text{mix} = RT \sum_{i = 1}^r n_i \ln \frac{P_i}{P} ~~~ \left( ~ P = \sum_{i = 1}^r P_i ~ \right) \]

ここで \(P_i\) は成分 \(i\) の分圧を表しています。

理想溶液では、式(1)および式(2)に示す理想気体の混合による状態変化がそのまま適用できるものと定めます。

溶液について式(2)を適用する場合、圧力ではなく物質量を用いたほうが都合が良いです。

そこで圧力を次に示すように物質量の比で置き換えを行います。

\[ \frac{P_i}{P} \rightarrow \frac{n_i}{n} \]

式(3)を式(2)に適用すれば直ちに次式を得ることができます。

\[ \Delta G_\text{mix} = RT \sum_{i = 1}^r n_i \ln \frac{n_i}{n} \]

また溶液を構成している成分が理想気体と同様に扱えるとするなら、式(3)は次に示す2つの状態方程式から導くことが可能です。

\[ \begin{align*} \left\{ \begin{align*} ~ P_iV &= n_iRT \\[15pt] ~ PV &= nRT \end{align*} \right. &\rightarrow ~ \frac{P_iV}{PV} = \frac{n_iRT}{nRT} \\[30pt] &\Rightarrow ~ \frac{P_i}{P} = \frac{n_i}{n} \end{align*} \]

式(4)に戻って、両辺を総物質量 \(n\) で割ると

\[ \Delta \bar{G}_\text{mix} \equiv \frac{\Delta G_\text{mix}}{n} = RT \sum_{i = 1}^r \frac{n_i}{n} \ln \frac{n_i}{n} \]

となり、混合物質 1 \([\text{mol}]\) あたりの混合ギブス自由エネルギー変化 ( モル混合ギブス自由エネルギー変化 ) を得ることができます。

そして、新たに次に示すモル分率を定義します。

\[ x_i \equiv \frac{n_i}{n} \]

モル分率は、成分 \(i\) が系に何割存在するかを表す量です。

式(6)の両辺について総和を考えると

\[ \sum_{i = 1}^r x_i = \sum_{i = 1}^r \frac{n_i}{n} = 1 \]

といったように、全成分のモル分率の和は 1 となります。

このモル分率を用いれば、式(5)のモル混合ギブス自由エネルギー変化は次のように表すことができます。

\[ \Delta \bar{G}_\text{mix} = RT \sum_{i = 1}^r x_i \ln x_i \]

熱力学的に見た理想溶液の性質

混合ギブス自由エネルギー変化

理想溶液を調製する際に見られる熱力学的挙動について調べてみましょう。

簡単のために2成分系で考えることにすると、式(7)は次のようになります。

\[ \Delta \bar{G}_\text{mix} = RT \big( x_1 \ln x_1 + x_2 \ln x_2 \big) \]

いま \(x_1 + x_2 = 1\) が成立しているので、式(9)は次のように書き換えることができます。

\[ \Delta \bar{G}_\text{mix} = RT \big\{ x_1 \ln x_1 + (1 - x_1) \ln (1 - x_1) \big\} \]

後でグラフで確認しますが、任意の \(x_1\) で必ず \(\Delta \bar{G}_\text{mix} \leq 0\) となることが分かります。

つまり、理想的な状況において異なる2つの物質はどのような割合でも必ず混ざり合う事になります。

混合エントロピー変化

ギブス自由エネルギーが分かっていればエントロピーは次式から得ることが可能です。

\[ \left( \frac{\partial G}{\partial T} \right)_{P, ~ \boldsymbol{n}} = -S \]

式(11)を用いれば、モル混合エントロピー変化 \(\Delta \bar{S}_\text{mix}\) は次のように導かれます。

\[ \Delta \bar{S}_\text{mix} = -\left( \frac{\partial \Delta \bar{G}_\text{mix}}{\partial T} \right)_{P, ~ \boldsymbol{n}} = -R \big\{ x_1 \ln x_1 + (1 - x_1) \ln (1 - x_1) \big\} \]

式(12)から任意の \(x_1\) で \(\Delta \bar{S}_\text{mix} \geq 0\) となることが分かります。

前項の結果 \(\Delta \bar{G}_\text{mix} \leq 0\) から理解される事と同じく、理想的な混合では異なる2つの物質をどのような割合で混ぜたとしてもエントロピーは増加し混ざり合うことになります。

混合内部エネルギー変化

ここまでの内容を利用して、モル混合内部エネルギー変化は 0 になることを示すことができます。

内部エネルギーはギブス自由エネルギーの定義から

\[ U = G - PV + TS \]

で与えられます。

いま系は等温・等圧条件下にあることに注意して、式(13)からモル混合内部エネルギー変化 \(\Delta \bar{U}_\text{mix}\) を求めると

\[ \Delta \bar{U}_\text{mix} = \Delta \bar{G}_\text{mix} - P \Delta \bar{V}_\text{mix} + T \Delta \bar{S}_\text{mix} \]

となります。

理想的な状況では、混合の前後で系の体積変化は生じないため \(\Delta \bar{V}_\text{mix} = 0\) です。

また式(14)に、式(10)および式(12)を代入すると

\[ \begin{gather*} \Delta \bar{U}_\text{mix} = RT \big\{ x_1 \ln x_1 + (1 - x_1) \ln (1 - x_1) \big\} - RT \big\{ x_1 \ln x_1 + (1 - x_1) \ln (1 - x_1) \big\} \\[15pt] \therefore ~ \Delta \bar{U}_\text{mix} = 0 \end{gather*} \]

このとおり、モル混合内部エネルギー変化が 0 となることが分かります。

混合ヘルムホルツ自由エネルギー変化

混合によるヘルムホルツ自由エネルギー変化はどのように記述されるでしょうか。

ヘルムホルツ自由エネルギーは、ギブス自由エネルギーを用いて \(F = G - PV\) と表すことができます。

この事から、モル混合ヘルムホルツ自由エネルギーを \(\Delta \bar{F}_\text{mix}\) とすると、圧力が一定であることに注意して

\[ \Delta \bar{F}_\text{mix} = \Delta \bar{G}_\text{mix} - P \Delta \bar{V}_\text{mix} \]

となります。

理想混合では体積変化がなく \(\Delta \bar{V}_\text{mix} = 0\) であるから

\[ \Delta \bar{F}_\text{mix} = \Delta \bar{G}_\text{mix} = RT \sum_{i = 1}^r x_i \ln x_i \]

が導かれます。

理想混合を表したグラフ

ここまでに確認してきた熱力学的挙動を1つのグラフに表したものが次図になります。

モル混合内部エネルギー変化 \(\Delta \bar{U}_\text{mix}\) を表した曲線は、グラフ横軸と完全に一致しています。

これは理想的な状況において、異なる2つの物質を混合するとき、どのような割合で混ぜ合わせても内部エネルギーの変化は生じないことを表しています。

その他、モル混合自由エネルギー変化 \(\Delta \bar{G}_\text{mix}\) とモル混合エントロピー変化 \(T\Delta \bar{S}_\text{mix}\) を表したグラフは、横軸に対して対称に描かれます。

\(\Delta \bar{G}_\text{mix}\) は任意の \(x_1\) で 0 以下の値を取り、\(T\Delta \bar{S}_\text{mix}\) は任意の \(x_1\) で 0 以上の値を取ります。

前述の繰り返しになりますが、理想混合では異なる2つの物質はどのような割合でも必ず混ざり合う事を表しています。