複数の成分を含む系、多成分系は、純粋な物質同士を混合することで形成されます。

当ページでは理想気体の混合による系の状態変化についてエネルギーの観点から理解することを目指します。

以下では、混合によるエネルギー変化やエントロピー変化の詳細を確認する前に、実験事実として混合気体について成立する法則を最初に示すことにします。

混合気体の法則

複数の理想気体を混合して得られる混合気体について成立する重要な法則2つを紹介します。

• アマガーの法則 ( 体積に関する和の法則 )
• ドルトンの法則 ( 圧力に関する和の法則 )

それぞれ説明していきます。

アマガーの法則

アマガーの法則とは温度・圧力一定の条件下で複数種の理想気体を混合させたとき、混合気体の体積は混合前の気体の体積の和になるという実験事実を説明する法則です。

温度 \(T\)、圧力 \(P\) の下で混合前のそれぞれの理想気体の物質量を \(n_1\), \(n_2\), \(\cdots\), \(n_r\)、また体積を \(V_i ~ ( ~ 1 \leq i \leq r ~ )\) とすると、理想気体の状態方程式から下記が成立します。

\[ \begin{gather*} P V_1 = n_1 RT \\[15pt] P V_2 = n_2 RT \\[15pt] \vdots \\[15pt] P V_r = n_r RT \end{gather*} \]

混合気体の総物質量を \(n = \sum_{i = 1}^r n_i\) として式(1) \(PV_i = n_iRT\) を代入すると次式が得られます。

\[ n = \frac{P}{RT} \sum_{i = 1}^r V_i \]

理想気体どうしを混合しても理想性を失わないとすると、混合気体も同様に理想気体の状態方程式 \(PV = nRT\) を満たすので、次に示すように混合気体の体積 \(V\) は混合前のそれぞれの理想気体の体積の和で表されることが分かります。

\[ V = \sum_{i = 1}^r V_i \]

これがアマガーの法則です。

また式(3)は、式(1)の両辺を足し合わせることでも導出可能であると分かります。

\[ P (V_1 + V_2 + \cdots + V_r) = (n_1 + n_2 + \cdots + n_r)RT \]

また \(V_i\) は混合気体の体積 \(V\) と物質量から求めることが可能で、成分 \(i\) について成立する状態方程式 \(PV_i = n_iRT\) と 混合気体で成立する状態方程式 \(PV = nRT\) を両辺で割って整理すれば

\[ \begin{gather*} \frac{V_i}{V} = \frac{n_i}{n} \\[20pt] \therefore ~ V_i = \frac{n_i}{n} V \end{gather*} \]

となります。

ドルトンの分圧の法則

ドルトンの法則とは温度・体積一定の条件下で複数種の理想気体を混合させたとき、混合気体の圧力は混合前の気体の圧力の和になるという実験結果を説明する法則です。

温度 \(T\)、体積 \(V\) の下で混合前のそれぞれの理想気体の物質量を \(n_1\), \(n_2\), \(\cdots\), \(n_r\)、また圧力を \(P_i ~ ( ~ 1 \leq i \leq r ~ )\) とすると、理想気体の状態方程式から下記が成立します。

\[ \begin{gather*} P_1 V = n_1 RT \\[15pt] P_2 V = n_2 RT \\[15pt] \vdots \\[15pt] P_r V = n_r RT \end{gather*} \]

混合気体の総物質量を \(n = \sum_{i = 1}^r n_i\) として式(5) \(P_iV = n_iRT\) を代入すると次式が得られます。

\[ n = \frac{V}{RT} \sum_{i = 1}^r P_i \]

理想気体どうしを混合しても理想性を失わないとすると、混合気体も同様に理想気体の状態方程式 \(PV = nRT\) を満たすので、次に示すように混合気体の圧力 \(P\) は混合前のそれぞれの理想気体の圧力の和で表されることが分かります。

\[ P = \sum_{i = 1}^r P_i \]

これがドルトンの法則です。

また式(7)は、式(5)の両辺を足し合わせることでも導出可能であると分かります。

\[ (P_1 + P_2 + \cdots + P_r)V = (n_1 + n_2 + \cdots + n_r)RT \]

混合気体の場合はその圧力 \(P\) を全圧、混合気体を構成する各種気体の圧力 \(P_i\) を成分 \(i\) の分圧と呼びます。

分圧は全圧を用いて表現することが可能で、成分 \(i\) について成立する状態方程式 \(P_iV = n_iRT\) および混合気体で成立する状態方程式 \(PV = nRT\) を両辺で割って整理すれば次式を得ることができます。

\[ \begin{gather*} \frac{P_i}{P} = \frac{n_i}{n} \\[20pt] \therefore ~ P_i = \frac{n_i}{n} P \end{gather*} \]

混合の記述

混合操作

熱力学的に「混合」を記述していきましょう。

例えば、次の図に示すように、体積 \(V\) の容器を透熱性の仕切りで2つに分け、\(V_1\), \(V_2\) の空間を作るとします。

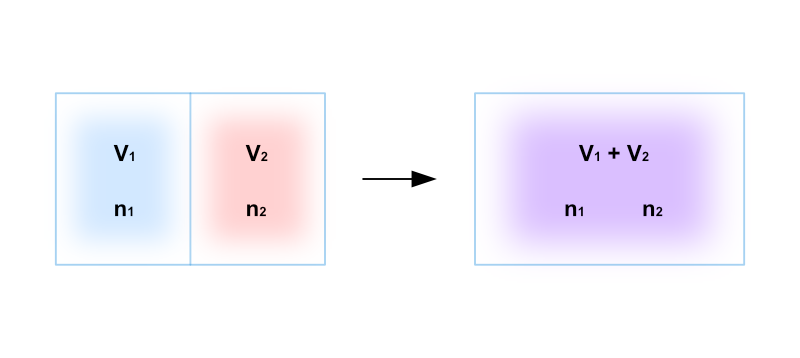
またそれぞれの空間に物質量 \(n_1\)、\(n_2\) の異なる理想気体を封入しておきます。

この状態から仕切りを取り外せば、それぞれの理想気体は容器全体に行き渡り最終的には混合状態に到達します。

混合による系の状態変化を次のように記述することにします。

\[ \big( T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2) \big) ~ \xrightarrow{\text{i}} ~ (T; ~ V_1 + V_2, ~ n_1, ~ n_2) \]

左辺は混合前の状態で、\((T; ~ V_1, ~ n_1)\) の状態および \((T; ~ V_2, ~ n_2)\) の状態にある部分系の複合状態を表します。対して右辺が混合状態を表しています。

ここで注意したいのは、混合状態は \((T; ~ V_1 + V_2, ~ \textcolor{red}{n_1 + n_2})\) という表記にならない事です。

\((T; ~ V_1 + V_2, ~ n_1, ~ n_2)\) は成分1および成分2が体積 \(V_1 + V_2\) の容器内にそれぞれ \(n_1\), \(n_2\) だけ存在することを意味しますが、

\((T; ~ V_1 + V_2, ~ n_1 + n_2)\) は体積 \(V_1 + V_2\) の容器内に1種類の成分が \(n_1 + n_2\) だけ存在することになり意味が全く異なります。

また更に成分数を増やした場合の混合操作も同様に書くことができます。

\[ \big( T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2), ~ \cdots ~ , ~ (V_r, ~ n_r) \big) ~ \xrightarrow{\text{i}} ~ (T; ~ V_1 + V_2 + \cdots + V_r, ~ n_1, ~ n_2, ~ \cdots ~ , ~ n_r) \]

ただ煩雑な記述となるので、混合後の体積を \(V = V_1 + V_2 + \cdots + V_r\)、物質量の組を \(\boldsymbol{n} = (n_1, ~ n_2, ~ \cdots ~ , ~ n_r)\) とすると次のようになります。

\[ \big( T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2), ~ \cdots ~ , ~ (V_r, ~ n_r) \big) ~ \xrightarrow{\text{i}} ~ (T; ~ V, ~ \boldsymbol{n}) \]

混合状態の熱力学量

混合気体が理想的に振る舞う場合、それに関する熱力学量が混合前の気体の熱力学量の和になることを説明します。

前節で説明したドルトンの法則をより詳細に記述した次式から始めましょう。

\[ P(T; ~ V, ~ \boldsymbol{n}) = \sum_{i = 1}^r P_i(T; ~ V, ~ n_i) \]

式(9)をヘルムホルツ自由エネルギーを用いて表現することを考えます。

圧力はヘルムホルツ自由エネルギーの体積に関する偏微分係数として表現できるので

\[ \begin{align*} P(T; ~ V, ~ \boldsymbol{n}) &= - \sum_{i = 1}^r \left( \frac{\partial F_i}{\partial V} \right)_{T, ~ n_i} \\[15pt] &= - \left( \frac{\partial}{\partial V} \sum_{i = 1}^r F_i(T; ~ V, ~ n_i) \right)_{T, ~ \boldsymbol{n}} \end{align*} \]

となります。

また混合系のヘルムホルツ自由エネルギー \(F(T; ~ V, ~ \boldsymbol{n})\) を体積で微分すれば系の圧力 \(P(T; ~ V, ~ \boldsymbol{n})\) が得られるので次式が成立します。

\[ P(T; ~ V, ~ \boldsymbol{n}) = - \left( \frac{\partial F(T; ~ V, ~ \boldsymbol{n})}{\partial V} \right)_{T, ~ \boldsymbol{n}} \]

式(10)および式(11)から、混合気体のヘルムホルツ自由エネルギーが混合前の気体のヘルムホルツ自由エネルギー \(F_i\) の和で表現可能とすると上記の内容を満足させられるでしょう。

\[ F(T; ~ V, ~ \boldsymbol{n}) \equiv \sum_{i = 1}^r F_i(T; ~ V, ~ n_i) \]

ドルトンの法則は理想気体について成立することを忘れてはなりません。

つまり式(12)も混合気体が理想的に振る舞うことが前提となっていることに注意する必要があります。

混合気体が理想的に振る舞う場合、式(12)を用いて混合気体のエントロピーや混合気体中の成分 \(i\) における化学ポテンシャルも直ちに導くことができます。

エントロピーはヘルムホルツ自由エネルギーを温度について偏微分することで得られるので

\[ \begin{align*} \left( \frac{\partial F}{\partial T} \right)_{V, ~ \boldsymbol{n}} &= \left( \frac{\partial}{\partial T} \sum_{i = 1}^r F_i(T; ~ V, ~ n_i) \right)_{V, ~ \boldsymbol{n}} \\[15pt] &= \sum_{i = 1}^r \left( \frac{\partial F_i}{\partial T} \right)_{V, ~ n_i} \\[20pt] \therefore ~ S(T; ~ V, ~ \boldsymbol{n}) &= \sum_{i = 1}^r S_i(T; ~ V, ~ n_i) \end{align*} \]

となって、混合気体のエントロピーは、各成分のエントロピーの和として表現できることが分かりました。

また、化学ポテンシャルはヘルムホルツ自由エネルギーを物質量について偏微分することで得られるので

\[ \begin{align*} \left( \frac{\partial F}{\partial n_i} \right)_{T, ~ V, ~ n_{j\char`≠i}} &= \left( \frac{\partial}{\partial n_i} \sum_{i = 1}^r F_i(T; ~ V, ~ n_i) \right)_{T, ~ V} \\[15pt] &= \sum_{i = 1}^r \left( \frac{\partial F_i}{\partial n_i} \right)_{T, ~ V} \\[20pt] \therefore ~ \mu_i(T; ~ V, ~ \boldsymbol{n}) &= \mu^*_i(T; ~ V, ~ n_i) \end{align*} \]

となります。

右辺の「*」は、混合物ではない純粋な状態の化学ポテンシャルであることを明示する場合に利用される記号です。

ただし繰り返しになりますが、上記混合系におけるエントロピーおよび化学ポテンシャルの関係は混合気体が理想的に振る舞う場合について言えるものです。

とは言え、実際に存在する系も理想的に振る舞う場合も少なくはなく、これらの関係はよく利用される重要な関係式です。

混合による系の状態変化

ここからは混合によって系の状態がどのように変化するのか、エネルギーとエントロピーの視点から説明します。

混合ヘルムホルツ自由エネルギー変化

理想気体を混合する際のヘルムホルツ自由エネルギー変化を求めましょう。

操作(3)によって生じるヘルムホルツ自由エネルギー変化 \(\Delta F\) は次式で表すことができます。

\[ \Delta F_{\text{mix}} = F(T; ~ V, ~ \boldsymbol{n}) - F\big( T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2), ~ \cdots ~ , ~ (V_r, ~ n_r) \big) \]

右辺第1項は式(12)を用いて置き換えることができます。

右辺第2項はヘルムホルツ自由エネルギーの相加性から、混合前の各気体の状態 \((T; ~ V_i, ~ n_i)\) におけるヘルムホルツ自由エネルギーの和で表現できます。

\[ F\big( T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2), ~ \cdots ~ , ~ (V_r, ~ n_r) \big) = \sum_{i = 1}^r F_i(T; ~ V_i, ~ n_i) \]

したがって混合によるヘルムホルツ自由エネルギー変化の式(15)は次のように書き換えられます。

\[ \begin{align*} \Delta F_{\text{mix}} &= \sum_{i = 1}^r F_i(T; ~ V, ~ n_i) - \sum_{i = 1}^r F_i(T; ~ V_i, ~ n_i) \\[15pt] &= \sum_{i = 1}^r \big\{ F_i(T; ~ \textcolor{red}{V}, ~ n_i) - F_i(T; ~ \textcolor{red}{V_i}, ~ n_i) \big\} \end{align*} \]

式(17)中のヘルムホルツ自由エネルギー差は、変数に着目すると異なるのは体積のみです。

これはちょうど成分 \(i\) の体積が \(V_i\) から \(V\) に変化する場合の等温最大仕事で書き換えることができるので

\[ F_i(T; ~ V, ~ n_i) - F_i(T; ~ V_i, ~ n_i) = -n_iRT \ln \frac{V}{V_i} \]

となるので、式(17)に戻して整理すれば混合ヘルムホルツ自由エネルギー変化として次式が得られます。

\[ \Delta F_{\text{mix}} = - RT \sum_{i = 1}^r n_i \ln \frac{V}{V_i} < 0 \]

また得られたヘルムホルツ自由エネルギー変化は負の値となることから、理想気体の混合が自発的に起こることが分かります。

また更に興味深いのは、理想気体の混合によるヘルムホルツ自由エネルギー変化がそれぞれの気体の体積変化のみに依存すること

理想気体の混合では混合されるそれぞれの成分による影響はありません

混合内部エネルギー変化

続いて、理想気体を混合する際の内部エネルギー変化を求めていきます。

操作(3)による内部エネルギー変化は次のとおり。

\[ \Delta U_{\text{mix}} = U(T; ~ V, ~ \boldsymbol{n}) - U\big( T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2) ~ \cdots ~ (V_r, ~ n_r) \big) \]

式(20)右辺の第2項は内部エネルギーの相加性から、混合前の各気体の状態 \((T; ~ V_i, ~ n_i)\) における内部エネルギーの和で表現できます。

\[ U\big( T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2) ~ \cdots ~ (V_r, ~ n_r) \big) = \sum_{i = 1}^r U_i(T; ~ V_i, ~ n_i) \]

したがって式(20)は次のようになります。

\[ \Delta U_{\text{mix}} = U(T; ~ V, ~ \boldsymbol{n}) - \sum_{i = 1}^r U_i(T; ~ V_i, ~ n_i) \]

多成分系における内部エネルギー \(U(T; ~ V, ~ \boldsymbol{n})\) は、前節ですでに得ている多成分系のヘルムホルツ自由エネルギーとエントロピーから導くことができます。

内部エネルギーとヘルムホルツ自由エネルギーおよびエントロピーの間には \(U = F + TS\) が成立するので、多成分系の内部エネルギーは

\[ U(T; ~ V, ~ \boldsymbol{n}) = F(T; ~ V, ~ \boldsymbol{n}) + TS(T; ~ V, ~ \boldsymbol{n}) \]

で与えられます。

混合気体が理想的に振る舞う場合は、式(12)および式(13)で示した通り多成分系のヘルム穂ツル自由エネルギーとエントロピーは各成分の和で表すことができるので

\[ \begin{align*} U(T; ~ V, ~ \boldsymbol{n}) &= \sum_{i = 1}^r F_i(T; ~ V, ~ n_i) + T \sum_{i = 1}^r S_i(T; ~ V, ~ n_i) \\[15pt] &= \sum_{i = 1}^r \big\{ F_i(T; ~ V, ~ n_i) + T S_i(T; ~ V, ~ n_i)\big\} \end{align*} \]

とできます。

また成分 \(i\) のみに着目したとき、内部エネルギーおよびヘルムホルツ自由エネルギー、エントロピーの関係として次式が成立します。

\[ F_i(T; ~ V, ~ n_i) + TS_i(T; ~ V, ~ n_i) = U_i(T; ~ V, ~ n_i) \]

以上から式(25)を式(24)に代入すれば、多成分系の内部エネルギーを得ることができます。

\[ U(T; ~ V, ~ \boldsymbol{n}) = \sum_{i = 1}^r U_i(T; ~ V, ~ n_i) \]

式(25)を式(22)に代入して整理すると

\[ \begin{align*} \Delta U_{\text{mix}} &= \sum_{i = 1}^r U_i(T; ~ V, ~ n_i) - \sum_{i = 1}^r U_i(T; ~ V_i, ~ n_i) \\[15pt] &= \sum_{i = 1}^r \big\{ U_i(T; ~ \textcolor{red}{V}, ~ n_i) - U_i(T; ~ \textcolor{red}{V_i}, ~ n_i) \big\} \end{align*} \]

式中の内部エネルギー差は、体積のみ変数が異なるので内部エネルギーの体積に関する偏微分係数の積分として次のように書き換えられます。

\[ \Delta U_\text{mix} = \sum_{i = 1}^r \int_{V_i}^V \left( \frac{\partial U_i}{\partial V} \right)_{T, ~ n_i} dV \]

理想気体の場合、温度および物質量が一定であればこの偏微分係数は 0 となるので、直ちに混合による内部エネルギー変化の計算結果も 0 になることも分かります。

\[ \therefore ~ \Delta U_{\text{mix}} = 0 \]

また式(25), (27), (29)から、次の関係を得ることもできます。

\[ U(T; ~ V, ~ \boldsymbol{n}) = \sum_{i = 1}^r U_i(T; ~ V, ~ n_i) = \sum_{i = 1}^r U_i(T; ~ V_i, ~ n_i) \]

混合エントロピー変化

理想気体の混合エントロピー変化を求めていきます。

手続きは前節までと同様に ( 統一させて ) 次式のようになります。

\[ \Delta S_{\text{mix}} = S(T; ~ V, ~ \boldsymbol{n}) - S\big(T; (V_1, ~ n_1), ~ (V_2, ~ n_2) ~ \cdots ~ (V_r, ~ n_r)\big) \]

式(31)右辺の第1項である多成分系のエントロピーは式(13)によって置き換え可能で、

第2項の混合前の状態のエントロピーはその相加性から成分ごとの和で表現できます。

\[ S\big(T; (V_1, ~ n_1), ~ (V_2, ~ n_2) ~ \cdots ~ (V_r, ~ n_r)\big) = \sum_{i = 1}^r S_i(T; ~ V_i, ~ n_i) \]

したがって混合エントロピーは次のようになります。

\[ \Delta S_{\text{mix}} = \sum_{i = 1}^r \big\{ S_i(T; ~ V, ~ n_i) - S_i(T; ~ V_i, ~ n_i) \big\} \]

右辺は成分 \(i\) が体積 \(V_i\) から \(V\) に変化するときのエントロピー変化を表し、

\[ S_i(T; ~ V, ~ n_i) - S_i(T; ~ V_i, ~ n_i) = n_i R \ln \frac{V}{V_i} \]

で与えられるので、混合エントロピー変化は次式として得られることが分かります。

\[ \Delta S_{\text{mix}} = R \sum_{i = 1}^r n_i \ln \frac{V}{V_i} > 0 \]

混合エントロピーの計算結果からもその値は正の値をとることから、混合が自発的に進むことが分かります。

混合ギブス自由エネルギー変化

理想気体の混合によるギブス自由エネルギー変化を計算してみましょう。

混合ギブス自由エネルギーは次式で表されます。

\[ \Delta G_{\text{mix}} = G(T; ~ V, ~ \boldsymbol{n}) - G\big( T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2), ~ \cdots ~ (V_r, ~ n_r) \big) \]

式(36)右辺の第2項は、ギブス自由エネルギーの相加性によって各成分の和で表現できるので

\[ G\big( T; ~ (V_1, ~ n_1), ~ (V_2, ~ n_2), ~ \cdots ~ (V_r, ~ n_r) \big) = \sum_{i = 1}^r G_i(T; ~ V_i, ~ n_i) \]

したがって、混合ギブス自由エネルギーは次式のようになります。

\[ \Delta G_{\text{mix}} = G(T; ~ V, ~ \boldsymbol{n}) - \sum_{i = 1}^r G_i(T; ~ V_i, ~ n_i) \]

ギブス自由エネルギーは温度、圧力、物質量を制御変数としたとき完全な熱力学関数となって扱いやすくなるのでした。

式(38)からは体積 \(V\), \(V_i\) を消去して圧力に置き換えたいので、気体の体積が温度、圧力、物質量を定めれば一意に決まることから \(V = V(T, ~ P; ~ n)\) のように記述して

\[ \begin{align*} & G\big(T; ~ V(T, ~ P; ~ \boldsymbol{n}) ~ \boldsymbol{n} \big) \equiv G(T, ~ P; ~ \boldsymbol{n}) \\[15pt] & G_i\big( T; ~ V_i(T, ~ P; ~ n_i) ~ n_i \big) \equiv G_i(T, ~ P; ~ n_i) \end{align*} \]

と書くことができます。

ただし、それぞれ \(PV = nRT ~ ( ~ n = \sum_{i = 1}^r n_i ~ )\) および \(PV_i = n_iRT\) の関係を元に変数を置き換えていることに注意です。

以上から式(39)は \((T; ~ V, ~ n)\) 表示から、次のように \((T, ~ P; ~ n)\) 表示に置き換えた表式にできます。

\[ \Delta G_{\text{mix}} = G(T, ~ P; ~ \boldsymbol{n}) - \sum_{i = 1}^r G_i(T, ~ P; ~ n_i) \]

多成分系における内部エネルギーやエントロピーが成分ごとの和で表現できたのと同様に、多成分系におけるギブス自由エネルギーも和を用いて表現できます。

ギブス自由エネルギーの定義式 \(G = U + PV - TS\) から多成分系では次式が成立します。

\[ G(T, ~ P; ~ \boldsymbol{n}) = U(T, ~ P; ~ \boldsymbol{n}) + PV(T, ~ P; ~ \boldsymbol{n}) - TS(T, ~ P; ~ \boldsymbol{n}) \]

既に示した通り多成分系の内部エネルギー、エントロピー、体積は各成分の和で置き換えることができます。

\[ \begin{align*} &\text{eq(30) : } && U(T; ~ V, ~ \boldsymbol{n}) = \sum_{i = 1}^r U_i(T; ~ V, ~ n_i) = \sum_{i = 1}^r U_i(T; ~ V_i, ~ n_i) \\[15pt] &\text{eq(13) : } && S(T; ~ V, ~ \boldsymbol{n}) = \sum_{i = 1}^r S_i(T; ~ V, ~ n_i) \\[15pt] &\text{eq(3) : } && V(T, ~ P; ~ \boldsymbol{n}) = \sum_{i = 1}^r V_i(T, ~ P; ~ n_i) \end{align*} \]

これらを用いればギブス自由エネルギーが各成分の和で表現できそうであることは想像に容易いです。

ところが…実際これらをそのまま式(41)に代入することはできません。

熱力学量の変数を 温度、圧力、物質量 表示 に揃える必要があります。

幸いにも体積 \(V(T, ~ P; ~ \boldsymbol{n})\) については要件を満たしているので問題ありません。

内部エネルギーとエントロピーについて変数の置き換えを行うと次の関係式を得ることができます。

\[ U(T, ~ P; ~ \boldsymbol{n}) = \sum_{i = 1}^r U_i(T, ~ P; ~ n_i) \]

\[ S(T, ~ P; ~ \boldsymbol{n}) = \sum_{i = 1}^r S_i(T, ~ \textcolor{red}{P_i}; ~ n_i) \]

着目すべきは式(43)のエントロピーでは \(P_i\) という圧力が現れることで、これは成分 \(i\) が \(V\) の体積を持つときの圧力を表します。

そして \(P_i\) は混合気体の分圧にも等しい量であることが分かるでしょう。

では、以下で式(42)および式(43)の導出をしていきます。

内部エネルギー

多成分系の内部エネルギーの式(30)を再掲します。

\[ U(T; ~ V, ~ \boldsymbol{n}) = \sum_{i = 1}^r U_i(T; ~ V_i, ~ n_i) \]

左辺の変数に含まれる体積 \(V\) は混合気体の体積を表しており \(V = V(T, ~ P; ~ \boldsymbol{n})\) とすれば良いので次の様になります。

\[ U\big(T; ~ V(T, ~ P; ~ \boldsymbol{n}), ~ \boldsymbol{n}\big) \equiv U(T, ~ P; ~ \boldsymbol{n}) \]

続いて、式(30)右辺の変数に含まれる \(V_i\) について。

これは混合前の成分 \(i\) の体積を表し、外からは圧力 \(P\) が加えられているので、\(V_i\) は次のように記述できることが分かります。

\[ V_i = V_i(T, ~ P; ~ n_i) \]

したがって式(30)右辺は

\[ \sum_{i = 1}^r U_i\big(T; ~ V_i(T, ~ P; ~ n_i), ~ n_i\big) \equiv \sum_{i = 1}^r U_i(T, ~ P; ~ n_i) \]

となるので、以上から式(42)を得ることができます。

\[ U(T, ~ P; ~ \boldsymbol{n}) = \sum_{i = 1}^r U_i(T, ~ P; ~ n_i) \]

エントロピー

多成分系のエントロピーの式(13)を再掲します。

\[ S(T; ~ V, ~ \boldsymbol{n}) = \sum_{i = 1}^r S_i(T; ~ V, ~ n_i) \]

左辺の変数に含まれる \(V\) は混合気体の体積 \(V = V(T, ~ P; ~ \boldsymbol{n})\) を指しているので次のようにできます。

\[ S\big(T; ~ V(T, ~ P; ~ \boldsymbol{n}), ~ \boldsymbol{n}\big) \equiv S(T, ~ P; ~ \boldsymbol{n}) \]

他方、式(13)右辺の変数に含まれる体積 \(V\) は混合状態の体積と等しく、しかし物質量は \(n_i\) という状態です。

このとき成分 \(i\) の圧力は \(P_i\) となります。

実際、混合気体は今理想的に振る舞うと考えているので、次の状態方程式が成立します。

\[ V = V(T, ~ P; ~ \boldsymbol{n}) = \frac{nRT}{P} \]

そして \(\frac{nRT}{P}\) の分母、分子に \(\frac{n_i}{n}\) を掛けて整理すると \(V\left(T, ~ \frac{n_i}{n}P; ~ n_i\right)\) が得られます。

\[ \frac{\textcolor{red}{\frac{n_i}{n}}nRT}{\textcolor{red}{\frac{n_i}{n}}P} = \frac{n_iRT}{\frac{n_i}{n}P} = V\left(T, ~ \frac{n_i}{n}P; ~ n_i\right) \]

ここで \(\frac{n_i}{n}P\) は式(8)から分圧 \(P_i\) を指していることが分かるので

\[ V\left(T, ~ \frac{n_i}{n}P; ~ n_i\right) = V(T, ~ P_i; ~ n_i) = V \]

したがって、式(13)右辺は次のように記述できます。

\[ \sum_{i = 1}^r S_i\big(T; ~ V(T, ~ P_i; ~ n_i), ~ n_i\big) \equiv \sum_{i = 1}^r S_i(T, ~ P_i; ~ n_i) \]

以上から、式(43)が得られることが分かるでしょう。

\[ S(T, ~ P; ~ \boldsymbol{n}) = \sum_{i = 1}^r S_i(T, ~ P_i; ~ n_i) \]

さて、随分と長くなってしまいましたが式(3)、式(42)、式(43)を式(41)に代入して、多成分系のギブス自由エネルギーを各成分の和で表してみましょう。

\[ G(T, ~ P; ~ \boldsymbol{n}) = \sum_{i = 1}^r U_i(T, ~ P; ~ n_i) + P \sum_{i = 1}^r V_i(T, ~ P; ~ n_i) - T \sum_{i = 1}^r S_i(T, ~ P_i; ~ n_i) \\[15pt] = \sum_{i = 1}^r \big\{ U_i(T, ~ P; ~ n_i) + P V_i(T, ~ P; ~ n_i) - T S_i(T, ~ P_i; ~ n_i) \big\} \]

したがって混合自由エネルギー変化の式(40)は

\[ \Delta G_{\text{mix}} = \sum_{i = 1}^r \big\{ U_i(T, ~ P; ~ n_i) + P V_i(T, ~ P; ~ n_i) - T S_i(T, ~ P_i; ~ n_i) \big\} - \sum_{i = 1}^r G_i(T, ~ P; ~ n_i) \]

また、成分 \(i\) のギブス自由エネルギーも定義から

\[ G_i(T, ~ P; ~ n_i) = U_i(T, ~ P; ~ n_i) + P V_i(T, ~ P; ~ n_i) - T S_i(T, ~ P; ~ n_i) \]

であるから、式(52)に代入して式を整理していくと次式が得られます。

\[ \Delta G_\text{mix} = T \sum_{i = 1}^r \big\{ S_i(T, ~ \textcolor{red}{P}; ~ n_i) - S_i(T, ~ \textcolor{red}{P_i}; ~ n_i) \big\} \]

式(54)右辺に現れるエントロピー差は、成分 \(i\) の圧力の違いによるもので、積分を用いて次のように書き換えることができます。

\[ S_i(T, ~ P; ~ n_i) - S_i(T, ~ P_i; ~ n_i) = \int_{P_i}^P \left( \frac{\partial S}{\partial P} \right)_{T, ~ n_i} dP \]

ここで次のマクスウェルの関係式利用します。

\[ \left( \frac{\partial S}{\partial P} \right)_{T, ~ n_i} = -\left( \frac{\partial V}{\partial T} \right)_{P, ~ n_i} \]

式(56)に理想気体の状態方程式を適用すると

\[ \left( \frac{\partial V}{\partial T} \right)_{P, ~ n_i} = \left( \frac{\partial}{\partial T} ~ \frac{n_iRT}{P}\right)_{P, ~ n_i} = \frac{n_iR}{P} \]

となるので、式(55)の計算を簡単にすることができます。

\[ \begin{align*} S_i(T, ~ P; ~ n_i) - S_i(T, ~ P_i; ~ n_i) &= - \int_{P_i}^P \frac{n_iR}{P} dP \\[15pt] &= n_i R \ln \frac{P_i}{P} \end{align*} \]

したがって、式(58)を式(54)に戻して理想気体における混合自由エネルギー変化の具体的な表式を得ることができます。

\[ \Delta G_\text{mix} = RT \sum_{i = 1}^r n_i \ln \frac{P_i}{P} < 0 \]

繰り返しになりますが、理想気体の混合は自発的に生じます。

ギブス自由エネルギーの計算結果からもその変化量は負となり、温度・圧力一定条件下での混合も自発的に進行することが分かります。