熱力学的な系に対してある状態から別の状態に変化させるとき、その変化が可能であるか否かという予測を実験する前から立てられると非常に便利です。

ここではエントロピーという物理量を定義し、系が起こし得る状態の変化について重要なエントロピー増大の法則を導いていきます。

エントロピー

エントロピーとは

まず始めにエントロピーとは何かを示しておきましょう。

エントロピーとは熱力学系において観測される不可逆な現象を定量的に扱うことを可能にする物理量です。

記号は一般的に \(S\) が利用され、\([\text{J/K}]\) の次元を持ちます。

そしてエントロピーは状態量であり、系の操作前後における平衡状態 \((T; ~ V, ~ n)\) によってその値が決定されます。ただし後ほど説明しますが、状態量として扱えるための条件が存在するので注意しなければなりません。

不可逆性の定量化によるメリット

熱力学現象に見られる不可逆性を定量化できると何が嬉しいのでしょうか。

それは系の状態が別の状態に変化するとき、それが起こり得るのかを事前に知れることです。

最も分かりやすい化学反応を例に説明しましょう。

次に示すのは、水素と酸素から水が生成される反応です。

\[ 2\text{H}_2 + \text{O}_2 ~ \rightarrow ~ 2\text{H}_2\text{O} \]

この反応は反応物の燃焼によって簡単に生じさせることができます。

一方で、生成物である水から元の反応物である水素と酸素への分解は通常起こり得ません。

その理由をエントロピーによって定量的に説明することができるのです。

しかし当ページでは、化学反応がエントロピーによって説明できるところまで踏み込むことはしません。

そもそも熱力学が化学反応系に対して適用できるのか否かも考えていく必要があるでしょう。

他にも身の回りで起きている不可逆な事例はいくつかあります。

例えば気体の自由膨張が挙げられます。

これを実験的に観測するには、図のような仕切りで区切られた容器の片方に気体を満たしておいて、仕切りを取り除く操作を行えば良いです。

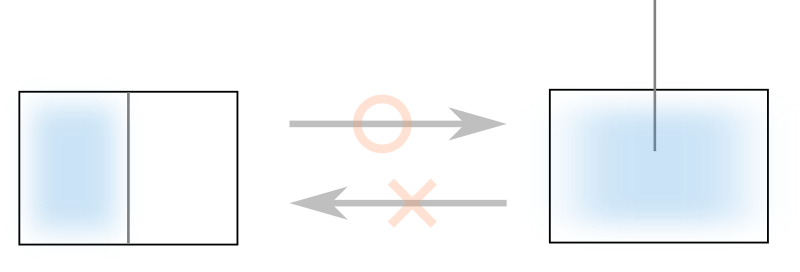
もう片方の領域は真空になっており、この仕切りを取り除くことによって気体はもともと真空だった領域へと流れ込んでいきます。

では逆に、容器全体に気体が満たされた状態から仕切りを挿入することによって、元の状態に戻すことは可能でしょうか。

経験的にも不可能であることは知っての通りですよね。

上記で紹介したことは私達が経験としてどこかで学んできたことです。

しかし今後は未知の対象を取り扱っていかなければならないことも多々あります。

エントロピーを導入することによってその現象が起こり得るのか、あるいは意図的に起こすことができるのかを事前に知ることができるのは非常に大きなメリットです。

では実際に注目している現象を定量的に扱うにはどうすれば良いでしょうか。

具体的な方法を説明する前に、まずは肝心なエントロピーの数学的定義をしていく必要があります。

状態量としてのエントロピー

さて前節までの内容を軽くおさらいしておくと、熱力学系に見られる不可逆な現象を説明する物理量を導入したいという流れでした。

そこで系がある状態から別の状態へ変化するときに、その過程がそもそも可逆なのか不可逆なのかを知る方法が無いかを考えます。

その目的を満たしてくれそうな関係式として、すでに次式に示すクラウジウスの不等式を私達は知っています。

\[ \sum_{i = 1}^N \frac{Q_i}{T_i} \leq 0 ~~~ \text{or} ~~~ \oint \frac{\delta Q}{T} \leq 0 \]

式(2)中の熱は状態量ではないことを明示するために、微小量を \(dQ\) ではなく \(\delta Q\) としていることに注意して下さい。

このクラウジウスの不等式は系を操作して最終的に元の状態に戻すような過程 ( 熱サイクル ) が可逆か不可逆かを定量的に記述することができます。

目標は不可逆な現象を定量的に取り扱えるようになることですが、それは後ほどにして、この節では簡単のために可逆過程のみを考えてみましょう。

熱サイクルが可逆であればクラウジウスの不等式について等号成立が言えるので、次の関係を考えれば良いことになります。

\[ \sum_{i = 1}^N \frac{Q_i}{T_i} = 0 ~~~ \text{or} ~~~ \oint \frac{\delta Q}{T} = 0 ~~~ ( ~ \text{reversible process} ~ ) \]

ここで式(3)を見て気づいてほしいことがあって…

それは \(\frac{Q}{T}\) が状態量であるための条件式となっていることです。

例えば内部エネルギー \(U\) やヘルムホルツ自由エネルギー \(F\) も同様の関係を満たし状態量として扱うことができるのでした。

\[ \begin{align*} \sum_{i = 1}^N \Delta U_i = 0 ~~~ \text{or} ~~~ \oint dU = 0 \\[15pt] \sum_{i = 1}^N \Delta F_i = 0 ~~~ \text{or} ~~~ \oint dF = 0 \end{align*} \]

式(3)と式(4)と比較しながら、新しい状態量であるエントロピー \(S\) を次のように定義します。

\[ \Delta S = \frac{Q}{T} ~~~ \text{or} ~~~ dS = \frac{\delta Q}{T} ~~~ ( ~ \text{reversible process} ~ ) \]

正確にはエントロピーの定義ではなくエントロピー変化の定義となっています。

また状態量ではない熱を温度で割れば状態量になる点もエントロピーの驚くべき特徴です。

エントロピーの温度依存性・体積依存性

ここでは熱現象にエントロピーを適用する際に役立つ関係式を導きます。

• エントロピーの温度依存性
• エントロピーの体積依存性

これらの依存関係は、エントロピーが状態量であることを利用すれば簡単に導くことが可能です。

エントロピー変化の定義式(5)について、熱力学第一法則 \(dU = -\delta W + \delta Q\) を利用して熱 \(\delta Q\) を次のように置き換えてみましょう。

\[ dS = \frac{\delta Q}{T} = \frac{1}{T} (dU + \delta W) \]

前述の通り、熱は状態量ではないので \(\delta Q\) として表記していますが、同様に仕事も状態量ではないため \(dW\) ではなく \(\delta W\) としています。

更に式変形を行っていきます。

微小仕事 \(\delta W\) は系内の圧力と系の体積変化の積 \(P dV\) に置き換えることができます。

内部エネルギー変化 \(dU\) は内部エネルギーが状態量であることを利用して全微分可能性を利用しましょう。

\[ dU = \left(\frac{\partial U}{\partial T}\right)_V dT + \left(\frac{\partial U}{\partial V}\right)_T dV \]

上記の内容にしたがって式(6)を書き換えたものが次式になります。

\[ dS = \frac{1}{T} \left(\frac{\partial U}{\partial T}\right)_V dT + \frac{1}{T} \left\{ \left(\frac{\partial U}{\partial V}\right)_T + P \right\} dV \]

そしてエントロピーが状態量であることから、エントロピーの全微分が

\[ dS = \left(\frac{\partial S}{\partial T}\right)_V dT + \left(\frac{\partial S}{\partial V}\right)_T dV \]

で表されることを利用して \(dT\) および \(dV\) に掛かる係数を比較すれば、次式の関係式が得られます。

\[ \left(\frac{\partial S}{\partial T}\right)_V = \frac{1}{T} \left(\frac{\partial U}{\partial T}\right)_V \]

\[ \left(\frac{\partial S}{\partial V}\right)_T = \frac{1}{T} \left\{ \left(\frac{\partial U}{\partial V}\right)_T + P \right\} \]

エントロピーは実態が理解しづらく取り扱いも非常に困難ではありますが、

上記で導いた関係式によってエントロピーは測定が行いやすい物理量で表現できるようになります。

それではこれらの関係式を実際に利用して、可逆的な熱現象におけるエントロピー変化を計算してみましょう。

エントロピー変化の計算例

エントロピーの温度依存性と体積依存性の関係から、系の状態が変化したときのエントロピー変化を計算できます。

エントロピーは圧力や体積、温度などと同様に状態を記述する状態量ではありますが、直接測定することは普通行わず計算で求めることが基本です。

以下では

• 気体の温度が変化する場合
• 気体の体積が変化する場合
• 気体の温度と体積が変化する場合

についてエントロピー変化を計算してみましょう。

ただし、簡単のために理想気体について考えることにします。

気体の温度変化によるエントロピー変化

気体の温度が変化した場合のエントロピー変化を計算してみましょう。

温度のみが変化し、体積は一定の条件を考えたいのでエントロピーの温度依存性の式(10)を利用します。

式(10)に含まれる \(\frac{\partial U}{\partial T}\) は定積熱容量 \(C_V\) であったことを思い出しましょう。

\[ \left(\frac{\partial U}{\partial T}\right)_V = C_V \]

式(10)を書き換えたものが次式です。

\[ \left(\frac{\partial S}{\partial T}\right)_V = \frac{C_V}{T} \]

いま理想気体を扱っているため、定積熱容量は定数となります。

このことに注意して、系の温度を \(T_\text{A}\) から \(T_\text{B}\) に変化させたときのエントロピー変化を計算します。

それには、式(12)の両辺に \(dT\) を掛けて積分すれば良いので

\[ \begin{align*} \int_{T_\text{A}}^{T_\text{B}} \left(\frac{\partial S}{\partial T}\right)_V dT &= \int_{T_\text{A}}^{T_\text{B}} \frac{C_V}{T} dT \\[15pt] \int_{S(T_\text{A}; ~ V, ~ n)}^{S({T_\text{B}}; ~ V, ~ n)} dS &= C_V \int_{T_\text{A}}^{T_\text{B}} \frac{dT}{T} \\[15pt] S(T_\text{B}; ~ V, ~ n) - S(T_\text{A}; ~ V, ~ n) &= C_V \ln \frac{T_\text{B}}{T_\text{A}} \\[15pt] \therefore ~ \Delta S &= C_V \ln \frac{T_\text{B}}{T_\text{A}} \end{align*} \]

というように、エントロピー変化を求めることができます。

この結果から、系の温度が上昇して \(T_\text{B} > T_\text{A}\) となった場合、エントロピー変化は \(\Delta S > 0\) すなわち系のエントロピーは増加することが分かります。

いま可逆過程を考えているため系の温度を下げる逆過程も存在して、その場合は系のエントロピーは減少すると言えます。

要するにエントロピーは温度についての増加関数であることが分かるでしょう。

この性質は理想気体に限らず、エントロピーの温度依存性 ( 式(10) ) から作業物体に依らず一般的に成立することを理解できます。

気体の体積変化によるエントロピー変化

気体の体積が変化した場合のエントロピー変化を計算してみましょう。

体積のみが変化し、温度は一定の条件を考えたいのでエントロピーの体積依存性 ( 式(11) ) を利用します。

また式(11)に含まれる \(\frac{\partial U}{\partial V}\) は理想気体に置いては 0 と定めたことを思い出しましょう。

\[ \left(\frac{\partial U}{\partial V}\right)_T = 0 ~~~ ( ~ \text{ideal gas} ~ ) \]

式(11)を書き換えたものが次式です。

\[ \left(\frac{\partial S}{\partial V}\right)_T = \frac{P}{T} = \frac{nR}{V} ~~~ (~ PV = nRT ~) \]

では系の体積を \(V_\text{A}\) から \(V_\text{B}\) に変化させたときのエントロピー変化を計算します。

式(14)の両辺に \(dV\) を掛けて積分すれば良いので

\[ \begin{align*} \int_{V_\text{A}}^{V_\text{B}} \left(\frac{\partial S}{\partial V}\right)_T dV &= \int_{V_\text{A}}^{V_\text{B}} \frac{nR}{V} dV \\[15pt] \int_{S(T; ~ V_\text{A}, ~ n)}^{S(T; ~ V_\text{B}, ~ n)} dS &= nR \int_{V_\text{A}}^{V_\text{B}} \frac{dV}{V} \\[15pt] S(T; ~ V_\text{B}, ~ n) - S(T; ~ V_\text{A}, ~ n) &= nR \ln \frac{V_\text{B}}{V_\text{A}} \\[15pt] \therefore ~ \Delta S &= nR \ln \frac{V_\text{B}}{V_\text{A}} \end{align*} \]

というように、エントロピー変化を求めることができます。

この結果から、系の体積が膨張して \(V_\text{B} > V_\text{A}\) となった場合、エントロピー変化は \(\Delta S > 0\) すなわち系のエントロピーは増加することが分かります。

いま可逆過程を考えているため系の体積を縮小させる逆過程も存在して、その場合は系のエントロピーは減少すると言えます。

要するに理想気体のエントロピーは体積についての増加関数であることが分かるでしょう。

気体の温度と体積の変化によるエントロピー変化

最後に気体の温度と体積の両方が変化する場合のエントロピー変化を計算してみたいのですが、結論から言ってしまうと前に計算した2つの結果の和に等しくなります。

\[ \Delta S = C_V \ln \frac{T_\text{B}}{T_\text{A}} + nR \ln \frac{V_\text{B}}{V_\text{A}} \]

求め方は簡単で、状態A \((T_\text{A}; ~ V_{\text{A}}, ~ n)\) から中間状態 \((T_\text{B}; ~ V_{\text{A}}, ~ n)\) に変化させ、最後に状態B \((T_\text{B}; ~ V_{\text{B}}, ~ n)\) にするだけです。

つまり温度に対して積分を実行し、続けて体積に対して積分を実行すれば良いです。

とは言え、エントロピーの全微分は温度項と体積項で分離されているので、一気に積分を実行してしまえば問題ありません。

\[ dS = \left(\frac{\partial S}{\partial T}\right)_V dT + \left(\frac{\partial S}{\partial V}\right)_T dV \\[25pt] \xrightarrow{\text{integrate}} ~ \int_{S(T_\text{A}; ~ V_{\text{A}}, ~ n)}^{S(T_\text{B}; ~ V_{\text{B}}, ~ n)} dS = \int_{T_{\text{A}}}^{T_{\text{B}}} \left(\frac{\partial S}{\partial T}\right)_V dT + \int_{V_{\text{A}}}^{V_{\text{B}}} \left(\frac{\partial S}{\partial V}\right)_T dV \]

式(17)の各項の計算方法は前述同様なので以降の式展開は控えますが、実際に計算を進めれば式(16)が得られることを確認できます。

また理想気体の熱容量が \(C_V = \alpha nR\) であることを用いれば式(16)は更に変形ができて次のように整理できます。

\[ \Delta S = nR \ln \bigg[ \left( \frac{T_\text{B}}{T_\text{A}} \right)^\alpha \frac{V_\text{B}}{V_\text{A}} \bigg] \]

不可逆過程におけるエントロピー変化

前節までは可逆過程に限定して熱現象をエントロピーの観点から理解することに努めてきました。

しかし一般には可逆的な現象よりも不可逆な現象のほうが多いことが事実です。

そして何よりもエントロピーが効果を発揮するのは、不可逆過程を説明するときといっても過言ではありません。

何度も言うように、エントロピー導入のメリットは不可逆な熱現象を定量化できることであり、そして未知の現象をも事前に予測することができる点なのです。

エントロピーを導入する前まで戻って、クラウジウスの不等式から再度始めます。

今度は熱サイクルが不可逆である場合を考えましょう。すなわち次の関係の成立が言えます。

\[ \oint \frac{\delta Q}{T} < 0 ~~~ ( ~ \text{irreversible process} ~ ) \]

ここで式(5)によってエントロピー変化 \(dS\) が \(\frac{\delta Q}{T}\) であると定義されているからと言って、式(19)に代入することはできません。

式(5)は可逆過程という条件が付いていることに注意する必要があります。

だた不可逆サイクルであっても、その経路を上手く設定することでエントロピーを利用できるようになります。

具体的には不可逆サイクルの一部分を可逆過程に置き換えるという方法です。

次の図を見ていただきましょう。

図中の実線が可逆過程を表した経路、破線が不可逆過程を便宜的に表した経路です。

一部分が可逆過程になっていたとしても、系はそれ以外の過程で不可逆な変化をしてしまうので、全体で見れば不可逆サイクルであることに変わりありません。

そして不可逆過程で経由する経路を \(C_1\)、可逆過程で経由する経路を \(C_2\) とすると、式(19)は次のように各過程の積分として分解ができます。

\[ \oint \frac{\delta Q}{T} = \int_{C_1} \frac{\delta Q}{T} + \int_{C_2} \frac{\delta Q}{T} < 0 \]

厳密な表記ではありませんが、式(20)を次の式(21)のように記述しておくほうが分かりやすいかもしれません。

\[ \int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{irr}}}{T} + \int_{\text{B}}^{\text{A}} \frac{\delta Q_{\text{rev}}}{T} < 0 \]

第一項は \(C_1\) に沿って状態Aから状態Bへ不可逆な変化をたどる過程、第二項は \(C_2\) に沿って状態Bから状態Aに可逆的に戻す過程です。

式中の \(\delta Q_{\text{rev}}\), \(\delta Q_{\text{irr}}\) はそれぞれ可逆過程および不可逆過程で系が吸収する熱量を表しています。

更に可逆過程を表す第二項は積分区間を交換できるので、

\[ \int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{irr}}}{T} < - \int_{\text{B}}^{\text{A}} \frac{\delta Q_{\text{rev}}}{T} = \int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{rev}}}{T} \\[15pt] \therefore ~ \int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{irr}}}{T} < \int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{rev}}}{T} \]

という計算結果を得ることができます。

さて不可逆サイクルの一部を可逆過程に置き換えた理由を思い出すと、可逆過程において定義されたエントロピーを不可逆過程でも利用するためでした。

\[ dS = \frac{\delta Q}{T} ~~~ ( ~ \text{reversible process} ~ ) \]

この式(5)を状態Aから状態Bまで積分したときのエントロピー変化を計算すれば

\[ \Delta S_{\text{A} \rightarrow \text{B}} \equiv S(T_\text{B}; ~ V_{\text{B}}, ~ n) - S(T_\text{A}; ~ V_{\text{A}}, ~ n) = \int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{rev}}}{T} \]

となるので、この式(23)を式(22)に代入することで直ちに次式が得られます。

\[ \int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{irr}}}{T} < \Delta S_{\text{A} \rightarrow \text{B}} \]

こうして不可逆過程における \(\frac{Q}{T}\) の総変化とエントロピーの関係を導くことができました。

エントロピー変化 \(\Delta S_{\text{A} \rightarrow \text{B}}\) は状態Aと状態Bのみで一意に決定される量であり、計算できることは前節で確認したとおりです。

そして式(24)が示すように、始点と終点が同じ変化について不可逆過程の場合、熱量と温度の比 \(\frac{\delta Q}{T}\) の総変化量がエントロピー変化よりも小さくなるというのです。

見方を変えれば、式(24)を満たすとき、状態Aから状態Bへの変化は不可逆であると言えます。

断熱過程におけるエントロピー増大

可逆過程と不可逆過程についてエントロピー変化を考えるときに成立する関係式を導いてきました。

そしてここでは、特にエントロピーが断熱過程において真の効果を発揮する事を説明しようと思います。

まずは前節までの内容をまとめたものを次に示しましょう。

\[ \int_{\text{A}}^{\text{B}} \frac{\delta Q}{T} \leq \Delta S_{\text{A} \rightarrow \text{B}}\\[15pt] \left\{ \begin{align*} ~~~ &\int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{rev}}}{T} = \Delta S_{\text{A} \rightarrow \text{B}} ~~~ ( ~ \text{reversible process} ~ ) \\[15pt] ~~~ &\int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{irr}}}{T} < \Delta S_{\text{A} \rightarrow \text{B}} ~~~ ( ~ \text{irreversible process} ~ ) \end{align*} \right. \]

可逆か不可逆かそれぞれの場合で式中の \(\delta Q\) を \(\delta Q_{\text{rev}}\) もしくは \(\delta Q_{\text{irr}}\) に置き換えていることに注意してください。

これら吸熱量をしっかり区別しておかなければ以降の内容で混乱を招く恐れがあります。

断熱可逆過程

断熱可逆過程を考えましょう。

断熱系に対して準静的に操作をすることで系内部の平衡状態を崩さないように変化を与えます。

いま系は可逆過程を経由するので次式を利用すれば良いです。

\[ \int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{rev}}}{T} = \Delta S_{\text{A} \rightarrow \text{B}} \]

更に断熱過程なので \(\delta Q_{\text{rev}} = 0\) とすれば次式が得られます。

\[ \begin{align*} \Delta S_{\text{A} \rightarrow \text{B}} &= 0 \\[15pt] \therefore ~ S(T_\text{A}; ~ V_{\text{A}}, ~ n) &= S(T_\text{B}; ~ V_{\text{B}}, ~ n) \end{align*} \]

つまり状態Aから状態Bへの操作前後で、系のエントロピーは変化しない事を意味しています。

断熱不可逆過程

一方で断熱不可逆過程ではどうでしょうか。

今度は、系は不可逆過程を経由するので次の関係が利用できます。

\[ \int_{\text{A}}^{\text{B}} \frac{\delta Q_{\text{irr}}}{T} < \Delta S_{\text{A} \rightarrow \text{B}} \]

そして断熱過程なので \(\delta Q_{\text{irr}} = 0\) とすれば直ちに次式が得られます。

\[ \begin{align*} \Delta S_{\text{A} \rightarrow \text{B}} &> 0 \\[15pt] \therefore ~ S(T_\text{A}; ~ V_{\text{A}}, ~ n) &< S(T_\text{B}; ~ V_{\text{B}}, ~ n) \end{align*} \]

式(27)が示すように、状態Bにおけるエントロピーは状態Aにおけるエントロピーよりも大きいという結果が得られました。

では上記で示してきたこれら関係が表している内容とは一体どのようなものでしょうか。

エントロピー増大の法則

前項の計算で得られた結果を再度まとめてみましょう。

\[ \Delta S_{\text{A} \rightarrow \text{B}} \geq 0 \\[15pt] \left\{ \begin{align*} ~~~ &\Delta S_{\text{A} \rightarrow \text{B}} = 0 ~~~ ( ~ \text{reversible process} ~ ) \\[15pt] ~~~ &\Delta S_{\text{A} \rightarrow \text{B}} > 0 ~~~ ( ~ \text{irreversible process} ~ ) \end{align*} \right. \]

表現を変えると

\[ S(T_\text{A}; ~ V_{\text{A}}, ~ n) \leq S(T_\text{B}; ~ V_{\text{B}}, ~ n) ~~~ ( ~ \text{A} \rightarrow \text{B} ~ ) \\[15pt] \left\{ \begin{align*} ~~~ S(T_\text{A}; ~ V_{\text{A}}, ~ n) &= S(T_\text{B}; ~ V_{\text{B}}, ~ n) ~~~ ( ~ \text{reversible process} ~ ) \\[15pt] ~~~ S(T_\text{A}; ~ V_{\text{A}}, ~ n) &< S(T_\text{B}; ~ V_{\text{B}}, ~ n) ~~~ ( ~ \text{irreversible process} ~ ) \end{align*} \right. \]

式(29)は系が状態Aから状態Bに変化できるための条件となっています。

つまり断熱過程で系が別の状態に変化するとき、エントロピーは必ず操作前以上になってしまうということです。

逆に言えば、式(29)を満たすような変化でなければ起こり得ないとも考えられます。

この条件を利用すれば、未知の熱現象に対してその変化が起こり得るのか否かを事前に予測することができるのです。

これをエントロピー増大の法則と言います。

断熱自由膨張

エントロピー増大の法則を利用して冒頭で取り上げた気体の自由膨張を理論的に解釈してみましょう。

ここでは理想気体の断熱自由膨張に着目しましょう。

具体的には断熱容器をしきりによって2つに区切り、片方の領域のみに気体を封入します。

仕切りを取り除く操作を行うことで、気体はもう片方の領域へと流れ込んでいきます。

このとき操作前後の系の状態を以下の表のようであったとしましょう。

	操作前	操作後
平衡状態	\((T; ~ V, ~ n)\)	\((T'; ~ V', ~ n)\)

いま断熱不可逆過程を経由して気体は膨張するのでエントロピー増体の法則から次式が成立します。

\[ S(T'; ~ V', ~ n) - S(T; ~ V, ~ n) > 0 \]

またこちらのページで説明していますが、断熱自由膨張では膨張前後の気体の温度に大きな変化は認められません。

それを理想化して理想気体では温度変化が 0 だと扱います。つまり \(T = T'\) ということです。

\[ S(T; ~ V', ~ n) - S(T; ~ V, ~ n) > 0 \]

式(31)を見ると、エントロピー変化を生じさせているのは状態変化前後の体積のみです。

これは前に計算で求めた体積変化におけるエントロピー変化 ( 式(15) ) を利用することができます。

\[ nR \ln \frac{V'}{V} > 0 \]

式(32)は \(V < V'\) の関係を満たしており、系のエントロピー増大によって気体の自由膨張が生じていることが理解できるでしょう。

まとめ

熱力学系で観測される不可逆な現象を定量的に扱うことができるエントロピー \(S\) を導入しました。

エントロピーは数学的に次式で表現されます。

\[ \Delta S = \frac{Q}{T} ~~~ \text{or} ~~~ dS = \frac{\delta Q}{T} \]

ここで \(Q\) は系が環境から吸収する熱量、\(T\) は環境の温度です。

注意すべきなのは、上記の関係は可逆過程で定義されている事です。

ただ不可逆過程においても次のエントロピー増大の法則を利用することで熱現象を定量的に扱うことができます。

\[ S(T_{\text{A}}; ~ V_{\text{A}}, ~ n) \leq S(T_{\text{B}}; ~ V_{\text{B}}, ~ n) \]

この不等式は断熱系が状態A \((T_{\text{A}}; ~ V_{\text{A}}, ~ n)\) から状態B \((T_{\text{B}}; ~ V_{\text{B}}, ~ n)\) に変化する際に成立する関係です。

つまり熱力学系は状態が変化するにあたって、断熱系のエントロピーが操作前の状態以上にしかならない事を指しています。

このエントロピー増大の法則を利用すれば、未知の熱現象に対してその変化が起こり得るのか、意図的に起こすことができるのかを事前に予測することができるようになります。