物体の熱容量について詳しく解説していきます。

また最後には「仕事」と「熱」が熱力学的に等しいことも見ていきます。

熱容量とは

熱容量とは、系の温度を 1 \([\text{K}]\) 変化させるのに必要なエネルギー変化のことを言います。

特に体積一定条件における熱容量を定積熱容量 \(C_V\) と言って、系の温度変化 \(\Delta T\) および内部エネルギー変化 \(\Delta U\) を用いて次のように書けます。

\[ C_V \equiv \lim_{\Delta T \rightarrow 0} \frac{\Delta U}{\Delta T} = \left( \frac{\partial U}{\partial T} \right)_{V, ~ n} \]

内部エネルギーは温度についての増加関数であり、その偏微分係数は常に 0 以上の値を持つため、同様に定積熱容量も 0 以上となります。

熱容量と仕事

内部エネルギー変化が断熱仕事に等しいことを利用して、定積熱容量を仕事で表すことができます。

断熱系の内部エネルギーが \(\Delta U\) だけ変化するとき、系は外界に断熱仕事 \(W_\text{ad}\) をし、それらの関係は次式のとおりになるのでした。

\[ \Delta U = -W_\text{ad} \]

したがって定積熱容量は次のように表すことができるでしょう。

\[ C_V = - \frac{W_\text{ad}}{\Delta T} \]

しかしより簡便であるのは、外から系に加える仕事 \(W_\text{ex}\) を用いて表すことです。

一般に「系が外界にする仕事」と「外から系に加える仕事」は完全に一致しませんが、静かに操作することでほとんど一緒とみなすことができるでしょう。

そこで \(W_\text{ex} \simeq - W_\text{ad}\) とすれば式(3)は次式に書き換えることができます。

\[ C_V \simeq \frac{W_\text{ex}}{\Delta T} \]

こうすることで熱容量は系の温度を 1 \([\text{K}]\) 上昇させるのに必要な仕事量とも解釈できます。

仕事量の計算は容易なので、式(4)を用いて系の熱容量を決定することが可能になります。

熱容量の測定 : ジュールの実験

ここでは「水」を例に、熱容量の測定方法を紹介します。

次の図に示すような水が入った断熱容器に対し、撹拌翼を用いて仕事することを考えましょう。

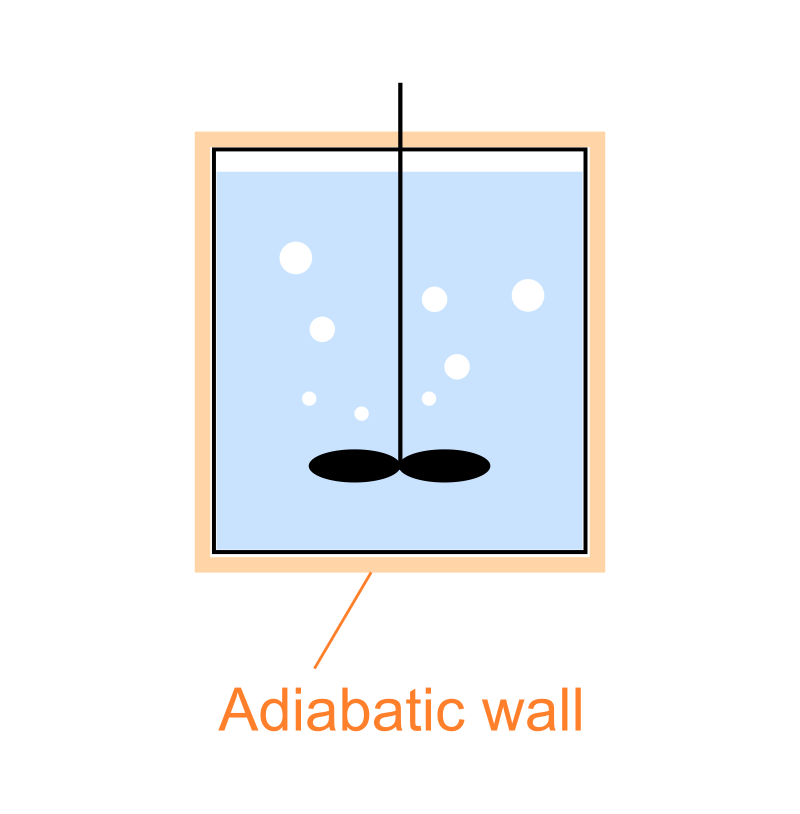
これは「ジュールの実験」と呼ばれる実験を簡略化したものになります。

外から加える仕事量を変化させることで、撹拌翼の回転量を制御します。

このとき撹拌翼を落下する物体と繋げてその位置エネルギーの変化量を仕事に充てたり、また一般的には装置を用いて電気的に制御する方法が取られます。

そして同実験において重要なことは、前後で体積を変化させない断熱操作であることです。

\[ (T; ~ V, ~ n) ~ \xrightarrow{\text{a}} ~ (T'; ~ V, ~ n) \]

容器の内部で撹拌翼を動かすだけなので、系の体積は変化しません。

この断熱操作(1)では操作後の温度が操作前の温度よりも高くなる ( \(T < T'\) ) という事実があります。

つまり撹拌翼による仕事量に応じて、断熱容器内の水の温度は上昇するのです。

次に示すのは、3000 \([\text{g}]\) の水に対して仕事 \(W_\text{ex} ~ [\text{J}]\) を与えたときに、系の温度 \(t ~ [{}^\text{o}\text{C}]\) が上昇する様子を表したグラフです。

定積熱容量 \(C_V\) は式(4)を用いてグラフの傾きから求められ、実際に水の場合はおよそ 12500 \([\text{J/K}]\) と見積もることができます。

また実際に用いた水の質量で割ることによって、比熱 \(c ~ [\text{J/g･K}]\) を得ることができ、水の場合は

\[ c = \frac{12500}{3000} \simeq 4.17 ~ [\text{J/g･K}] \]

と求まります。

熱容量の物質依存性

前節では水の熱容量について取り上げましたが、熱容量は物質によって様々な値を持ちます。

実際に歴史的に見ると熱容量は次のように定義されました。

\[ \frac{C_2}{C_1} = \frac{t - t_1}{t_2 - t} \]

これは温度の異なる2つの物体を接触させたときに生じる温度変化の比を表しています。

温度 \(t_1\)、\(t_2\) にあった物体1、物体2は共に温度 \(t\) に収束します。

また式(5)をよく見ると、熱容量と温度変化の関係は逆比の関係になっており、要するに熱容量が大きいほど温度変化は小さく、逆に熱容量が小さければ温度変化が大きいことになります。

• 熱量量 : 大 → 温度変化 : 小
• 熱量量 : 小 → 温度変化 : 大

また熱容量は温度依存性もあり、次のように温度で展開されて用いられます。

\[ C_V = a_0 + a_1 T + a_2 T^2 + \cdots \]

温度 \(T^k\) の係数 \(a_k\) は物質ごとに異なる値を取ります。

しかし前節の水の例からも分かるように、狭い温度範囲においてはほとんど温度依存性はなく熱容量は定数とみなせます。

状況に応じて温度依存性を考慮する必要があるか否かを判断する必要があるでしょう。

理想気体の熱容量

熱力学では分子の存在を仮定しなくても成立する理論体系です。

しかし、分子という粒子の運動をベースに組み立てられる気体分子運動論によって、理想気体の熱容量を理論的に導くことができます。

詳細は別のページに譲りますが、結果だけを示すと次のとおりです。

\[ C_V = \alpha nR \]

\(\alpha\) は気体の種類によって異なる値を取り、単原子分子であれば \(\alpha = \frac{3}{2}\)、二原子分子では \(\alpha = \frac{5}{2}\) となることが分かっています。

また理想気体の熱容量は温度に依存しないことも特徴です。

熱容量と熱

熱容量は「熱」という語が含まれるように、熱とも関係があります。

熱 \(Q\) は式(5)を整理した

\[ C_1 (t - t_1) = C_2 (t_2 - t) = Q \]

という表式で定義することをこちらで説明したとおりです。

改めて単一物体について熱と熱容量の関係を記述したものが次式になります。

\[ Q = C \Delta T \]

物体が外部と熱のやり取りを行うことで生じる温度変化を、断熱操作(1)と同様に記述すると次のようになります。

\[ (T; ~ V, ~ n) ~ \rightarrow ~ (T'; ~ V, ~ n) \]

ただし注意すべきは、上記の変化は断熱系ではなく外部と熱のやり取りを行える系であることです。

また操作(2)では物体の体積は変化しない状況を想定しており、このとき式(8)の熱容量 \(C\) は定積熱容量 \(C_V\) と等しくなります。

つまり、定積熱容量 \(C_V\) は次式のように表すこともできる事となり

\[ C_V = \frac{Q}{\Delta T} \]

すなわち定積熱容量とは温度変化に要する熱量であると解釈も可能ということになります。

ここで一旦「熱容量」という名称の意味について触れておこうと思います。

これは「熱」という"物質"が系にどれくらい蓄えられるかという発想で命名されたと考えると分かりやすいでしょうか。

その物質のことを18世紀当時は「熱素」などと呼ばれていたらしいです…。

事実として熱が物質であるという解釈は誤りで、現代的には温度差のある箇所に生じるエネルギーの流れを表すのでした。

ですが、この場限りで当時の解釈を拝借させてもらいます！

すると前節で示した熱容量と物質の温度変化のしやすさについてもイメージが湧きやすいはずです。

• 熱量量 : 大 → 温度変化 : 小
• 熱量量 : 小 → 温度変化 : 大

熱容量が大きいとは、「熱」を蓄えることができるスペース ( 余力、ゆとり…何と言えば伝わる？ ) が大きいという事です。

物質にはこの仮想的なスペースをいくつも有していると考えられます。

そしてこのスペースに熱を溜めていき満タンになったら 1 \([{}^\text{o}\text{C}]\) 上昇する、そして溢れた熱はまた別のスペースに溜めていくという構図です。

つまり熱容量というスペースが大きいと 1 \([{}^\text{o}\text{C}]\) 上昇するまでにより多くの熱を要するということです。

逆に熱容量が小さければ温度変化しやすいことも理解できるでしょう。

仕事と熱の等価性

ここまで「熱容量」を趣旨として話を展開してきましたが、注目したいのは熱容量 \(C_V\) が内部エネルギー \(\Delta U\) 、仕事 \(W_\text{ad}\) 、熱 \(Q\) を用いて表現できたことです。

この事実から「仕事」と「熱」の間にある関係を見出していこうと思います。

結論としては「仕事」と「熱」は熱力学的に等価であると言うことができて、これは系の内部エネルギー変化が「仕事」によるものか「熱」によるものかについて考えていくと分かってくる内容です。

前節までに扱ってきた系の操作を以下に示しますが…

\[ (T; ~ V, ~ n) ~ \xrightarrow{\text{a}} ~ (T'; ~ V, ~ n) \]

\[ (T; ~ V, ~ n) ~ \rightarrow ~ (T'; ~ V, ~ n) \]

この通り操作方法は異なりますが操作前後の系の状態は両方同じです。

これら2つの操作における内部エネルギー変化を考えたとき、状態量の性質から両方とも同じ変化量であることが分かります。

つまり操作(1)で生じる内部エネルギー変化は仕事と等しく、操作(2)では熱と等しいと言うことができます。

\[ \begin{align*} \text{Ope.(1) : }&\Delta U = U(T', ~ V, ~ n) - U(T, ~ V, ~ n) = - W_\text{ad}\big( (T, ~ V, ~ n) \rightarrow (T', ~ V, ~ n) \big) \\[15pt] \text{Ope.(2) : }&\Delta U = U(T', ~ V, ~ n) - U(T, ~ V, ~ n) = Q \end{align*} \]

繰り返しになりますが、内部エネルギー変化は同じでありながら、その変化の原因は仕事と熱で異なる場合があることが分かります。

しかし最初 \((T; ~ V, ~ n)\) の状態にあった系が \((T'; ~ V, ~ n)\) に変化していたとして、その原因は何かと問われると、仕事あるいは熱のどちらによるものかを明らかにすることはできません。

ここから逆に考えると「仕事」と「熱」は系の状態変化の要因として一見異なるものではあるものの、熱力学においては本質的に等価であると言えるわけです。