系がある状態から別の状態に変化できるかどうかは、ギブス自由エネルギーという熱力学量から判断することができます。

当ページではギブス自由エネルギーとは何か、そしてどの様に導かれるのかについてわかりやすく解説します。

ギブス自由エネルギー

等温・定圧条件にある熱力学系が初期状態から別の状態に変化可能かを判定する便利な熱力学量があります。

ギブス自由エネルギー \(G\) と言って、その変化量 \(\Delta G\) は次式で表されます。

\[ \begin{align*} \Delta G &= \Delta U + P \Delta V - T \Delta S \\[15pt] ( ~ dG &= dU + P dV - T dS~ ) \end{align*} \]

ここで \(\Delta U\) は系の内部エネルギー変化、\(P\) は系に加えられた圧力、\(\Delta V\) は系の体積変化、\(T\) は外部環境の温度、\(\Delta S\) は系のエントロピー変化を表します。

後で分かりますがこのギブス自由エネルギー変化が \(\Delta G \leq 0\) となるとき系の状態変化が許されます。

ところで系がある状態から別の状態に変化することはエントロピー増大の法則によって判定ができました。

しかし同法則が効果を発揮するのは断熱条件であることが前提です。

上記ギブス自由エネルギーを利用することによって、断熱条件でなくとも系がどのように変化するかを知ることができるのです。

ギブス自由エネルギーの導出

ギブス自由エネルギー変化の式と状態変化の進行について、エントロピー増大の法則から導くことができます。

それは熱力学第一法則を導出する際に紹介した等温極限をエントロピー増大の法則について考えることで得られます。

次に示すような中央の容器を断熱された容器で覆った複合系を考えて…

外側の容器の大きさを無限に取ることでほぼ等温環境としてみなせる状況を考えるわけです。

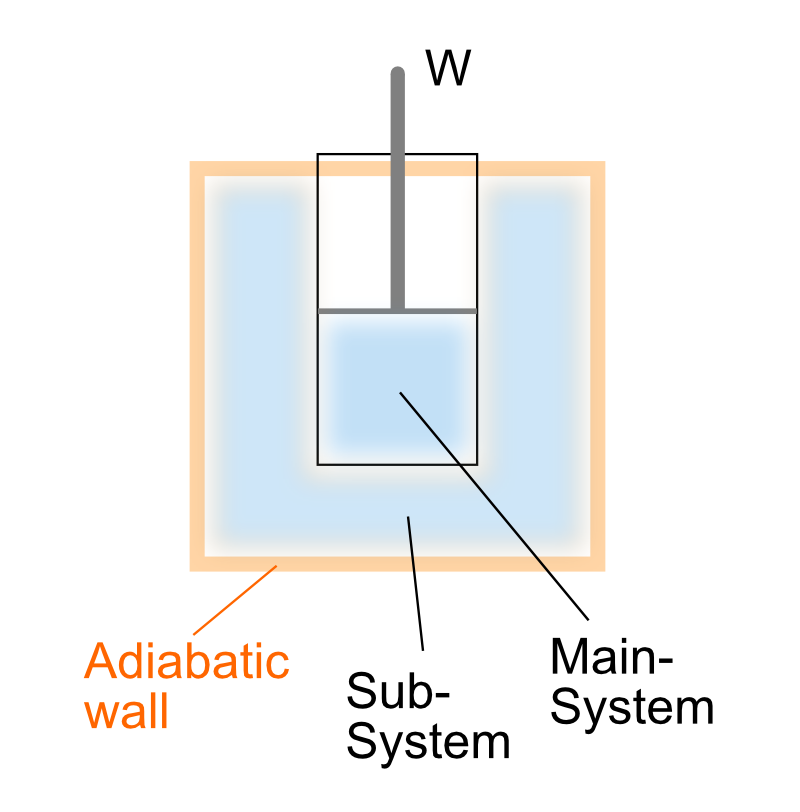
また簡単のために中央の容器が体積変化するとき仕事は断熱壁よりも更に外側にするように設計をします。

つまり中央の容器が仕事をする際、外側の容器の体積変化は生じないということです。

ここから複合系に対してエントロピー増大の法則を適用していきます。

最終的に着目したいのは中央の容器で起こる変化ですが、エントロピー増大の法則を適用するために断熱複合系"全体"について考える必要があります。

このとき、中央の容器と外側の容器の体積および物質量の組を考えると便利でそれぞれ \(\boldsymbol{V} = (V, ~ V_\text{sub})\)、\(\boldsymbol{n} = (n, ~ n_\text{sub})\) のように表すことにします。

複合断熱系全体が状態A \((T_\text{A}; ~ \boldsymbol{V}_\text{A}, ~ \boldsymbol{n}_\text{A})\) から状態B \((T_\text{B}; ~ \boldsymbol{V}_\text{B}, ~ \boldsymbol{n}_\text{B})\) に変化するとき、すなわち

\[ (T_\text{A}; ~ \boldsymbol{V}_\text{A}, ~ \boldsymbol{n}_\text{A}) ~ \xrightarrow{\text{a}} ~ (T_\text{B}; ~ \boldsymbol{V}_\text{B}, ~ \boldsymbol{n}_\text{B}) \]

という断熱過程をたどるとき、エントロピー増大の法則から次の不等式が成立します。

\[ S(T_\text{A}; ~ \boldsymbol{V}_\text{A}, ~ \boldsymbol{n}_\text{A}) \leq S(T_\text{B}; ~ \boldsymbol{V}_\text{B}, ~ \boldsymbol{n}_\text{B}) \]

操作前後におけるそれぞれの容器の状態は次のようになっていたとしましょう。

	操作前	操作後
中央の容器	\((T_\text{A}; ~ V_\text{A}, ~ n_\text{A})\)	\((T_\text{B}; ~ V_\text{B}, ~ n_\text{B})\)
外側の容器	\((T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub})\)	\((T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub})\)

すると、エントロピーの相加性から複合系全体のエントロピーは中央の容器と外側の容器のエントロピーに分解ができます。

\[ \begin{align*} S(T_\text{A}; ~ \boldsymbol{V}_\text{A}, ~ \boldsymbol{n}_\text{A}) = S(T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) + S(T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub}) \\[15pt] S(T_\text{B}; ~ \boldsymbol{V}_\text{B}, ~ \boldsymbol{n}_\text{B}) = S(T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) + S(T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub}) \end{align*} \]

式(3)を式(2)に代入することで次式が得られます。

\[ S(T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) + S(T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub}) \leq S(T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) + S(T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub}) \]

次に外側の容器の状態変化のみに着目します。

\[ (T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub}) ~ \rightarrow ~ (T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub}) \]

このときエントロピー変化は次のように記述できます。

\[ \int_{(T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub})}^{(T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub})} \frac{\delta Q}{T} \leq S(T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub}) - S(T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub}) \]

ここで等温極限を考えましょう。外側の容器の大きさを無限にするのでした ( \(V_\text{sub} \rightarrow \infty, ~ n_\text{sub} \rightarrow \infty\) )。

具体的な計算は割愛しますが、重要なのはこの数学的操作によって \(T_\text{B} \rightarrow T_\text{A}\) となることです。

つまり外側の容器は等温環境とみなすことができ、改めてその温度を \(T_\text{A} = T_\text{B} \equiv T\) と表すことにすると、式(5)は

\[ \frac{Q_\text{sub}}{T} \leq \lim_{\substack{{V_\text{sub} \rightarrow \infty}\\[2pt]{n_\text{sub} \rightarrow \infty}}} S(T_\text{B}; ~ V_\text{sub}, ~ n_\text{sub}) - S(T_\text{A}; ~ V_\text{sub}, ~ n_\text{sub}) \]

となることが分かります。

\(Q_\text{sub}\) は外側の容器が中央の容器から吸収した熱量を表しています。

そして、式(4)と式(6)から次の不等式が成立することも分かります。

\[ - \frac{Q_\text{sub}}{T} \leq S(\textcolor{red}{T}; ~ V_\text{B}, ~ n_\text{B}) - S(\textcolor{red}{T}; ~ V_\text{A}, ~ n_\text{A}) \]

中央の容器の温度も外側と同様に温度が \(T\) に置き換わることに注意して下さい。

最後に \(Q_\text{sub}\) を中央の容器が吸収する熱量 \(Q\) で置き換えます。

それには \(Q + Q_\text{sub} = 0\) という関係が成立していることを利用すれば良いだけです。

\[ \frac{Q}{T} \leq S(T; ~ V_\text{B}, ~ n_\text{B}) - S(T; ~ V_\text{A}, ~ n_\text{A}) \]

以上で等温条件において成立するエントロピー法則 ( 式(8) ) の導出は完了となります。

※…と長々と説明をしてきましたが、実はこの関係はエントロピー変化の定義式 \(\Delta S \geq \int \frac{\delta Q}{T}\) を単に温度一定として積分記号を外したものと同じになります。

ギブス自由エネルギーによる第二法則

では、ここからギブス自由エネルギーの導入までを見てきましょう。

式(8)について、熱 \(Q\) を熱力学第一法則 \(\Delta U = -W + Q\) を利用して内部エネルギーと仕事に置き換えます。

そして式を整理したものが次になります。

\[ \Delta U + W \leq T \Delta S ~~~ ( ~ \Delta S \equiv S(T; ~ V_\text{B}, ~ n_\text{B}) - S(T; ~ V_\text{A}, ~ n_\text{A}) ~ ) \]

外から系に一定の圧力 \(P_\text{ex}\) が加わっているとき、系がする仕事 \(W\) は \(P_\text{ex} \Delta V\) で表すことができるので

\[ \Delta U + P_\text{ex} \Delta V - T \Delta S \leq 0 \]

となって、式(10)左辺は冒頭で示したギブス自由エネルギー変化 ( 式(1) ) と同じことが分かります！

式(1)と比較して式(10)では圧力が外から加えられたものになっていますが、等号成立する準静的過程においては系の圧力と等しくなるので一般性を考えて \(P\) を用いることにしましょう。

したがって、等温・定圧条件において系が状態変化するために満たすべき関係式は次式となります。

\[ \Delta G \leq 0 \\[15pt] \left\{ \begin{align*} ~ \Delta G &= 0 ~~~ ( ~ \text{reversible process} ~ )\\[15pt] ~ \Delta G &< 0 ~~~ ( ~ \text{irreversible process} ~ ) \end{align*} \right. \]

また以上の内容からギブス自由エネルギーは次のように記述できると定めます。

\[ G = U + PV - TS \]

実際に式(12)の全微分を考えて、等温・定圧条件 \( ( ~ dT = 0, ~ dP = 0 ~ ) \) を設けることで式(1)が導けることを確認できます。

\[ \begin{align*} dG &= dU + d(PV) - d(TS) \\[15pt] &= dU + (V dP + P dV) - (S dT + T dS) \\[15pt] &= dU + P dV - T dS ~~~ ( ~ dP = 0, ~ dT = 0 ~ ) \end{align*} \]

ヘルムホルツ自由エネルギーによる第二法則

また式(10)に体積一定の条件を加えたとき、系の状態変化はヘルムホルツ自由エネルギーによって判定ができるようになります。

実際 \(\Delta V = 0\) とすると式(10)は

\[ \Delta U - T \Delta S \leq 0 \]

となりますが、いま等温条件下にあることから左辺はヘルムホルツ自由エネルギーに置き換えることができるので結果として次式が得られます。

\[ \Delta F \leq 0 \\[15pt] \left\{ \begin{align*} ~ \Delta F &= 0 ~~~ ( ~ \text{reversible process} ~ )\\[15pt] ~ \Delta F &< 0 ~~~ ( ~ \text{irreversible process} ~ ) \end{align*} \right. \]

式変形で利用した \(\Delta F = \Delta U - T \Delta S\) の関係が成立することは以下のページで解説しています。

ギブス自由エネルギーの性質

ギブス自由エネルギーが満たす性質を紹介します。

列挙すると次の3つです。

• 相加性
• 示量性

以上は式(12)から分かって、ギブス自由エネルギーを構成する熱力学量 \(U\)、\(V\)、\(S\) が上記を満たすのと同様です。

加えてギブス自由エネルギーが状態量であることも問題ないでしょう。

上記2つの性質について、以下で簡単に解説していきます。

相加性

ギブス自由エネルギーは相加性を満たします。

異なる単一系を複合させたとき、全体のギブス自由エネルギーは単一系におけるそれの総和に等しくなります。

例えば、2つの単一系におけるギブス自由エネルギーが \(G_1(T_1; ~ V_1, ~ n_1)\)、\(G_2(T_2; ~ V_2, ~ n_2)\) であったとき複合系は

\[ G_1(T_1; ~ V_1, ~ n_1) + G_2(T_2; ~ V_2, ~ n_2) \]

のギブス自由エネルギーを持つということです。

示量性

ギブス自由エネルギーは示量性を満たします。

つまり系の大きさを \(\lambda\) 倍したとき、エネルギーも同様に \(\lambda\) 倍になります。

\[ \begin{align*} G(T; ~ \lambda V, ~ \lambda n) &= U(T; ~ \lambda V, ~ \lambda n) + P ~ \lambda V - TS(T; ~ \lambda V, ~ \lambda n) \\[15pt] &= \lambda U(T; ~ V, ~ n) + \lambda PV - \lambda TS(T; ~ V, ~ n) \\[15pt] &= \lambda \{U(T; ~ V, ~ n) + PV - TS(T; ~ V, ~ n)\} \\[15pt] &= \lambda G(T; ~ V, ~ n) \end{align*} \]

ギブス自由エネルギーの制御変数

前節ではギブス自由エネルギーの変数を温度 \(T\)、体積 \(V\)、物質量 \(n\) として \(G(T; ~ V, ~ n)\) のように扱いましたが、実はギブス自由エネルギーではこれら以外のより自然な変数の組が存在します。

結論から言えば温度 \(T\)、圧力 \(P\)、物質量 \(n\) の組であり、\(G(T, ~ P; ~ n)\) と記述します。

これはギブス自由エネルギーを等温・定圧の条件下におけるエネルギーとして導入したことからも言えるのですが、系のギブス自由エネルギーを制御するには外部環境の温度か系に加える圧力を様々変化させるようになるためです。

このような変数のことを制御変数と呼ぶことにします。

次にギブス自由エネルギーの制御変数が温度と圧力になることを数学的に示します。

制御変数を動かしたときにギブス自由エネルギーがどのくらい変化するかを知るには、ギブス自由エネルギーの全微分を考えると良いです。

\[ dG = dU + V dP + P dV - S dT - T dS \]

しかしながら式(17)の右辺には微分が5つもあり、ギブス自由エネルギーを変化させる要因は余りにも複雑です。

ここから熱力学第一法則を利用して内部エネルギー変化 \(dU\) を消去すれば微分は \(dP\) と \(dT\) の2つに整理することができるのです。

実際に熱力学第一法則について

\[ dU = -\delta W + \delta Q \]

微小仕事 \(\delta W\) は \(PdV\) で、微小吸熱量 \(\delta Q\) は \(TdS\) で置き換えることができ

\[ dU = -PdV + TdS \]

続けて、式(19)を式(17)に代入すれば

\[ \begin{align*} dG &= (-PdV + TdS) + V dP + P dV - S dT - T dS \\[15pt] \therefore ~ dG&= VdP - SdT \end{align*} \]

が得られます。

こうしてギブス自由エネルギー変化を温度変化と圧力変化によって表すことができました。

ところで、ギブス自由エネルギーの全微分は次のように書くこともできます。

\[ dG = \left( \frac{\partial G}{\partial P} \right)_{T, ~ n} dP + \left( \frac{\partial G}{\partial T} \right)_{P, ~ n} dT \]

さて式(21)から何が分かるかを次節で示していきます。

ギブス自由エネルギーの圧力依存性

式(20)と式(21)を比較することによって、ギブス自由エネルギーの圧力依存性を導けます。

\[ \begin{align*} \text{eq(20) : } & dG = VdP - SdT \\[15pt] \text{eq(21) : } & dG = \left( \frac{\partial G}{\partial P} \right)_{T, ~ n} dP + \left( \frac{\partial G}{\partial T} \right)_{P, ~ n} dT \end{align*} \]

圧力変化 \(dP\) の係数を比較すれば次式を導くことができます。

\[ \left( \frac{\partial G}{\partial P} \right)_{T, ~ n} = V \]

理想気体の圧力依存性

理想気体についてギブス自由エネルギーの圧力依存性を考えてみましょう。

理想気体の状態方程式 \(V = \frac{nRT}{P}\) を式(22)に代入し、温度および物質量一定の条件で次のように積分をします。

\[ \begin{align*} \left( \frac{\partial G}{\partial P} \right)_{T, ~ n} &= \frac{nRT}{P} \\[15pt] \int_{P_\text{A}}^{P_\text{B}} \left( \frac{\partial G}{\partial P} \right)_{T, ~ n} dP &= \int_{P_\text{A}}^{P_\text{B}} \frac{nRT}{P} dP \end{align*} \]

上式を整理したものが下記になります。

\[ G(T, ~ P_\text{B}; ~ n) - G(T, ~ P_\text{A}; ~ n) = nRT \ln \frac{P_\text{B}}{P_\text{A}} \]

式(23)は状態 \((T, ~ P_\text{A}; ~ n)\) にある系を圧力操作によって状態 \((T, ~ P_\text{B}; ~ n)\) に変化させたときのギブス自由エネルギー変化を表します。

また一般に圧力操作前の状態は、標準状態 ( \(10^5 ~ [\text{Pa}], ~ 25 ~ [^\text{o}\text{C}]\) ) を選択します。

このときの圧力を \(P^\circ ~ ( ~ = 10^5 ~ )\) と表すことにして、任意の圧力 \(P\) における理想気体の自由エネルギーを

\[ G(T, ~ P; ~ n) = G(T, ~ P^\circ; ~ n) + nRT \ln \frac{P}{P^\circ} \]

と表すことにします。

もしくはギブス自由エネルギーの変数が具体的に示されていない場合は

\[ G = G^\circ + nRT \ln \frac{P}{P^\circ} \]

と表されることも多いです。

ギブス自由エネルギーの温度依存性

前節で示した圧力依存性と同様に、ギブス自由エネルギーの温度依存性も式(20)と式(21)の比較から直ちに導くことができます。

\[ \left( \frac{\partial G}{\partial T} \right)_{P, ~ n} = -S \]

理想気体の温度依存性

理想気体のギブス自由エネルギーはどのような温度依存性をもつのかを確認してみましょう。

理想気体のエントロピーは次で与えられます。

\[ \begin{align*} S(T; ~ V, ~ n) &= S(T_0; ~ V_0, ~ n) + nR\ln \bigg[ \left( \frac{T}{T_0} \right)^\alpha \frac{V}{V_0} \bigg] \\[15pt] &= S(T_0; ~ n \bar{V}_0, ~ n) + nR\ln \bigg[ \left( \frac{T}{T_0} \right)^\alpha \frac{V}{n \bar{V}_0} \bigg] ~~~ \left( ~ \bar{V}_0 = \frac{V_0}{n} ~ \right) \end{align*} \]

\((T; ~ V, ~ n)\) は任意の状態、\((T_0; ~ V_0, ~ n)\) は初期状態を表します。

式中の \(\alpha\) は気体の種類に依存する定数です。また、エントロピーの示量性を担保するために初期状態のモル体積 \(\bar{V}_0 = \frac{V_0}{n}\) を用いました。

式(26)を式(25)に代入してみましょう。

\[ \left( \frac{\partial G}{\partial T} \right)_{P, ~ n} = - S(T_0; ~ n \bar{V}_0, ~ n) - nR\ln \bigg[ \left( \frac{T}{T_0} \right)^\alpha \frac{V}{n \bar{V}_0} \bigg] \]

さて式(27)を両辺温度で積分するのですが、この計算は少し長いのでここでは結果のみを示します ( 詳しい計算方法はこちらをどうぞ )。

\[ G(T, ~ P^\circ; ~ n) = nRT - nRT\ln \left(\frac{T}{T_0}\right)^{\alpha + 1} + U(T, ~ P^\circ; ~ n) - TS(T_0, ~ P^\circ; ~ n) \]

ただし \(P^\circ\) は標準圧力であり、状態方程式 \(P^\circ V(T_0, ~ P^\circ; ~ n) = nRT_0\) を満たすものとします。

また前節の内容と合わせて考えると、すなわち圧力変化と温度変化があるとき任意の状態 \((T, ~ P; ~ n)\) におけるギブス自由エネルギー \(G(T, ~ P; ~ n)\) は

\[ G(T, ~ P; ~ n) = nRT - nRT \ln \bigg[ \left( \frac{T}{T_0} \right)^{\alpha + 1} \frac{P^\circ}{P} \bigg] + U(T, ~ P^\circ; ~ n) - TS(T_0, ~ P^\circ; ~ n) \]

で与えられることになります。