大正準集団 ( グランドカノニカルアンサンブル ) とは、温度、化学ポテンシャル、体積 \((T, ~ \mu; ~ V)\) が一定の系を要素とした集団です。

これらの要素間では熱のやり取りと物質のやり取りが可能です。

つまり大正準集団の概念を理解することによって、開放系に関する統計力学の知見を得ることができます。

大正準集団 ( グランドカノニカルアンサンブル )

大正準集団 ( グランドカノニカルアンサンブル ) は、温度、化学ポテンシャル、体積 \((T, ~ \mu; ~ V)\) が一定の系を要素にもつ集団です。

それぞれの要素は互いに熱のやり取りと物質のやり取りを行うことができます。

そもそも、このような系を要素とした集団を考えるのは、系の平均的な状態を計算するのに役に立つためです。

例えば集団を構成する要素を ある1つの系の経時変化つまりスナップ写真と捉えることによって、集団の平均を考えたときに系の時間平均を計算した事と同じになります。

そして時間平均によって求められた物理量は、実は熱力学的な測定量を指すことになります。

ここで統計力学的アプローチによって熱力学現象をミクロの立場から理解することが可能になるという流れです。

大正準分布 ( グランドカノニカル分布 )

大正準集団全体でみたとき、それぞれの要素はエネルギーの揺らぎが生じています。

異なるエネルギーを持つ要素がどのくらいの比率で存在するかを表したものを大正準分布 ( グランドカノニカル分布 )と呼びます。

以降では大正準分布を導く過程を丁寧に解説していきます。

大正準分布 ( グランドカノニカル分布 ) の導出

大正準集団の要素は互いに熱と物質のやり取りが可能であり、それに伴って要素が取り得るエネルギーも2つの要因によって決められます。

そこで要素が取り得るエネルギーを \(E_{i,N} ~ \big( 0 \leq i \leq r, ~ 0 \leq N \leq s \big)\)、また \(E_{i,N}\) のエネルギーを持つ要素の数を \(M_{i,N}\) と記述することにします。

\(E_{i,N}\) についてもう少し…これは \(i\) 番目のエネルギー準位について、更に分子が \(N\) 個の場合に分けて考えたエネルギーを表しています。

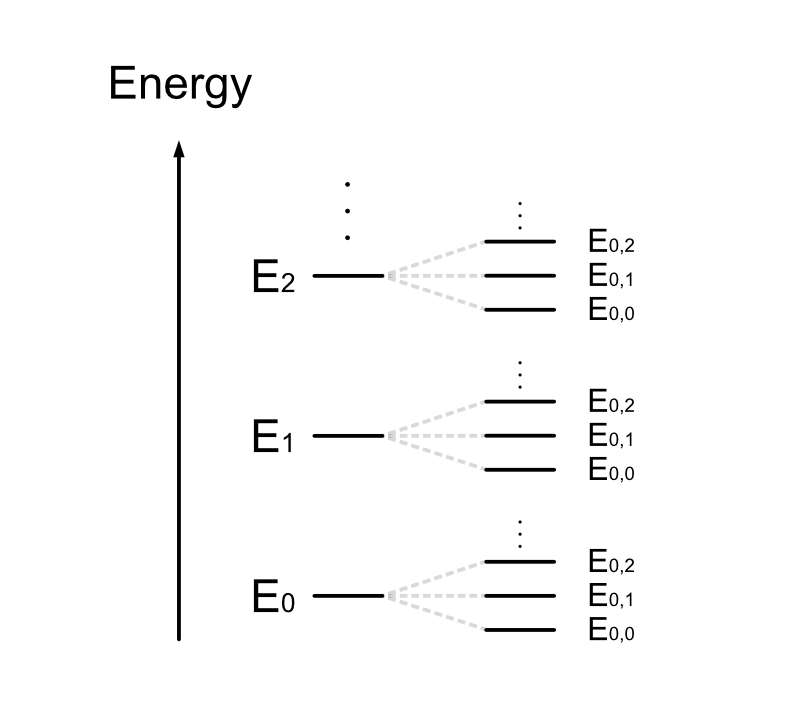
一見複雑に思えますが、考えるエネルギー準位の数が多いだけです。

ではエネルギー \(E_{0,0}\), \(E_{1,0}\), \(E_{2,0}\) \(\cdots\) \(E_{i,N}\) \(\cdots\) \(E_{r,s}\) を持つ要素の数が \(M_{0,0}\), \(M_{1,0}\), \(M_{2,0}\) \(\cdots\) \(M_{i,N}\) \(\cdots\) \(M_{r,s}\) であるときの状態数 \(W\) を求めましょう。

\(i\) および \(N\) の両方を変化させたときに考え得るすべての状態を考慮するので、つまり状態数 \(W\) は

\[ W = \frac{M!}{M_{0,0}! M_{1,0}! M_{2,0}! \cdots M_{i,N}! \cdots M_{r,s}!} = \frac{M!}{\prod_{i = 0}^r \prod_{N = 0}^s M_{i,N}!} \]

のように記述できます。

簡単のために各エネルギー準位の縮退度は1としました。

状態数 \(W\) は対数表示にすると扱いやすい表式に整理することができます。

\[ \ln W = \ln M! - \ln \prod_{i = 0}^r \prod_{N = 0}^s M_{i,N}! \\[15pt] = \ln M! - \sum_{i = 0}^r \sum_{N = 0}^s \ln M_{i,N}! \]

ここでスターリングの公式 \(\ln M! \simeq M \ln M - M\) を用いて更に式変形を行うと次式が得られます。

\[ \ln W = M \ln M - M - \sum_{i = 0}^r \sum_{N = 0}^s \big( M_{i,N} \ln M_{i,N} - M_{i,N} \big) \\[15pt] = M \ln M - \sum_{i = 0}^r \sum_{N = 0}^s M_{i,N} \ln M_{i,N} \]

集団全体として最も起こり得る状態は、状態数 \(W\) が最大値を場合と考えられ、そのときの要素数の組 \(M_{0,0}\), \(M_{1,0}\), \(M_{2,0}\) \(\cdots\) \(M_{i,N}\) \(\cdots\) \(M_{r,s}\) を求める必要があります。

最大最小問題を解くためには、微分法を利用すればよく \(\ln W\) を \(M_{j,L}\) で微分すると

\[ \frac{\partial \ln W}{\partial M_{j,L}} = - \sum_{i = 0}^r \sum_{N = 0}^s \left( \frac{\partial M_{i,N}}{\partial M_{j,L}} \ln M_{i,N} + M_{i,N} \frac{\partial \ln M_{i,N}}{\partial M_{j,L}} \right) \\[15pt] = - \sum_{i = 0}^r \sum_{N = 0}^s \left( \frac{\partial M_{i,N}}{\partial M_{j,L}} \ln M_{i,N} + \frac{\partial M_{i,N}}{\partial M_{j,L}} \right) \\[15pt] = - \sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} \ln M_{i,N} \]

が得られます。

\(W\) を最大化するにあたり、各エネルギー準位の要素数 \(M_{0,0}\), \(M_{1,0}\), \(M_{2,0}\) \(\cdots\) \(M_{i,N}\) \(\cdots\) \(M_{r,s}\) を変化させて極値を探すというのが式(4)の示す内容ですが、実際は要素数を任意に変化させることは不可能であり次の条件を満たす必要があります。

\[ \begin{align*} &\sum_{i = 0}^r \sum_{N = 0}^s M_{i,N} = M ~~~ ( ~ \text{Const.} ~ ) \\[15pt] &\sum_{i = 0}^r \sum_{N = 0}^s M_{i,N} E_{i,N} = E_\text{ens} ~~~ ( ~ \text{Const.} ~ ) \\[15pt] &\sum_{i = 0}^r \sum_{N = 0}^s M_{i,N} N = N_\text{ens} ~~~ ( ~ \text{Const.} ~ ) \end{align*} \]

つまり集団全体で要素の総数 \(M\) は変化しないことや、それぞれの要素 ( 系 ) を構成する分子の総数 \(N_\text{ens}\) は変化しないという事です。

また条件として集合全体の総エネルギー \(E_\text{ens}\) は一定であることも加えます。

上記条件の下で \(\ln W\) を最大化する要素数を求める必要があります。

拘束条件付きの最大最小問題は、ラジュランジュ未定係数法を利用するのが良く、計算に際して拘束条件式(5)を両辺 \(M_{j,L}\) で偏微分した

\[ \begin{align*} &\sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} = 0 \\[15pt] &\sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} E_{i,N} = 0 \\[15pt] &\sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} N = 0 \end{align*} \]

が必要になります。

実際にラグランジュ未定係数法を適用すると

\[ \begin{align*} \text{eq(7.1) : } ~~~ & \frac{\partial \ln W}{\partial M_{j,L}} = \alpha \sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} + \beta \sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} E_{i,N} + \gamma \sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} N \\[25pt] \Leftrightarrow ~~~ & - \sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} \ln M_{i,N} = \alpha \sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} + \beta \sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} E_{i,N} + \gamma \sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} N \\[30pt] \text{eq(7.2) : } ~~~ & \therefore ~ \sum_{i = 0}^r \sum_{N = 0}^s \frac{\partial M_{i,N}}{\partial M_{j,L}} \big( \ln M_{i,N} + \alpha + \beta E_{i,N} + \gamma N \big) = 0 \end{align*} \]

ここで式(7)に現れる \(\alpha\), \(\beta\), \(\gamma\) はそれぞれ未定係数です。

式(7.2)において \(\frac{\partial M_{i,N}}{\partial M_{j,L}} ~ \char`≠ ~ 0\) であるから

\[ \ln M_{i,N} = -\alpha - \beta E_{i,N} - \gamma N \]

の関係を満たす必要があります。

\(M_{i,N}\) について解くと

\[ M_{i,N} = e^{-\alpha - \beta E_{i,N} - \gamma N} \]

となって、異なるエネルギー状態をもつ要素の数 \(M_{j,L}\) との比から大正準分布を得ることができます。

\[ \frac{M_{i,N}}{M_{j,L}} = e^{-\beta (E_{i,N} - E_{j,L}) - \gamma (N - L)} \]

大正準集団の要素の期待値

大正準集団の要素の間ではエネルギーと分子のやり取りが行われています。

前述の通り集団を考えて統計的な取り扱いを行うのは、そこから熱力学的性質と比較してミクロとマクロの現象を繋げることでした。

測定によって得られる熱力学量は系の時間的な平均として理解され、それには物理量の期待値を考えることが重要です。

期待値を求める前提として確率分布 \(\frac{M_{i,N}}{M}\) を計算しておくと、式(10)から

\[ \begin{align*} \text{eq(10) : } ~~~ \frac{M_{i,N}}{M_{j,L}} &= e^{-\beta (E_{i,N} - E_{j,L}) - \gamma (N - L)} \\[15pt] \Leftrightarrow ~~ M_{j,L} &= M_{i,N} e^{\beta (E_{i,N} - E_{j,L}) + \gamma (N - L)} \\[25pt] \xrightarrow{ ~~~ \sum ~~~ } ~~ \sum_{j = 0}^r \sum_{L = 0}^s M_{j,L} &= \sum_{j = 0}^r \sum_{L = 0}^s M_{i,N} e^{\beta (E_{i,N} - E_{j,L}) + \gamma (N - L)} \\[15pt] M &= M_{i,N} e^{\beta E_{i,N} + \gamma N} \sum_{j = 0}^r \sum_{L = 0}^s e^{-\beta E_{j,L} - \gamma L} \\[25pt] \therefore ~ \frac{M_{i,N}}{M} &= \frac{e^{-\beta E_{i,N} - \gamma N}}{\displaystyle \sum_{j = 0}^r \sum_{L = 0}^s e^{-\beta E_{j,L} - \gamma L}} \end{align*} \]

となります。

ここで可読性に配慮して、次の \(\Xi\) を定義します。

\[ \Xi \equiv \sum_{j = 0}^r \sum_{L = 0}^s e^{-\beta E_{j,L} - \gamma L} \]

すると確率分布式(11)は次のようになります。

\[ \frac{M_{i,N}}{M} = \frac{e^{-\beta E_{i,N} - \gamma N}}{\Xi} \]

確率分布式(13)を利用して、大正準集団の要素が平均的にどのくらいのエネルギーまた分子数を持つのかを求めてみましょう。

エネルギー期待値

エネルギー期待値 \(\bar{E}\) は次の計算に従って得ることができます。

\[ \begin{align*} \bar{E} &= \sum_{i = 0}^r \sum_{N = 0}^s E_{i,N} \frac{M_{i,N}}{M} \\[15pt] &= \frac{1}{\Xi} \sum_{i = 0}^r \sum_{N = 0}^s E_{i,N} e^{-\beta E_{i,N} - \gamma N} \end{align*} \]

更に式(14)の和の部分は \(\Xi\) を用いて次のように書くこともできます。

\[ \begin{align*} \sum_{i = 0}^r \sum_{N = 0}^s E_{i,N} e^{-\beta E_{i,N} - \gamma N} &= - \frac{\partial}{\partial \beta} \sum_{i = 0}^r \sum_{N = 0}^s e^{-\beta E_{i,N} - \gamma N} \\[15pt] &= - \frac{\partial \Xi}{\partial \beta} \end{align*} \]

したがって、エネルギー期待値の式(14)は次のように書き換えられることが分かります。

\[ \bar{E} = -\frac{1}{\Xi} \frac{\partial \Xi}{\partial \beta} = - \frac{\partial \ln \Xi}{\partial \beta} \]

繰り返しになりますが、エネルギー期待値は熱力学的に測定される系のエネルギーを表します。

分かりやすく言うと、エネルギー期待値 \(\bar{E}\) は系の内部エネルギー \(U\) に等しいということです。

分子数の期待値

続いて分子数の期待値 \(\bar{N}\) は次の計算によって得られます。

\[ \begin{align*} \bar{N} &= \sum_{i = 0}^r \sum_{N = 0}^s N \frac{M_{i,N}}{M} \\[15pt] &= \frac{1}{\Xi} \sum_{i = 0}^r \sum_{N = 0}^s N e^{-\beta E_{i,N} - \gamma N} \end{align*} \]

式(17)の和の部分は \(\Xi\) を用いて

\[ \begin{align*} \sum_{i = 0}^r \sum_{N = 0}^s N e^{-\beta E_{i,N} - \gamma N} &= -\frac{\partial}{\partial \gamma} \sum_{i = 0}^r \sum_{N = 0}^s e^{-\beta E_{i,N} - \gamma N} \\[15pt] &= -\frac{\partial \Xi}{\partial \gamma} \end{align*} \]

と表すことができるので、式(18)を式(17)に戻して整理すると分子数の期待値は次式になります。

\[ \bar{N} = - \frac{1}{\Xi} \frac{\partial \Xi}{\partial \gamma} = - \frac{\partial \ln \Xi}{\partial \gamma} \]

大正準分布の未定係数の決定

最後に未定係数 \(\beta\), \(\gamma\) を決定します。

大正準集団の要素の状態数について記述した式(3)を次のように書き直して

\[ \begin{align*} \text{eq(3) : } ~~~~~ \ln W &= M \ln M - \sum_{i = 0}^r \sum_{N = 0}^s M_{i,N} \ln M_{i,N} \\[15pt] &= - \sum_{i = 0}^r \sum_{N = 0}^s M_{i,N} \ln \frac{M_{i,N}}{M} \end{align*} \]

ここに確率分布式(13) \(\frac{M_{i,N}}{M}\) を代入して計算を進めていきます。

\[ \begin{align*} \ln W &= - \sum_{i = 0}^r \sum_{N = 0}^s M_{i,N} \ln \frac{e^{-\beta E_{i,N} - \gamma N}}{\Xi} \\[15pt] &= \sum_{i = 0}^r \sum_{N = 0}^s \big( \beta M_{i,N} E_{i,N} + \gamma M_{i,N} N + M_{i,N} \ln \Xi\big) \\[20pt] &= \beta M \bar{E} + \gamma M \bar{N} + M \ln \Xi \end{align*} \]

等号の最後では期待値の式(14)および式(17)を利用しました。

ここで、大正準集団の要素について平均的な微視的状態が \(w\) である場合…

このとき集団の状態数 \(W\) は次のように記述することができます。

\[ W = w^M \]

そして式(22)を式(21)に代入して整理すると次式が得られます。

\[ \ln w = \beta \bar{E} + \gamma \bar{N} + \ln \Xi \]

更にボルツマンの原理からエントロピーと微視的状態の関係 \(S = k_\text{B} \ln w\) を用いると式(23)は

\[ S = k_\text{B} \left( \beta \bar{E} + \gamma \bar{N} + \ln \Xi \right) \]

となります。

エントロピーの全微分を計算すると

\[ dS = k_\text{B} \left( \bar{E} d\beta + \beta d\bar{E} + \bar{N} d\gamma + \gamma d\bar{N} + d\ln \Xi \right) \]

また式(25)に現れる全微分 \(d\ln \Xi\) について、式(16)および式(19)の結果から次式が得られるので

\[ \begin{align*} d\ln \Xi &= \left( \frac{\partial \ln \Xi}{\partial \beta} \right)_\gamma d\beta + \left( \frac{\partial \ln \Xi}{\partial \gamma} \right)_\beta d\gamma \\[15pt] &= -\bar{E} d\beta - \bar{N} d\gamma \end{align*} \]

式(26)から式(25)は次のようになります。

\[ dS = k_\text{B} \left( \beta d\bar{E} + \gamma d\bar{N} \right) \]

全微分の定義から \(dS\) は

\[ dS = \left( \frac{\partial S}{\partial \bar{E}} \right)_{\bar{N}} d\bar{E} + \left( \frac{\partial S}{\partial \bar{N}} \right)_{\bar{E}} d\bar{N} \]

であるため、式(27)と比較すると次の関係式が得られます。

\[ \begin{align*} \left( \frac{\partial S}{\partial \bar{E}} \right)_{\bar{N}} = k_\text{B} \beta \\[15pt] \left( \frac{\partial S}{\partial \bar{N}} \right)_{\bar{E}} = k_\text{B} \gamma \end{align*} \]

エントロピーについて、熱力学によればエネルギーおよび物質量 ( 分子数 ) の偏微分係数はそれぞれ次の関係で与えられます。

\[ \begin{align*} \text{eq(30.1) : } ~~~ & \left( \frac{\partial S}{\partial \bar{E}} \right)_{\bar{N}} = \frac{1}{T} \\[15pt] \text{eq(30.2) : } ~~~ & \left( \frac{\partial S}{\partial \bar{N}} \right)_{\bar{E}} = -\frac{1}{N_\text{A}}\frac{\mu}{T} = -\frac{\^\mu}{T} \end{align*} \]

式(30.2)については物質量ではなく分子数での偏微分を行ったので、右辺ではアボガドロ数 \(N_\text{A}\) で割った分子数あたりの量で表しています。また改めて1分子あたりの化学ポテンシャル \(\^\mu\) を定めます。

したがって式(29)および式(30)から \(\beta\) と \(\gamma\) を決定することができます。

\[ \begin{align*} \beta &= \frac{1}{k_\text{B}T} \\[15pt] \gamma &= - \frac{\^\mu}{k_\text{B}T} \end{align*} \]

以上をまとめると大正準分布も具体的な表式として次式で与えられることが分かります。

\[ \begin{align*} \text{eq(10) : } ~~~ \frac{M_{i,N}}{M_{j,L}} &= e^{-\beta (E_{i,N} - E_{j,L}) - \gamma (N - L)} \\[15pt] &= e^{- \frac{E_{i,N} - E_{j,L}}{k_\text{B}T} + \frac{\^\mu(N - L)}{k_\text{B}T}} \\[20pt] \therefore ~ \frac{M_{i,N}}{M_{j,L}} &= e^{- \frac{(E_{i,N} - E_{j,L}) - \^\mu (N - L)}{k_\text{B}T}} \end{align*} \]