熱力学を学ぶ意義の1つとしてカルノーの定理があります。

熱力学系から仕事を取りだすための具体的な機関としてカルノーサイクルがありますが、取り出せる仕事には上限があり熱効率という量で定義されるのでした。

カルノーの定理を学ぶことによって、熱効率について理解を深めることができます。

しかし同定理の示す内容は至ってシンプルではあるのですが、それを示す過程は非常に数学的であり少しクセがあります。

当ページでは、そのようなカルノーの定理の証明を丁寧に解説することを試みます。

カルノーの定理とは

カルノーの定理とは、カルノーサイクルのように2つの熱源で動作する系について、その最大熱効率は作業物体によらず2つの温度のみで決まるというものです。

• 最大熱効率は作業物体によらない
• 最大熱効率は2つの温度のみで決まる

カルノーサイクルについて解説した際、理想気体を作業物体としたときの系の熱効率 \(\eta\) は次式で表現されることを導きました。

\[ \eta = \frac{W_{\text{cyc}}}{Q_{\text{in}}} = 1 - \frac{T_{\text{low}}}{T_{\text{high}}} \]

\(W_{\text{cyc}}\) は着目している系が熱サイクル1周を経て外界にした仕事、\(Q_{\text{in}}\) は高温熱源から系が吸収した熱を表しており、それらの比が熱効率の定義でした。

そして理想気体の熱効率 式(1) は実際にカルノーの定理による主張どおりに低温熱源の温度 \(T_{\text{low}}\) 、高温熱源の温度 \(T_{\text{high}}\) の2つのみで表現されています。

更に同定理は作業物体に依存することなく熱効率は同じであることも同時に主張していることから、例えば実在気体について考えたとしても熱効率は式(1)で与えられると言うのです。

この定理の証明は極めて数学的かつ巧妙であり筆者自身も理解に苦労しましたが、必要な知識から順を追って説明していくので是非付いてきて下さい。

不可逆サイクルは可逆サイクルよりも熱効率が低い

まずは不可逆サイクルと可逆サイクルの熱効率について理解する事から初めます。

結論から言ってしまえば不可逆サイクルは可逆サイクルと比較して必ず熱効率が小さくなります。

不可逆サイクルの熱効率を \(\eta_{\text{~irr}}\)、可逆サイクルの熱効率を \(\eta_{\text{~rev}}\) として次式が常に成立します。

\[ \eta_{\text{~irr}} < \eta_{\text{~rev}} \]

添字は irreversible ( 不可逆 ) および reversible ( 可逆 ) から来ています。

では、なぜ式(2)の理解が必要になるかを簡単に説明しておきましょう。

それは異なる2つの可逆サイクルを考えたとき、それぞれの熱効率が等しくなることを示すためです。

これからウォーミングアップを行って、必要となる事前知識を拾い集めていく段階にあると思って下さい。

証明の鍵となるのは2つのサイクルの連結

ここから巧妙な内容となっていきます。

式(2)の関係を示すに当たって、不可逆サイクルと可逆サイクルの2つを用意します。

ただしこれらのサイクルは2つの熱源のみで動作可能なものを選択しておくとします。

2つの熱源間で動作する可逆サイクルの代表例はカルノーサイクルですので、以下の内容における「可逆サイクル」とは「カルノーサイクル」だと思っていただいても問題ありません。

そしてこれらのサイクルを熱源間で運転させる際にポイントとなるのが、2つのサイクルを連結させて1つの系として捉える事です。

実際に図で説明したほうが分かりやすいでしょう、以下を御覧ください。

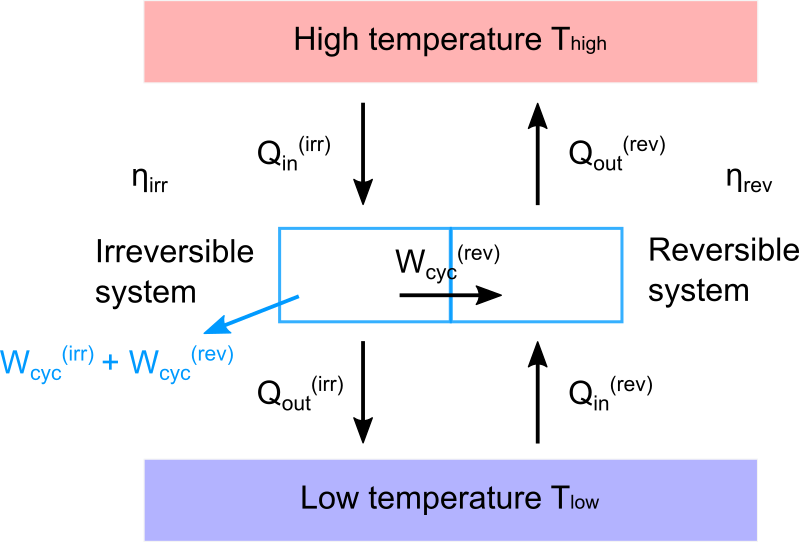
図中の左側には不可逆サイクル、右側には可逆サイクルを置いています。

不可逆サイクルでは高温熱源から熱を吸収して一部を仕事に変換し、残りを熱として低温熱源に逃します。

熱効率 \(\eta_{\text{~irr}}\) は次式で表現できます。

\[ \eta_{\text{~irr}} = \frac{W_{\text{cyc}}^{\text{(irr)}}}{Q_{\text{in}}^{\text{(irr)}}} \]

一方で可逆サイクルは逆方向に運転させます。

この逆サイクルでは順方向に運転させたときとは真逆の動きをするので、

すなわち外からの仕事によって低温熱源から高温熱源への熱移動が実現されるということです。

「低温熱源から高温熱源への熱の移動は可能なのか」と思われるかもしれませんが、外から仕事を行ったという点が重要であり、もちろん経験的に知っての通り何も手を加えなければ自然には起こり得ません。

※余談ですがこの原理を利用したものが冷却器で、冷房の動作の説明などに利用されたりしています。

そしてこの逆サイクルの熱効率は…というと少し違和感を覚えるかもしれませんが…丁寧に考えるとそう難しくはありません。

もともとこの可逆サイクルを順方向に運転させたときには、ある大きさの熱量を高温熱源から吸収するわけですが、

逆方向の操作によって元通りの状態に戻すことができるので、逆操作を行えば同じ大きさの熱量だけを高温熱源に戻すことになります。

要するに順方向で高温熱源から吸収する熱量の絶対値は、図中の \(Q_{\text{out}}^{\text{(rev)}}\) の絶対値と等しいということです。

以上を踏まえると、結局逆方向に運転しているサイクルの熱効率は符号に注意して次式で表現できます。

\[ \eta_{\text{~rev}} = \frac{- W_{\text{cyc}}^{\text{(rev)}}}{- Q_{\text{out}}^{\text{(rev)}}} = \frac{W_{\text{cyc}}^{\text{(rev)}}}{Q_{\text{out}}^{\text{(rev)}}} \]

式(4)中のマイナスは、仕事は系が外界にするときを正に取り、熱は系が外から吸収するときに正に取っていることが理由です。

つまり \(W_{\text{cyc}}^{\text{(rev)}}\) も \(Q_{\text{out}}^{\text{(rev)}}\) も負の値であることに注意して下さい。

結果的にマイナスはキャンセルされ、熱効率は正の値を取ることを確認できます。

ここで熱力学第一法則 \(\Delta U = -W + Q\) を利用して、仕事と熱の関係を導いておきましょう。

いま系の状態を元通りに戻すサイクルを考えているため、状態量である内部エネルギーの変化 \(\Delta U\) は 0 とすることができます。

不可逆サイクルおよび可逆サイクルに対して熱力学第一法則を適用すると以下の関係式が得られます。

\[ \begin{align*} 0 &= - W_{\text{cyc}}^{\text{(irr)}} + Q_{\text{in}}^{\text{(irr)}} + Q_{\text{out}}^{\text{(irr)}} \\[15pt] 0 &= - W_{\text{cyc}}^{\text{(rev)}} + Q_{\text{in}}^{\text{(rev)}} + Q_{\text{out}}^{\text{(rev)}} \end{align*} \]

念の為ですが、仕事と熱の正負を表にしておきました。

	仕事	吸熱	排熱
不可逆サイクル	\(W_{\text{cyc}}^{\text{(irr)}} > 0\)	\(Q_{\text{in}}^{\text{(irr)}} > 0\)	\(Q_{\text{out}}^{\text{(irr)}} < 0\)
可逆サイクル	\(W_{\text{cyc}}^{\text{(rev)}} < 0\)	\(Q_{\text{in}}^{\text{(rev)}} > 0\)	\(Q_{\text{out}}^{\text{(rev)}} < 0\)

※式(5)の不可サイクルから計算される関係式について、「不可逆なので内部エネルギーはもとに戻らないのではないか」と思われるかもしれませんが、等温過程で等温環境と接触させる機会があるので内部の状態は完全に元に戻すことができます。

式(2) \(\eta_{\text{~irr}} < \eta_{\text{~rev}}\) を証明するために、順方向に動作する不可逆サイクルと、逆方向に動作する可逆サイクルを連結して1つの系として見ましたが、

このとき不可逆サイクルがする仕事を、可逆サイクルがすべて受け取るような設計をすることで状況が非常に簡単になります。

どういう事かと言うと、仕事のやり取りが 連結した系内 のみで完結するので、外界とのやり取りが一切ない状況を考えることができるのです。

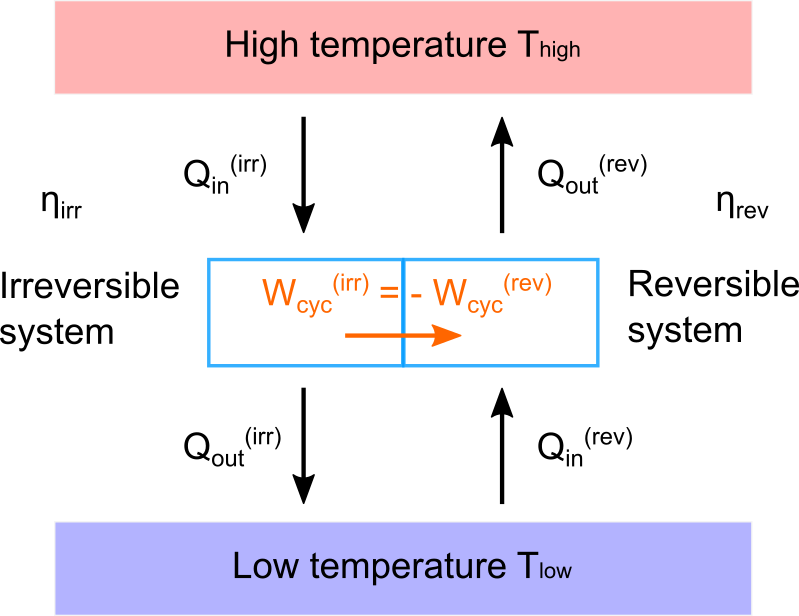
外界との仕事のやり取りがないので、すなわち \(W_{\text{cyc}}^{\text{(irr)}} = - W_{\text{cyc}}^{\text{(rev)}}\) ということですから、熱効率の式(3)および式(4)から直ちに次式が得られます。

\[ \begin{align*} \text{eq : (3)} ~ \eta_{\text{~irr}} = \frac{W_{\text{cyc}}^{\text{(irr)}}}{Q_{\text{in}}^{\text{(irr)}}}&, ~~~ \text{eq : (4)} ~ \eta_{\text{~rev}} = \frac{W_{\text{cyc}}^{\text{(rev)}}}{Q_{\text{out}}^{\text{(rev)}}} \\[30pt] W_{\text{cyc}}^{\text{(irr)}} &= - W_{\text{cyc}}^{\text{(rev)}} \\[15pt] \Leftrightarrow ~ \eta_{\text{~irr}} Q_{\text{in}}^{\text{(irr)}} &= \eta_{\text{~rev}} \left( - Q_{\text{out}}^{\text{(rev)}} \right) \end{align*} \]

加えて熱力学第一法則から得られた関係式(5)から、次式の成立が言えます。

\[ \text{eq(5) : }\left\{ \begin{align*} ~~~ 0 &= - W_{\text{cyc}}^{\text{(irr)}} + Q_{\text{in}}^{\text{(irr)}} + Q_{\text{out}}^{\text{(irr)}} \\[15pt] ~~~ 0 &= - W_{\text{cyc}}^{\text{(rev)}} + Q_{\text{in}}^{\text{(rev)}} + Q_{\text{out}}^{\text{(rev)}} \end{align*} \right. \\[30pt] \begin{align*} & W_{\text{cyc}}^{\text{(irr)}} = - W_{\text{cyc}}^{\text{(rev)}} \\[15pt] \Leftrightarrow ~ & Q_{\text{in}}^{\text{(irr)}} + Q_{\text{out}}^{\text{(irr)}} = - Q_{\text{in}}^{\text{(rev)}} - Q_{\text{out}}^{\text{(rev)}} \end{align*} \]

さて、ここから数学的かつ熱力学の原理に則って、不可逆サイクルが可逆サイクルよりも必ず小さい熱効率 ( 式(2) ) になることを示していきます。

\(\eta_{\text{~irr}} < \eta_{\text{~rev}}\) のとき

「数学的」というのは単に場合分けを行うことです。

この条件のときに物理原則に反さないことを確認できればOKです。

熱効率の大小関係と式(6)を比較することによって次の不等式の関係が得られます。

\[ \begin{align*} & Q_{\text{in}}^{\text{(irr)}} > - Q_{\text{out}}^{\text{(rev)}} \\[15pt] \therefore ~ & Q_{\text{in}}^{\text{(irr)}} + Q_{\text{out}}^{\text{(rev)}} > 0 \end{align*} \]

これに伴って式(6)および式(7)から次の関係も得られます。

\[ \begin{align*} & Q_{\text{in}}^{\text{(rev)}} < -Q_{\text{out}}^{\text{(irr)}} \\[15pt] \therefore ~ & Q_{\text{in}}^{\text{(rev)}} + Q_{\text{out}}^{\text{(irr)}} < 0 \end{align*} \]

では式(8)および式(9)が表す意味は一体どういったことでしょうか。

その答えは、2つのサイクルを連結した系と熱源とがやり取りする正味の熱量を表しています。

次の図を見て下さい。

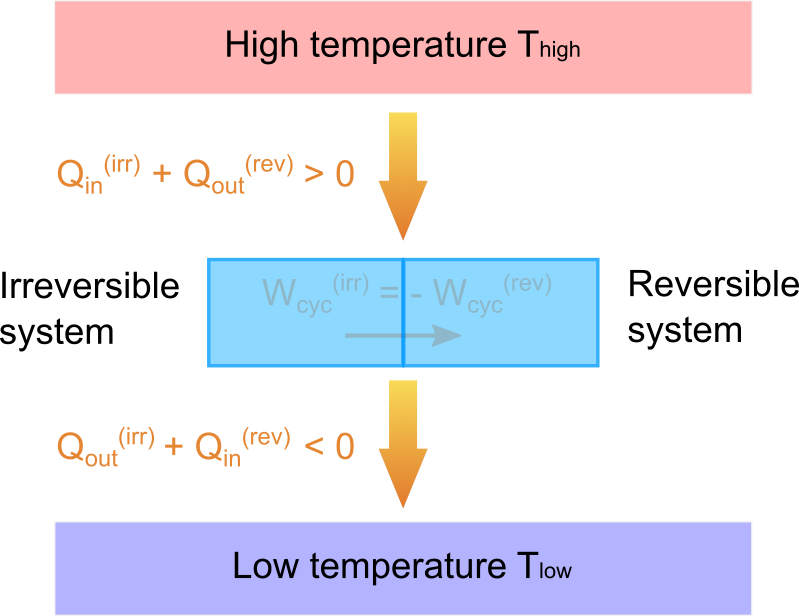
つまり式(8)は2つのサイクルが連結された系と高温熱源がやり取りする熱量を、式(9)は低温熱源とやり取りする熱量を指しています。

そして熱の移動は系が吸収するときに正の値を取るように設定しているので、式(8)と式(9)から連結系は高温熱源から \(Q_{\text{in}}^{\text{(irr)}} + Q_{\text{out}}^{\text{(rev)}}\) だけ熱を吸収し、低温熱源に \(Q_{\text{in}}^{\text{(rev)}} + Q_{\text{out}}^{\text{(irr)}}\) だけ熱を逃がすことが分かります。

このように \(\eta_{\text{~irr}} < \eta_{\text{~rev}}\) のとき、熱は高温熱源から低温熱源に流れるという経験事実に合致する内容を導くことができるのです。

\(\eta_{\text{~irr}} > \eta_{\text{~rev}}\) のとき

逆に不可逆サイクルの熱効率が可逆サイクルの熱効率よりも大きい場合では、経験事実に合わず不都合が生じてしまいます。

議論は先程と全く同様なので一気に示してしまいますが、

まずは熱効率の大小関係と式(6)から次式を得ます。

\[ \begin{align*} & Q_{\text{in}}^{\text{(irr)}} < - Q_{\text{out}}^{\text{(rev)}} \\[15pt] \therefore ~ & Q_{\text{in}}^{\text{(irr)}} + Q_{\text{out}}^{\text{(rev)}} < 0 \end{align*} \]

直ちに式(10)と式(5)から次の関係も得られます。

\[ \begin{align*} & Q_{\text{in}}^{\text{(rev)}} > -Q_{\text{out}}^{\text{(irr)}} \\[15pt] \therefore ~ & Q_{\text{in}}^{\text{(rev)}} + Q_{\text{out}}^{\text{(irr)}} > 0 \end{align*} \]

式(10)および式(11)が示す結果を図で表したものが以下になります。

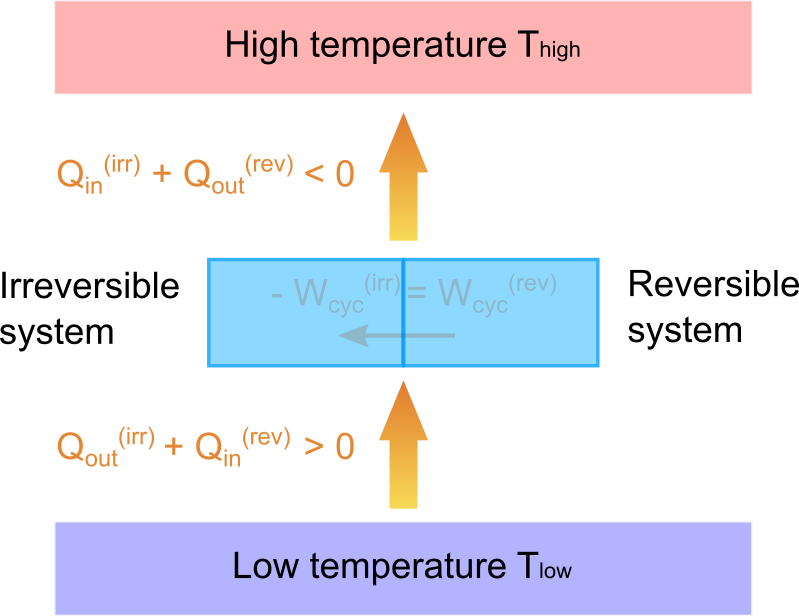
式(11)より2つのサイクルが連結された系は低温熱源から熱を吸収し、他方で式(10)より高温熱源に熱を逃がすという流れができあがります。

しかし、これは物理原則を破ってしまっています。

いま2つのサイクルが連結された系は外界との仕事のやり取りは一切なく、外から見れば単なる物体に過ぎません。

それにも関わらず、外からの仕事なしに熱が低温側から高温側に移動するというのは経験的にあり得ませんし物理原則を破ることになります。

つまり不可逆サイクルの熱効率が可逆サイクルの熱効率よりも大きくなるという条件設定は誤りであることが明かされます。

\(\eta_{\text{~irr}} = \eta_{\text{~rev}}\) のとき

最後に不可逆サイクルおよび可逆サイクルの熱効率がともに等しいと仮定した場合について考えておきます。

熱効率の条件を式(6)に適用した場合を考えると、

\[ Q_{\text{in}}^{\text{(irr)}} + Q_{\text{out}}^{\text{(rev)}} = 0 \]

が得られ、続けて式(12)と式(5)から

\[ Q_{\text{in}}^{\text{(rev)}} + Q_{\text{out}}^{\text{(irr)}} = 0 \]

を得ることができます。

つまり熱効率の等しい不可逆サイクルと可逆サイクルを連結した系では、それを運転させたとしても各熱源との正味の熱のやり取りは無いというのです。

しかし、どうもおかしい話だとは思わないでしょうか。

連結した系には不可逆な機構が含まれているのにも関わらず、運転させても全く影響を残さずそのままであるとは不自然でしょう。

実は後ほど示しますが、2つのサイクルを連結した系と熱源とが熱のやり取りを全くしないという状況は、可逆サイクルのみからなる系を利用した場合に実現されることなのです。

可逆サイクルはカルノーサイクルと熱効率が等しい

前節では不可逆サイクルと可逆サイクルを連結させた系について述べ、最後にそれを構成するサイクルの熱効率が等しい場合について取り上げました。

しかしその条件下では不可逆機構を含む連結系と熱源との間で熱のやり取りが一切行われないという不自然な結論が導かれました。

ですが、2つの可逆サイクルを連結させた系なら上記と同じ状況が許されます。

これを示す方法は、前述までに見てきたような物理の経験則を破っていないかという観点からの説明で可能です。

2つの可逆サイクルを用意し、それぞれを連結して1つの系として見ることもできるようにしておきます。

また、サイクルの間で生じる仕事は 2つのサイクルの間でやり取りを完結させ、外界への仕事は一切ないものとするのは これまでと同様です。

この連結した系は2つの可逆サイクルから構成されるので、順方向へも逆方向へも運転させることができます。

これが不可逆サイクルと可逆サイクルを連結した場合とは異なる点です。

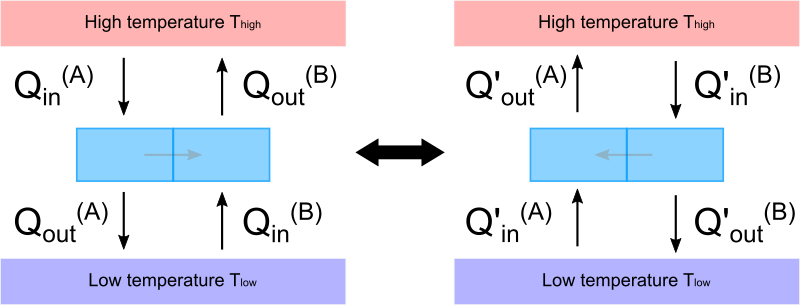
ではもし この2つの可逆サイクルを連結した系が、順方向あるいは逆方向のどちらかで高温熱源から低温熱源への熱移動を実現できたとするとどうなるでしょうか。

これはすなわち連結系をその逆方向に運転させれば、低温熱源から高温熱源へ熱移動を行えることを意味します。

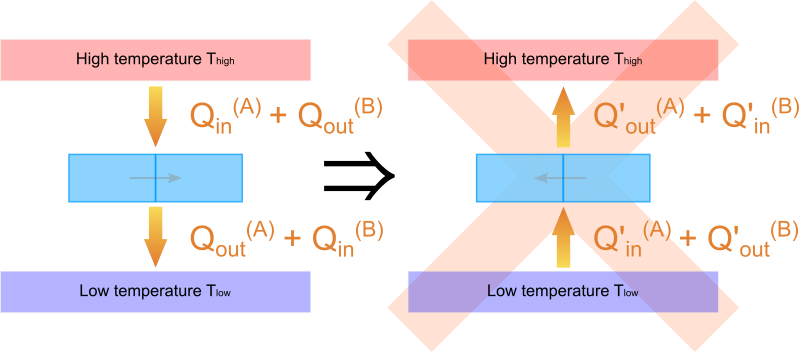
しかし前述の通り、この連結系は外界との仕事のやりとりを一切行いません。

にも関わらず、低温熱源から高温熱源への熱移動が行えるというのは物理原則に反することとなり不適当であると言えます。

つまり物理原則を破らないためには 連結系を運転させたときに熱源との正味の熱のやり取りが 0 であることが要求されるわけです。

\[ \begin{align*} & Q_{\text{in}}^{\text{(A)}} + Q_{\text{out}}^{\text{(B)}} = 0 \\[15pt] & Q_{\text{in}}^{\text{(B)}} + Q_{\text{out}}^{\text{(A)}} = 0 \end{align*} \]

したがって連結した2つのサイクルそれぞれの熱効率は共に等しい関係を得ることができます。

\[ \eta_{\text{A}} = \eta_{\text{B}} \]

さて、式(15)が得られましたが もう少し念を押して結果の意味を今一度しっかりと伝えておこうと思います。

重要な点は、2つの熱源間で動作する可逆サイクルについて述べている点と、着目している2つの可逆サイクルが具体的に何のサイクルであるかを特定していない点です。

例えば 2つの熱源間で動作するサイクルの代表例としてカルノーサイクルがありますが、

式(15)の結果によれば、2つの熱源で動作する任意の可逆サイクルもカルノーサイクルと同じ熱効率を持つことになります。

またカルノーサイクルのような熱から仕事を取り出すことのできるサイクルは他にもたくさん考えることができます。

ただしそれらは一般には2つの熱源のみでは可逆サイクルとして機能せず、逆操作を実現させるには無数の熱源を必要とします。

ここまでの結果はあくまでも2つの熱源間で動作するサイクルについて述べている点に注意して下さい。

※ちなみに2つの熱源によって可逆サイクルとして振る舞うものとして、スターリングサイクルやエリクソンサイクルなどが挙げられます。つまりこれらはカルノーサイクルと同じ最大熱効率を持つということです。

可逆サイクルの最大熱効率は作業物体によらない

ここまでの内容を理解していただければ、カルノーの定理の理解も容易になっているはずです。

当節では可逆サイクルの最大熱効率が作業物体によらないことを示します。

例によって2つの熱源間で動作する可逆サイクルを2つ用意します。

一方の系には作業物体Aを、他方には作業物体Bを用いて運転させるとしましょう。

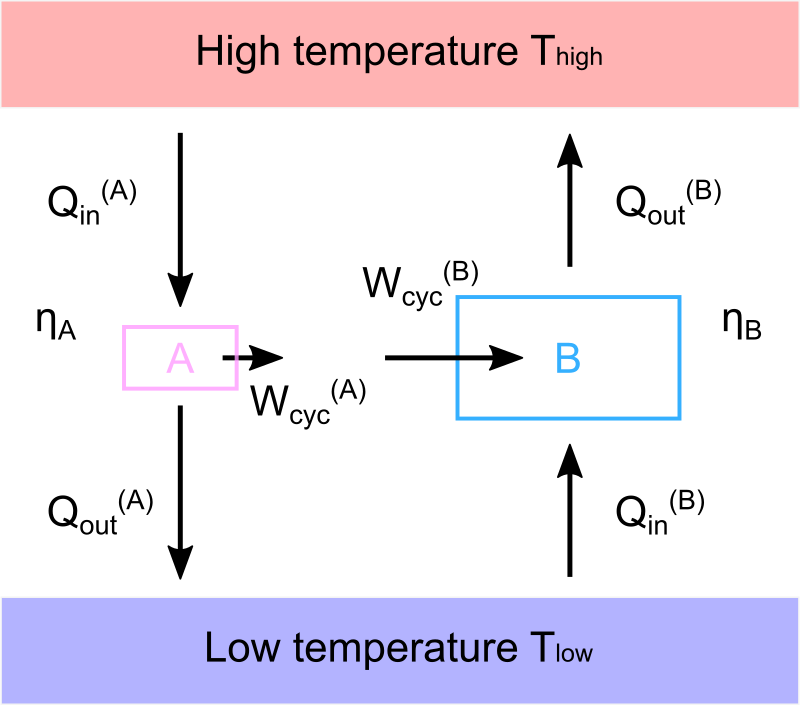
それぞれ用いる作業物体が異なるので熱効率 \(\eta_{\text{A}}\), \(\eta_{\text{B}}\) も異なると考えるのが普通な発想です。

\[ \eta_{\text{A}} = \frac{W_{\text{cyc}}^{\text{(A)}}}{Q_{\text{in}}^{\text{(A)}}}, ~~~ \eta_{\text{B}} = \frac{W_{\text{cyc}}^{\text{(B)}}}{Q_{\text{out}}^{\text{(B)}}} ~~~ ( ~ \eta_{\text{A}} ~ \char`≠ ~ \eta_{\text{B}} ~(?)~ ) \]

いま可逆サイクルAおよびBは 1 サイクル辺りで必要な仕事量の大きさが異なります。

前節までと同様に、一方のサイクルがする仕事すべてを もう一方のサイクルが受け取る状況を考えましょう。

例えば、仕事量には示量性があるので可逆サイクルAのサイズを \(k\) 倍にすれば、それに伴って仕事量も \(k\) 倍になります。

もしくは可逆サイクルAを \(k\) 回運転させて \(k W_{\text{cyc}}^{\text{(A)}}\) 分の仕事をさせても良いでしょう。

そのようにして得られた仕事を可逆サイクルBへすべて供給するので、式で表現すれば以下のようになります。

\[ k W_{\text{cyc}}^{\text{(A)}} = - W_{\text{cyc}}^{\text{(B)}} \]

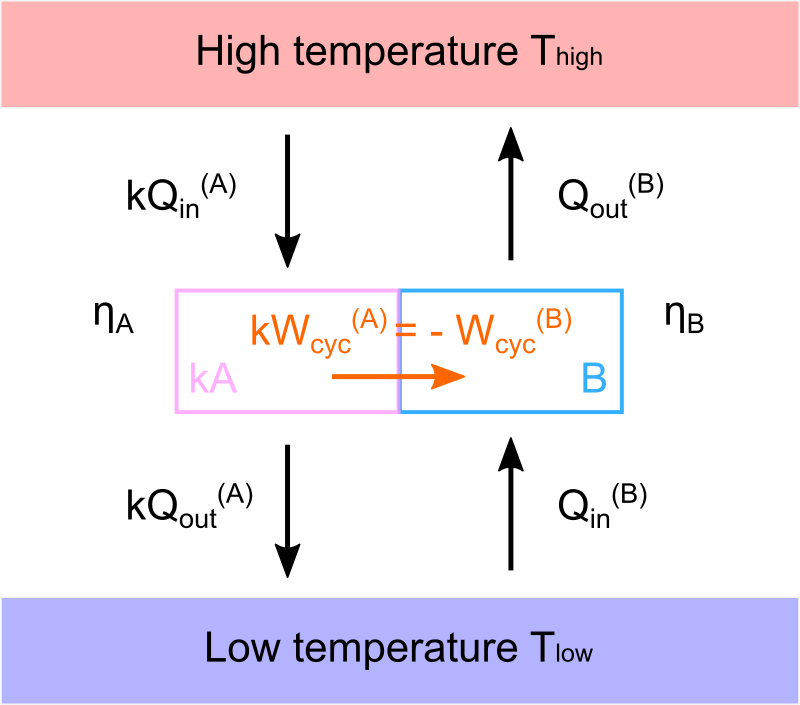
ちなみにですが、上記のように系のサイズを \(k\) 倍にしようが、\(k\) 回分のサイクルを考えようが熱効率は変化しません。

なぜなら熱量も示量性を持つため、式(16)より倍数分 \(k\) は分母分子でキャンセルされるからです。

話を戻しますが、続いて考えることは熱力学第一法則 \(\Delta U = -W + Q\) によるエネルギー保存です。これも前述と同じことの繰り返しですね。

可逆サイクルAおよびBについて次の2式が得られます。

\[ \begin{align*} 0 = - W_{\text{cyc}}^{\text{(A)}} + Q_{\text{in}}^{\text{(A)}} + Q_{\text{out}}^{\text{(A)}} \\[15pt] 0 = - W_{\text{cyc}}^{\text{(B)}} + Q_{\text{in}}^{\text{(B)}} + Q_{\text{out}}^{\text{(B)}} \end{align*} \]

式(17)および式(18)から仕事を消去して整理したものが次式です。

\[ (k Q_{\text{in}}^{\text{(A)}} + Q_{\text{out}}^{\text{(B)}}) + (Q_{\text{in}}^{\text{(B)}} + k Q_{\text{out}}^{\text{(A)}}) = 0 \]

前半のカッコと後半のカッコはそれぞれ、連結した系が高温熱源および低温熱源とやり取りする正味の熱量です。

いま、連結された系を構成する2つのサイクルは、ともに可逆サイクルであるために順方向と逆方向の両方の運転が可能です。

しかし前節の議論と同様に、もしどちらの運転によって高温熱源から低温熱源への熱移動が起きるとすると、その逆方向の運転によって外からの仕事なしに低温熱源から高温熱源への熱移動を実現することになります。

これは物理原則を破ることになるので、連結系と熱源との正味の熱のやり取りが 0 であることが要求されるのでした。

つまり式(19)で分けたカッコ内の熱量がそれぞれ

\[ \begin{align*} k Q_{\text{in}}^{\text{(A)}} + Q_{\text{out}}^{\text{(B)}} = 0 \\[15pt] Q_{\text{in}}^{\text{(B)}} + k Q_{\text{out}}^{\text{(A)}} = 0 \end{align*} \]

となれば良いのです。

あとは \(k\) について解いていくと、次に示す熱量比の関係を導くことができます。

\[ \begin{align*} k &= \frac{-Q_{\text{out}}^{\text{(B)}}}{Q_{\text{in}}^{\text{(A)}}} = \frac{Q_{\text{in}}^{\text{(B)}}}{-Q_{\text{out}}^{\text{(A)}}} \\[15pt] & \Leftrightarrow ~ \frac{Q_{\text{out}}^{\text{(A)}}}{Q_{\text{in}}^{\text{(A)}}} = \frac{Q_{\text{in}}^{\text{(B)}}}{Q_{\text{out}}^{\text{(B)}}} \end{align*} \]

さて式(21)が導けたところで、作業物体AおよびBを利用して運転させた可逆サイクルの効率が実は等しくなることを言うことができます。

それには式(18)を利用して熱効率の式(16)を次のように書き換えて見るとすぐさま理解できるでしょう。

\[ \begin{align*} \eta_{\text{A}} = \frac{Q_{\text{in}}^{\text{(A)}} + Q_{\text{out}}^{\text{(A)}}}{Q_{\text{in}}^{\text{(A)}}} = 1 + \frac{Q_{\text{out}}^{\text{(A)}}}{Q_{\text{in}}^{\text{(A)}}} \\[15pt] \eta_{\text{B}} = \frac{Q_{\text{in}}^{\text{(B)}} + Q_{\text{out}}^{\text{(B)}}}{Q_{\text{out}}^{\text{(B)}}} = 1 + \frac{Q_{\text{in}}^{\text{(B)}}}{Q_{\text{out}}^{\text{(B)}}} \end{align*} \]

熱効率を表す式に現れる熱量比はちょうど式(21)のものと一致しています。

したがって \(\eta_{\text{A}} = \eta_{\text{B}}\) という結論を導くことができるということです。

以上をまとめると、2つの熱源で動作する可逆サイクルの最大熱効率は、それに用いる作業物体の種類に依存せず常に等しい値を取ると言えます。

熱効率は2つの温度のみで決定される

ここまでに得られた結果を利用すれば芋づる式に重要な結論が導き出せます。

それがカルノーの定理 2つ目の主張である、2つの熱源で動作する可逆サイクルの最大熱効率が それら熱源の温度のみで完全に決定されるという内容です。

前節で示した 2つの熱源で動作する可逆サイクルの熱効率は作業物体によって変化しないことが肝になります。

これは言い換えると私達が扱いやすいと思う都合の良い物体を選択してよいということなのです。

つまりこういう事…。

2つの熱源で動作する任意の可逆サイクルは、なんと理想気体を作業物体として考えたときのカルノーサイクルの熱効率 ( 式(1) ) に等しくなる。

\[ \eta = \frac{W_{\text{cyc}}}{Q_{\text{in}}} = 1 - \frac{T_{\text{low}}}{T_{\text{high}}} \]

驚愕的な結果ではありますが、実際にカルノーサイクルと同じく2つの熱源で可逆サイクルとして振る舞うスターリングサイクルやエリクソンサイクルを理想気体に対して各自適用してみることをオススメします。

実際に式(1)と同じ結果が得られることを確認できるでしょう。

まとめ

2つの熱源で動作する可逆サイクルについて以下に示すカルノーの定理が成立します。

• 最大熱効率は作業物体によらない
• 最大熱効率は2つの温度のみで決まる

具体的には常に熱効率 \(\eta\) が次式で表現されることを意味します。

\[ \eta = 1 - \frac{T_{\text{low}}}{T_{\text{high}}} \]

ここで \(T_{\text{high}}\) は高温熱源の温度、\(T_{\text{low}}\) は低温熱源の温度です。