系が状態変化に伴って外界に仕事をするとき、どのような過程をたどってきたかで仕事量は異なります。

例えば次の \(P\) - \(V\) 図に示された2つの曲線。これは系が状態を変化する際にたどる経路を表しています。

系はどちらの経路をたどる場合でも変化前後の状態はともに同じですが、その間に外界に及ぼす影響はそれぞれの過程で異なるのです。

このような性質を経路依存性があるといい、経路に依らず変化前後の状態のみで決まる状態量とは対照的です。

当ページではなぜ仕事に経路依存性があるのか、仕事の定義から丁寧に解説をしていきます。

熱力学系が外界にする仕事

系の圧力が一定の場合

系が外界にする仕事 \(W ~ [\text{J}]\) は系の圧力 \(P ~ [\text{Pa}]\) と系の体積変化 \(\Delta V ~ [\text{m}^3]\) の積で表すことができます。

\[ W = P \Delta V \]

式(1)は次に示す古典力学における仕事の定義から導くことが可能です。

\[ W = F \Delta x \]

\(F ~ [\text{N}]\) ピストンに加わる力、\(\Delta x ~ [\text{m}]\) はピストンの変位を表しています。

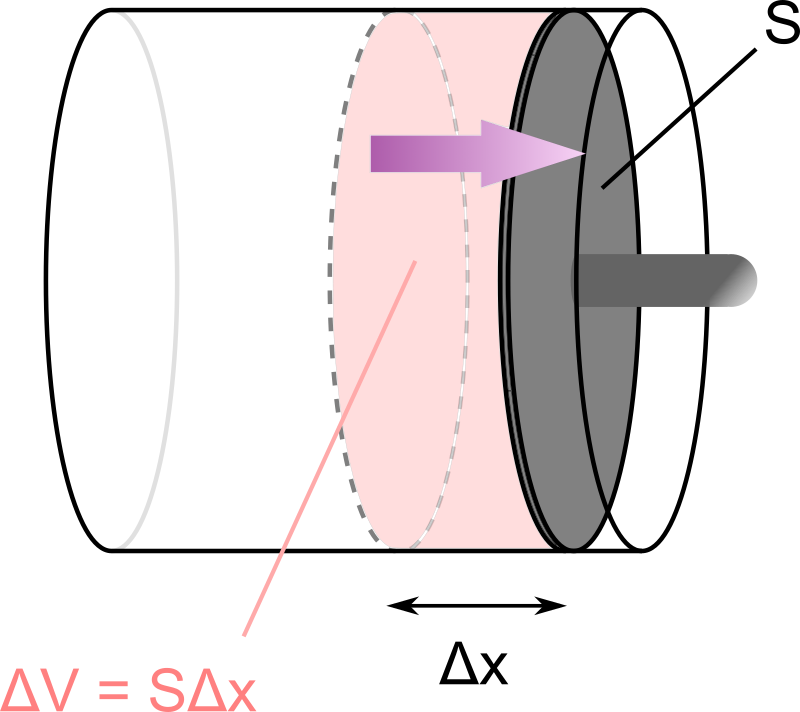
ピストンに加わる力 \(F\) は、系の圧力 \(P ~ [\text{Pa}]\) とピストンの断面積 \(S ~ [\text{m}^2]\) を用いて \(F = PS\) と表現できるので、仕事の定義式は次のようになります。

\[ W = PS \Delta x \]

また断面積と変位の積 \(S \Delta x\) は、次の図のようにピストンを動かすことによって生まれる空間を表しているので、\(S\Delta x = \Delta V\) とすれば、式(1) \(W = P \Delta V\) が導けた事になります。

ただし式(1)は系の圧力が一定の場合でしか適用することができません。

例えば、外から一定の圧力を加えた状況で系の温度を操作して体積変化させた際の仕事は式(1)で計算可能です。

系の圧力が一定ではない場合

しかし系の圧力が一定に保たれるのは上記で説明したような限られた場合であり、一般には系の状態が変化すると圧力も同時に変化します。

それだけでなく系が状態変化する間は内部が非平衡状態となるので、そもそも状態量である圧力 \(P(T; ~ V, ~ n)\) が定義できないといった問題もあるのです。

では系が外界にする仕事を数学的に扱うことはできないかと言うと…微小操作を考えることで解決できます。

微小操作では系内部への影響が非常に小さく、ほとんど平衡状態が崩れることがありません。

つまり圧力 \(P(T; ~ V, ~ n)\) の定義が許容されるのです。

加えて、微小操作の間では圧力変化が小さくほぼ一定とみなせます。

すると圧力一定の場合に成立する式(1)のように、系がする仕事は圧力と体積変化の積で表すことが可能になります。

\[ \delta W = P dV ~~~ ( ~ P = P(T; ~ V, ~ n) ~ ) \]

と書けます。

通常、微小量を表す際は \(d\) を用いますが、微小仕事には \(\delta\) を用いました。

これは仕事が状態量ではなく、経路依存性を持つことを忘れないためです。

系がする仕事は、上記のように体積変化が微小な場合のみにしか適用できないように思われるかもしれません。

しかし、この微小仕事を繰り返し連続的に行うことによって、体積変化が大きな場合でも仕事を計算することが可能です。

それは数学的には微小仕事の和として表現でき、更にそれは積分で書き換えることができます。

\[ \begin{align*} W &= \lim_{\Delta V_i \rightarrow 0} \sum_{i = 1}^N P \Delta V_i \\[15pt] W &= \int_{V_\text{A}}^{V_\text{B}} P dV \end{align*} \]

式(5)で表される仕事は最大仕事とよばれ、系が外界にし得る最大の仕事量となります。

仕事の経路依存性

冒頭でも述べたとおり、系の状態変化に伴う仕事は、たどった過程によって仕事量は異なります。

このことを、仕事には経路依存性があると言います。

そして仕事に経路依存性があることは、前節までに示してきた仕事の式から理解できます。

\[ \begin{align*} W &= P \Delta V \\[15pt] W &= \int_{V_\text{A}}^{V_\text{B}} P dV \end{align*} \]

仕事は圧力と体積変化の積あるいは積分で表されますが、これは見方を変えれば \(P\) - \(V\) 図上の面積として解釈することができます。

ここで冒頭で示した図に戻ります。

それは系をある平衡状態から別の平衡状態へ変化させる際に、2つの異なる経路を考えたものでした。

系がする仕事は、たどった経路と横軸に挟まれる面積と見ることができるので、図示したものが次です。

上図から直ちに理解できますが、それぞれの経路がつくる面積の大きさは全く異なります。

つまり系が外界にする仕事は、状態変化の際にたどる経路によって異なる値をとる事が分かるでしょう。

またそれぞれの過程で系がする仕事は変化前後の平衡状態に依らないことから、仕事が状態量ではない事も示されます。

まとめ

熱力学系がする仕事は、系が状態変化する際にたどった経路によって異なる値を取ります。

これを「仕事は経路依存性がある」と言って、変化前後の系の平衡状態によって決まる状態量とは対照的です。

熱力学系が外界にする仕事 \(W\) は、数学的には系の圧力 \(P\) と体積変化 \(\Delta V\) の積で与えることができます。

\[ W = P \Delta V \]

ところが上記は系の圧力が一定のときにしか利用できず、一般に系の状態変化に伴って圧力も変化するものです。

そのため圧力変化がほとんど無視できるような微小な操作を考えれば、微小仕事として次のように表現できます。

\[ \delta W = P dV \]

仕事は経路依存性があることを明示するために、微小量であることを表す \(d\) の代わりに \(\delta\) を利用することが一般的です。

また微小操作を繰り返し行うことによって、大きな体積変化を伴う場合でも系が外界にする仕事を求めることができます。

\[ W = \lim_{\Delta V_i \rightarrow 0} \sum_{i = 1}^N P \Delta V_i = \int_{V_\text{A}}^{V_\text{B}} P dV \]

また上記の仕事は、熱力学系が外界にし得る最大の仕事量であり最大仕事と呼ばれます。