熱力学系が外界にし得る仕事量には上限があり、その仕事を最大仕事と言います。

また系が最大仕事をするとき、その過程で系の平衡状態は保たれるという主張があり、これを最大仕事の原理と言います。

一般に系を操作したとき系は必ず非平衡状態となりますが、上記の様な過程を再現する操作として準静的操作があります。

最大仕事の原理

熱力学系が外界にし得る仕事量には上限があり、その仕事を最大仕事と言います。

次の様な平衡状態A \((T_\text{A}; ~ V_\text{A}, ~ n_\text{A})\) から平衡状態B \((T_\text{B}; ~ V_\text{B}, ~ n_\text{B})\) への力学的操作を考えましょう。

\[ (T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) ~ \rightarrow ~ (T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) \]

ここで重要なことは、操作前後における平衡状態は定まっていますが、その間の過程については何も言及されていない点です。

この操作(1)を実際に行うにはいくつか方法が考えられます。

図のように状態Aと状態Bを結ぶ曲線は、それぞれが操作(1)の最中に系がたどった過程を表しています。

そして図中には1つだけ実線で表した曲線があり、この経路を経由したとき系は外界に最大仕事をします。

逆に破線で示された経路をたどってきた系は、最大仕事以下の仕事しかできません。

なぜ経路ごとに系がする仕事が変化するのかと言うと、仕事には経路依存性という性質があるためです。

一般に系がする仕事 \(W\) は最大仕事 \(W_\text{max}\) 以下ということなので、数学的には以下の通りになります。

\[ W \leq W_\text{max} ~~~ \left( ~ W_\text{max} = \int_{V_\text{A}}^{V_\text{B}} P dV ~ \right) \]

最大仕事は具体的にはカッコで示した様になります。これは後ほど説明をするので現時点では雰囲気だけ雰囲気だけ掴んでおいて下さい。

では、実線と破線の違いとは何かを説明します。

図中の曲線は操作の最中に系がたどった過程というのは前述通りで、

中でも系の平衡が常に保たれた過程を実線で、非平衡状態となった過程を破線で表しています。

• 実線 : 操作の最中、系内部は平衡状態を保持
• 破線 : 操作の最中、系内部は非平衡状態

また前述のとおり、系が実線の過程を経由するとき、系は外界に最大仕事をするのでした。

つまりまとめると、系が状態を変化させる過程において常に平衡状態が保たれているとき、系は外界に最大仕事をするということです。

これを最大仕事の原理と言います。

逆に、操作の最中に非平衡状態となる場合、系がする仕事は最大仕事よりも小さくなるという事も同時に言えます。

また平衡状態は \((T; ~ V, ~ n)\) というように唯一の状態を指すのに対し、非平衡状態はあらゆる状況が考えられます。

つまり操作の最中に非平衡状態となる場合、実際はどのような過程を経由したかを正確に定めることはできません。

そのため \(P\) - \(V\) 図上では系が経由したであろう経路を便宜的に破線で表現をしています。

そして非平衡状態を経由する過程は、その複雑さ故に無数に存在します。同様にして状態Aと状態Bの間を結ぶ破線もまた無数に存在するという事です。

準静的操作

最大仕事の原理によれば、系が最大仕事をするとき系の平衡は常に保たれる必要があるようですが、これは熱力学系で観測される一般的事実を考慮すると随分と大胆な主張です。

なぜなら系を操作すると、少なくとも系は非平衡状態となるためです。

一体どういうことなのでしょうか。

この疑問を解消する上で重要になるのは最大仕事はどのように得られるかです。

こちらで説明するように、最大仕事は微小仕事の積分として得られます。

微小仕事とは、内部の圧力 \(P\) と微小体積変化 \(dV\) の積で与えられ

\[ \delta W = P dV \]

この微小体積変化、すなわち微小操作を系が任意の体積になるまで繰り返せば、その過程で系が外界にした仕事を表現できます。

\[ W_\text{max} = \int_{(T_\text{A}; ~ V_\text{A}, ~ n_\text{A})}^{(T_\text{B}; ~ V_\text{B}, ~ n_\text{B})} \delta W = \int_{V_\text{A}}^{V_\text{B}} P dV \]

これが式(1)でも示した最大仕事の具体的な表式です。

また微小操作の繰り返しとは、長い時間をかけて静かに系を操作するといった状況をイメージすれは良いでしょう。

このように操作することで平衡状態の崩れを最小限に抑えることができます。

また上記の内容を図解すると次のようになります。

系の体積を段階的に微小変化させていき、その時々の平衡状態を表したものが図中の各点です。点と点の間は操作途中の非平衡状態を指しているので \(P\) - \(V\) 図上には表現することはできません。

これよりも更に微小操作の幅を細かくすれば点の数は増えていき、その点の集合は1つの曲線としてみなせるようになります。

こうして得られる滑らかな曲線の存在は、系が常に平衡状態であることを意味する他はありません。

しかしあくまでもコレは数学的極限の話であり、現実には平衡が常に保たれる操作は存在しません。

この極限的状況を再現するためには、1つ目の図で示すような段階的な操作を行うのが賢明です。操作中に系はほとんど平衡状態を保つことから準静的操作と呼ばれます。

また準静的操作は、逆向きの操作も可能です。

状態Aから段階的に状態Bにたどって来れたのと同様に、状態Bから状態Aに戻っていくこともまたできます。

この操作は両頭矢印を用いて次のように表現すると便利です。

\[ (T_\text{A}; ~ V_\text{A}, ~ n_\text{A}) ~ \leftrightarrow ~ (T_\text{B}; ~ V_\text{B}, ~ n_\text{B}) \]

まとめ

ここで、上記までの内容を表にまとめておきます。

	準静的操作	準静的ではない操作
系がする仕事	\(W = W_\text{max}\)	\(W < W_\text{max}\)
内部の状態	平衡状態	非平衡状態

準静的操作によって系は平衡状態をほとんど崩すことなく外界に最大仕事しますが、

逆に準静的ではない操作をするとき、系の平衡は崩れ、外界にする仕事も最大仕事より小さくなります。

準静的ではない操作とは、準静的操作の裏であると考えると、急激で素早い操作などが挙げられます。

このように熱力学系は操作の仕方に敏感に影響することが分かります。

次節では気体を例にして、上記の内容が現象としてどのように説明されるのかを図を用いて理解することを試みます。

操作の違いによる気体の挙動

ここからは気体が封入された容器への操作を考えます。

ピストンを動かして系を準静的に操作する場合とそうではない場合に分け、気体がどのように振る舞うのかを理解しましょう。

以降では、準静的操作を「長い時間を掛けて静かに行う操作」、一方で準静的ではない操作を「急激な素早い操作」であるとして話を進めていきます。

準静的操作の場合

準静的にピストンを静かに操作する場合、系は平衡状態を保ちながら外界に最大仕事をします。

気体はほんの少しの力を加えただけで複雑に流動してしまいますが、ピストンを静かに動かすことによってそれを抑制できます。

次の図はピストンを静かに動かして系の体積を膨張・圧縮させた場合の様子を表したものです。

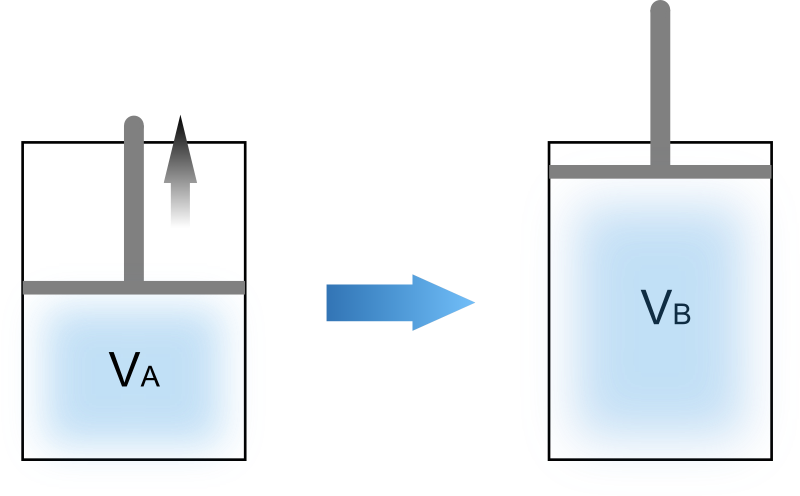
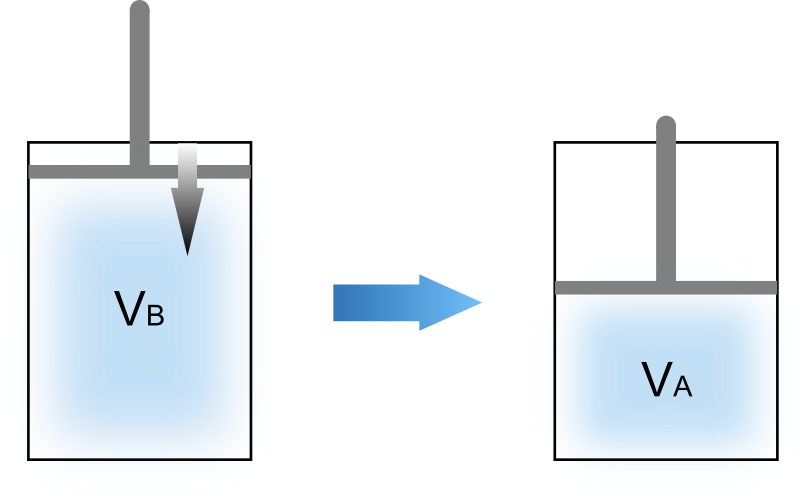
準静的過程では操作の途中でほとんど平衡が崩れないため、容器内は均一な状態が保たれます。

そして重要であるのは操作の最中に気体がピストンに接していることです。

気体がピストンに接した状態であれば、気体はピストンに対して必要十分な仕事をします。すなわちこれが最大仕事ですね。

この事は後に説明する準静的操作ではない場合と比較すればより理解しやすくなります。

また興味深いことに、膨張時と圧縮時における最大仕事を \(W_\text{max}^{{\text{A} \rightarrow \text{B}}} > 0\)、\(W_\text{max}^{\text{B} \rightarrow \text{A}} < 0\) としたとき次の関係が成立します。

\[ W_\text{max}^{{\text{A} \rightarrow \text{B}}} + W_\text{max}^{\text{B} \rightarrow \text{A}} = 0 \]

これは系が準静的操作によって状態Aと状態Bの間を行き来できる可逆過程となっているためです。

詳細はこちらで解説しています。

準静的ではない操作の場合

系に対する操作が準静的ではない場合、系は非平衡状態となり外界にする仕事は最大仕事より小さくなります。

ピストンを素早く動かして系を膨張させたり圧縮したりすると、次の図のように容器内の気体は複雑に流動して不均一な状態になります。

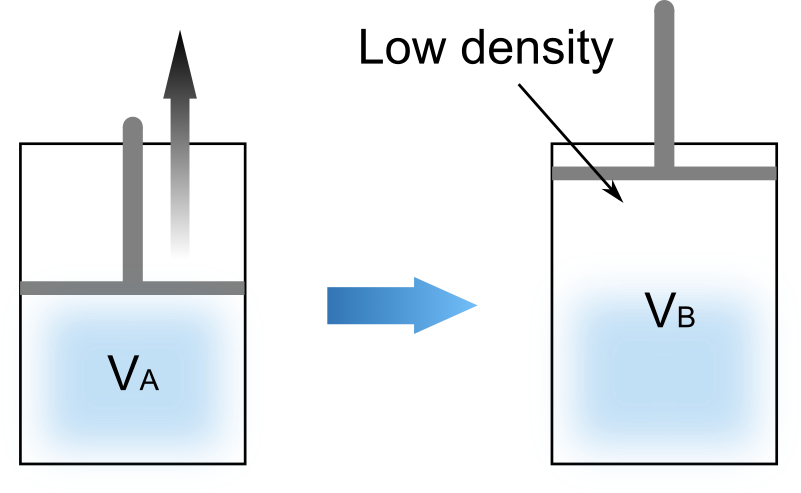
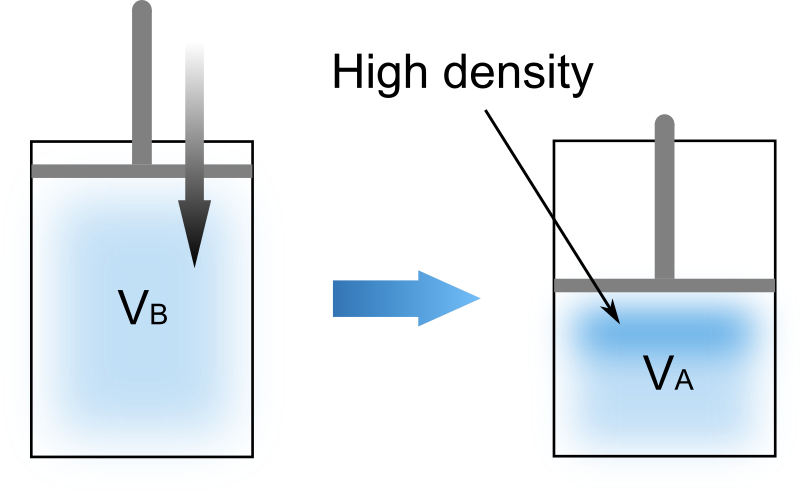
上図は状況を簡略的に表現したものですが、準静的な操作と比較して内部の気体はピストンの動きに追いつけず不均一になります。

結果ピストン付近の気体の密度は、均一な場合よりも上がるもしくは下がります。

• 膨張過程 : ピストン付近の気体密度が低下
• 圧縮過程 : ピストン付近の気体密度が上昇

非平衡状態を経由する場合、系がする仕事が最大仕事より小さくなる原因はまさにコレなのです。

膨張過程では、気体はピストンを十分に押すことができないため、最大仕事 \(W_\text{max}^{{\text{A} \rightarrow \text{B}}}\) よりも小さな仕事になります。

同様に圧縮過程では気体は外界から仕事され過ぎるので、これも圧縮時における最大仕事 \(W_\text{max}^{\text{B} \rightarrow \text{A}}\) よりも小さな値を取るようになります。

以上を数学的にまとめると、膨張および圧縮過程での仕事 \(W^{\text{A} \rightarrow \text{B}}\)、\(W^{\text{B} \rightarrow \text{A}}\) が最大仕事以下となるので次のように記述できるわけです。

\[ \begin{align*} 0 < W^{\text{A} \rightarrow \text{B}} < W_\text{max}^{\text{A} \rightarrow \text{B}} \\[15pt] W^{\text{B} \rightarrow \text{A}} < W_\text{max}^{\text{B} \rightarrow \text{A}} < 0 \end{align*} \]

これは最大仕事の原理を満たしていますよね。

こうして気体の挙動として視覚的に理解することで、最大仕事の存在や、最大仕事の原理は比較的理解しやすくなるでしょう。