相平衡とは

容器に入れられた水の一部を取り出したとして、その水は容器に残された水と全く同じ性質を持ちます。

これは容器内の水が一様になっているためであり、そのような形態のことを相と言います。

水の場合 大気圧下で 0 \([^\text{o}\text{C}]\) に冷やすと氷に変化し、逆に 100 \([^\text{o}\text{C}]\) に熱すると水蒸気になるように、物質は固体・液体・気体の物理状態を取り得ます ( 例外もあります )。

その物理的様子から、それぞれの形態は固相、液相、気相と呼ばれます。

そしてこれらは単一で存在する以外に、2相ないし3相と複数の相で共存する場合があり、各相の熱力学的状態がつり合った状況を相平衡と言います。

以下で例を示しながら詳細を解説していきます。

気相と液相の共存 : 気液平衡

気相と液相が共存する平衡状態のことを気液平衡と言います。

例えば水と水蒸気 ( のみ ) が入れられた容器を考えましょう。

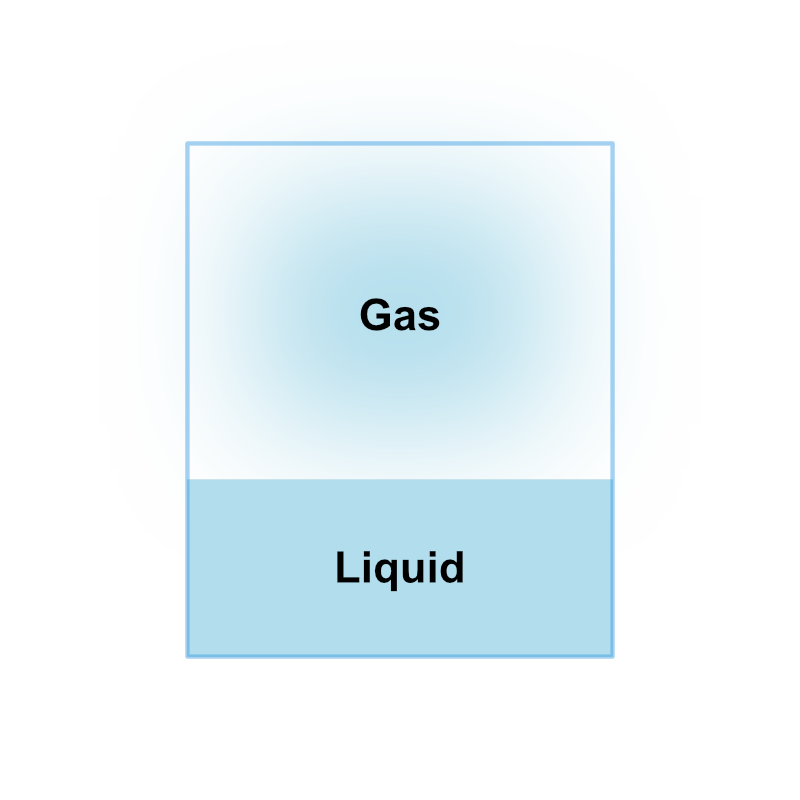
水および水蒸気は系の状態 \((T, ~ P)\) によって蒸発したり凝結するためすることによって水蒸気に変化することも、水蒸気から凝結して水に変化することができます。

気液平衡ではこれらがちょうどつり合っており、見かけ上変化していない様に見えるのです。

また気相に存在する蒸気が示す圧力を蒸気圧と呼ぶことも合わせて覚えておきたい内容です。

蒸気圧には興味深い特徴があり、系が気液平衡状態にあるとき温度 \(T\) に対して必ず一意の値を取るのです。

例えば同じ温度 \(T\) の条件の下で多量の水が入った容器と少量の水が入った容器2つを考えたとき、それぞれ気相が示す蒸気圧は等しくなります。

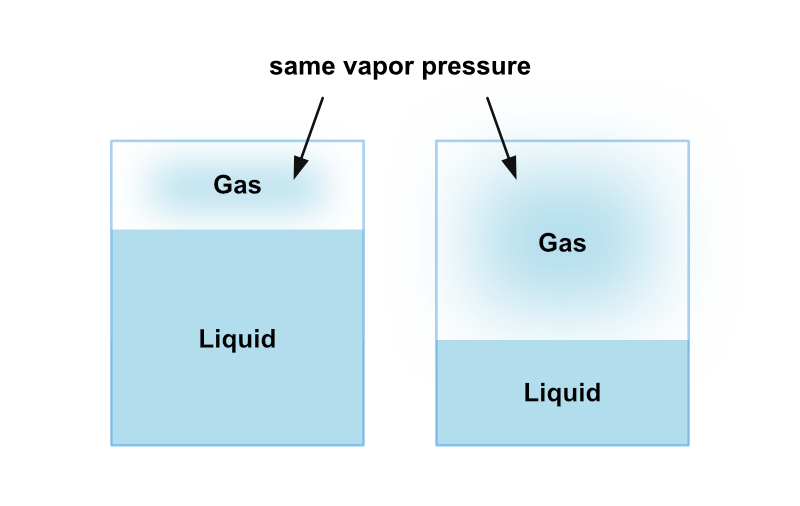
このときの蒸気圧を飽和蒸気圧と言って、その温度に対する蒸気圧の上限値を表しています。

これは言い換えると、系をある温度に設定した時点で気相に存在し得る最大蒸気量が決まってしまうという事です。

液相と固相の共存 : 固液平衡

液相と固相が共存する平衡状態のことを固液平衡と言います。

例えば水に氷を浮かべた状況はまさに固液平衡状態に当たります。

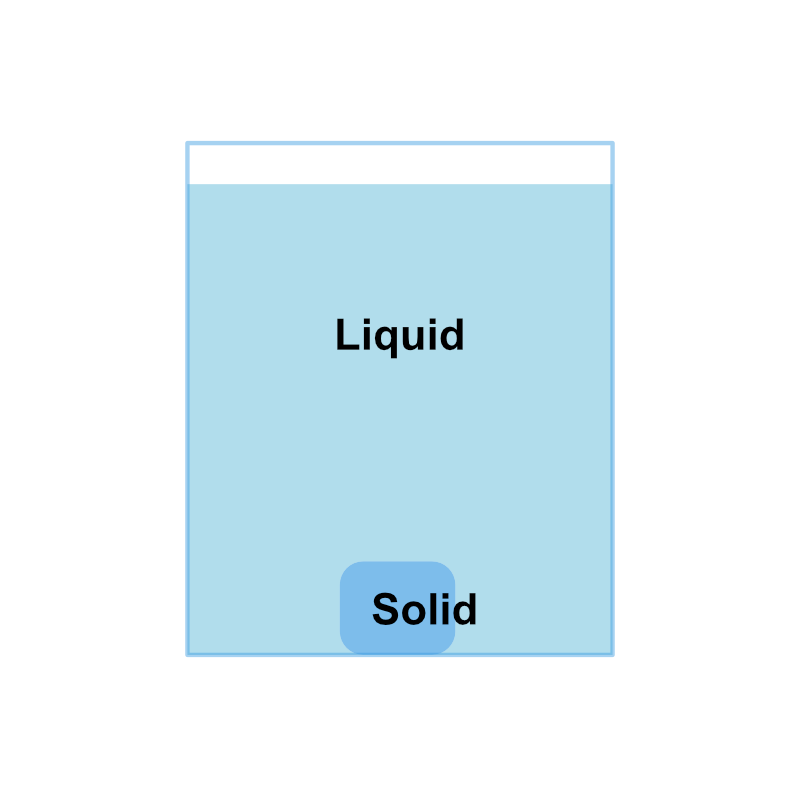
固液平衡状態とは、固体が融解して液体になる状態変化と、液体が凝固して固体になる状態変化がちょうどつり合った状況を指します。

適切な温度に調整しなければ、

ただし氷水を室温 ( 25 \([^\text{o}\text{C}]\) ) 程度に置いておくと自然に氷が融解して水のみになることを経験的に知っている通り、この温度条件では氷水の平衡状態を保つことはできません。

氷水の固液平衡の実現には、室温よりも温度を下げる必要があります。

気相と固相の共存 : 固気平衡

気相と固相が共存する平衡状態のことを固気平衡と言います。

物質が固体から液体を経由せずに気体になることを昇華と言いますが、例えばドライアイスや防虫剤は昇華性物質の代表です。

次の図を見ていただきましょう。

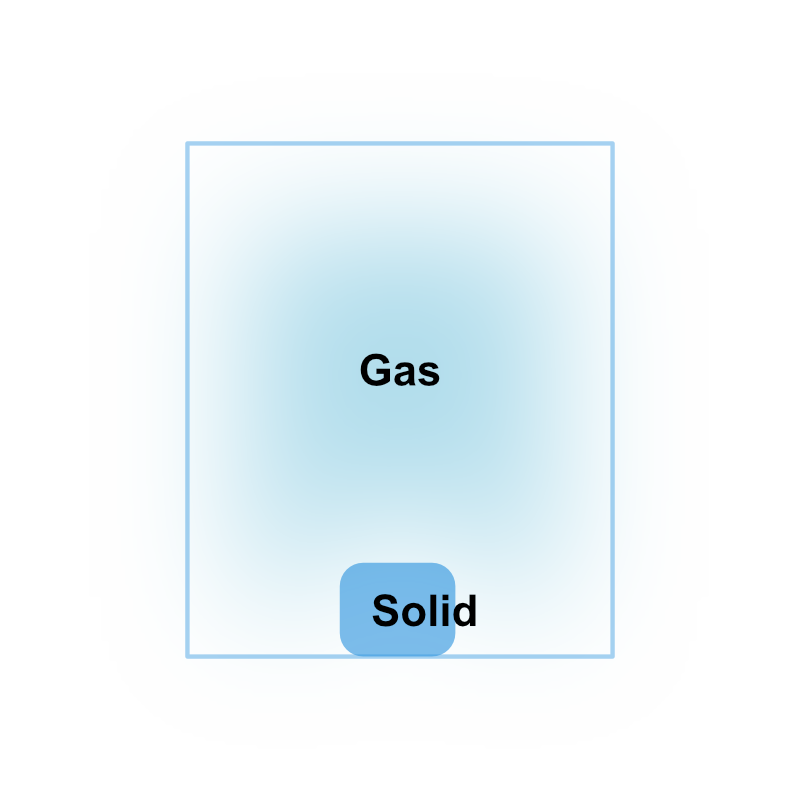
固気平衡状態は、固体から気体への変化およびその逆の変化がつり合ったときに実現されます。

当然扱う物質にも依りますが、室温程度では通常固体から気体への変化が優勢となる場合が多いので、固気平衡状態の実現には系の温度を極めて低く設定することが要求されます。

気相・液相・固相の共存 : 三重点

相平衡は何も2つの相の間で成立する現象ではなく、条件さえ揃えば複数の相で生じることもあります。

例えば、気相・液相・固相の3つの相が共存する温度・圧力条件があり、それを三重点と呼びます。

後ほど詳しく説明をしますが、「三重"点"」と呼ばれる理由は限定された条件でのみ見られるために、図に示したときに点として表現されるためです。

相の境界 : 界面

前節までは相について述べてきましたが、相と相の境界も非常に興味深い現象が観測されるために専門的な学問領域として発展しています。

この相の境界は「界面」と呼ばれ、界面に関する学問領域として界面物理学や界面化学があります。

ここでは界面現象の解説は割愛しますが、「界面」という用語を知っておいて損は無いでしょう。

相平衡の数学的記述

系が異なる相を持って平衡に達するためには、特定の温度・圧力条件を満たす必要があります。

ここでは相平衡を数学的に記述することを考えていきます。

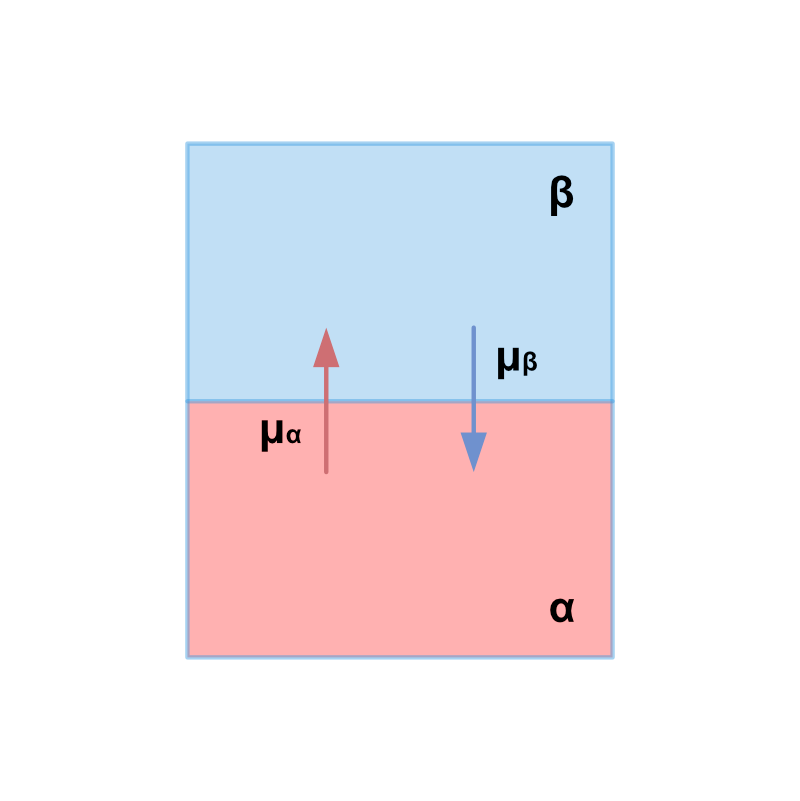
早速ではありますが、次の関係式は \(\alpha\) 相と \(\beta\) 相が温度 \(T\) および圧力 \(P\) の条件下で相平衡状態にあるとき成立します。

\[ \mu_\alpha (T, ~ P) = \mu_\beta (T, ~ P) \]

化学ポテンシャルとは物質移動の方向性を教えてくれる物理量であり、式(1)は \(\alpha\) 相からの物質移動と \(\beta\) 相からの物質移動がちょうどつり合っていることを表しています。

また2相平衡が成立する温度・圧力条件は \((T, ~ P)\) だけではありません。

ここから温度を \(dT\) だけ、また圧力を \(dP\) だけ変化させた状況 \((T + dT, ~ P + dP)\) を考えていきます。

変化後の条件においても2相平衡にあれば次式が成立します。

\[ \mu_\alpha (T + dT, ~ P + dP) = \mu_\beta (T + dT, ~ P + dP) \]

式(2)をテイラー1次近似を用いて展開すると、次のように式変形できます。

\[ \mu_\alpha(T, ~ P) + \left( \frac{\partial \mu_\alpha}{\partial T} \right)_P dT + \left( \frac{\partial \mu_\alpha}{\partial P} \right)_T dP = \mu_\beta(T, ~ P) + \left( \frac{\partial \mu_\beta}{\partial T} \right)_P dT + \left( \frac{\partial \mu_\beta}{\partial P} \right)_T dP \]

式(3)に含まれる \(\mu_\alpha (T, ~ P)\) および \(\mu_\beta (T, ~ P)\) は条件変化前における化学ポテンシャルのことで、これらは式(1)から消去されるので

\[ \left( \frac{\partial \mu_\alpha}{\partial T} \right)_P dT + \left( \frac{\partial \mu_\alpha}{\partial P} \right)_T dP = \left( \frac{\partial \mu_\beta}{\partial T} \right)_P dT + \left( \frac{\partial \mu_\beta}{\partial P} \right)_T dP \]

そして化学ポテンシャルの偏微分はモルエントロピー \(\left( \frac{\partial \mu}{\partial T} \right)_P = -\bar{S}\) およびモル体積 \(\left( \frac{\partial \mu}{\partial P} \right)_T = \bar{V}\) に等しいので、式(4)は次のように整理できます。

\[ \begin{gather*} -\bar{S}_\alpha dT + \bar{V}_\alpha dP = -\bar{S}_\beta dT + \bar{V}_\beta dP \\[15pt] \Leftrightarrow ~ (\bar{V}_\beta - \bar{V}_\alpha) dP = (\bar{S}_\beta - \bar{S}_\alpha) dT \\[15pt] \therefore ~ \frac{dP}{dT} = \frac{\bar{S}_\beta - \bar{S}_\alpha}{\bar{V}_\beta - \bar{V}_\alpha} \end{gather*} \]

得られた微分方程式(5)を解くことで温度の関数として圧力 \(P = P(T)\) が求められます。

\(P\) - \(T\) 図上に曲線として表したものを以降「共存線」と呼ぶことにしましょう。

共存線の具体的な求め方は次節で詳しく解説していきます。

相平衡を表す曲線を状態図に表現する

系を構成する物質がある条件下でどのような物理状態をとっているかを図で表したものを状態図と言います。

状態図は微分方程式(5)から計算できる共存線のいくつかを組み合わせることで作ることができます。

この状態図を利用すれば、ある温度・圧力条件 \((T, ~ P)\) において、対象の物質が気体・液体・固体のどの状態にあるか？ 或いは2相平衡の状態にあるのか？ はたまた3相平衡か？ といった判断を視覚的に行うことができるようになります。

以下では次の3つの場合

• 固液平衡について ( 固液共存線 )
• 気液平衡について ( 気液共存線 )
• 固気平衡について ( 固気共存線 )

それぞれ共存線を求めていきます。

このとき重要になるのは微分方程式(5)右辺にある、物質が \(\alpha\) 相から \(\beta\) 相へ状態変化する際のエントロピー変化 ( \(\bar{S}_\beta - \bar{S}_\alpha\) ) および体積変化 ( \(\bar{V}_\beta - \bar{V}_\alpha\) ) がどのような温度依存性を示すかです。

これらが上記3つの状況下でどのように表されるのかを見ていきましょう。

固液共存線の導出

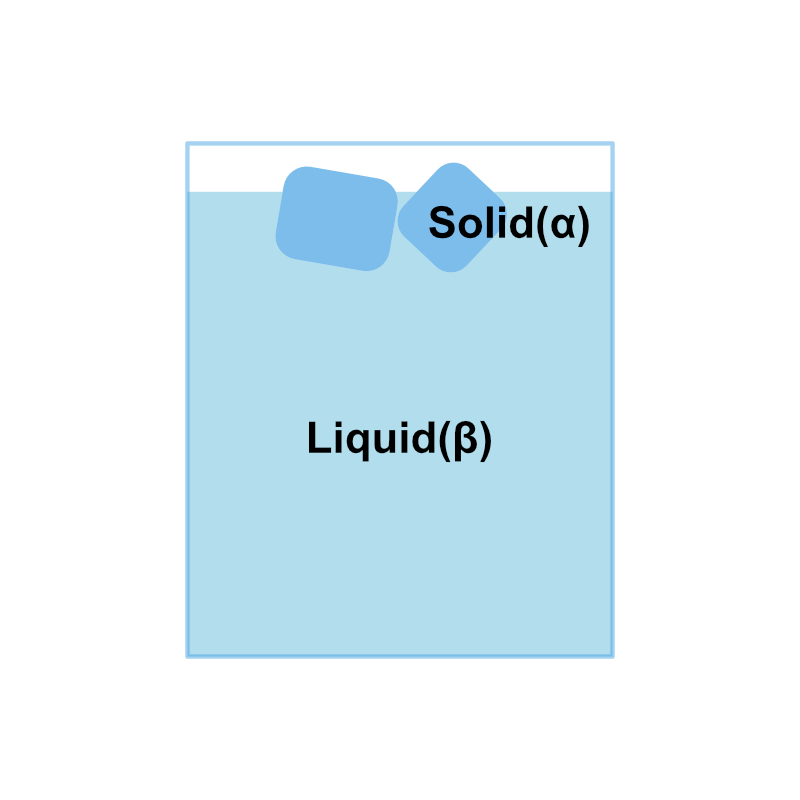
固相と液相が共存する固液平衡状態について考えます。

\(\alpha\) 相を固相、\(\beta\) 相を液相であるとすれば、物質の融解エントロピー \(\Delta \bar{S}_\text{m}\) と融解による体積変化 \(\Delta \bar{V}_\text{m}\) を求めることになります。

また物質が融解する間は一定温度 \(T\) に保たれるので、融解エントロピー \(\Delta \bar{S}_\text{m}\) は融解エンタルピー \(\Delta \bar{H}_\text{m}\) を温度で割った次式で表されます。

\[ \Delta \bar{S}_\text{m} = \bar{S}_\beta - \bar{S}_\alpha = \frac{\Delta \bar{H}_\text{m}}{T} \]

一方、融解による体積変化については実験的に測定 ( もしくは文献値を利用 ) する必要があります。

※系が平衡状態にあるときエントロピー変化は \[ \Delta S = \int \frac{\delta Q}{T} \] で与えられます。温度が一定であれば \[ \Delta S = \frac{Q}{T} \] となるのでした。系外から一定の圧力が加わっている場合、吸熱量 \(Q\) はエンタルピー変化 \(\Delta H\) に等しいので総平衡状態にあるエントロピー変化は \[ \Delta S = \frac{\Delta H}{T} \] と表すことができます。

式(6)を式(5)に代入すれば以下の式が得られます。

\[ \frac{dP}{dT} = \frac{\Delta \bar{H}_\text{m}}{T \Delta \bar{V}_\text{m}} \]

微分方程式(7)を解くにあたり、融解エンタルピー \(\Delta \bar{H}_\text{m}\) および融解による体積変化 \(\Delta \bar{V}_\text{m}\) が一定値とみなせる温度範囲で積分することにすると…

\[ \begin{gather*} \int_{P'}^P dP = \int_{T'}^T \frac{\Delta \bar{H}_\text{m}}{T \Delta \bar{V}_\text{m}} dT \\[20pt] \therefore ~ P(T) = P' + \frac{\Delta \bar{H}_\text{m}}{\Delta \bar{V}_\text{m}} \ln \frac{T}{T'} \end{gather*} \]

となって、固液共存線を導くことができます。

気液共存線の導出

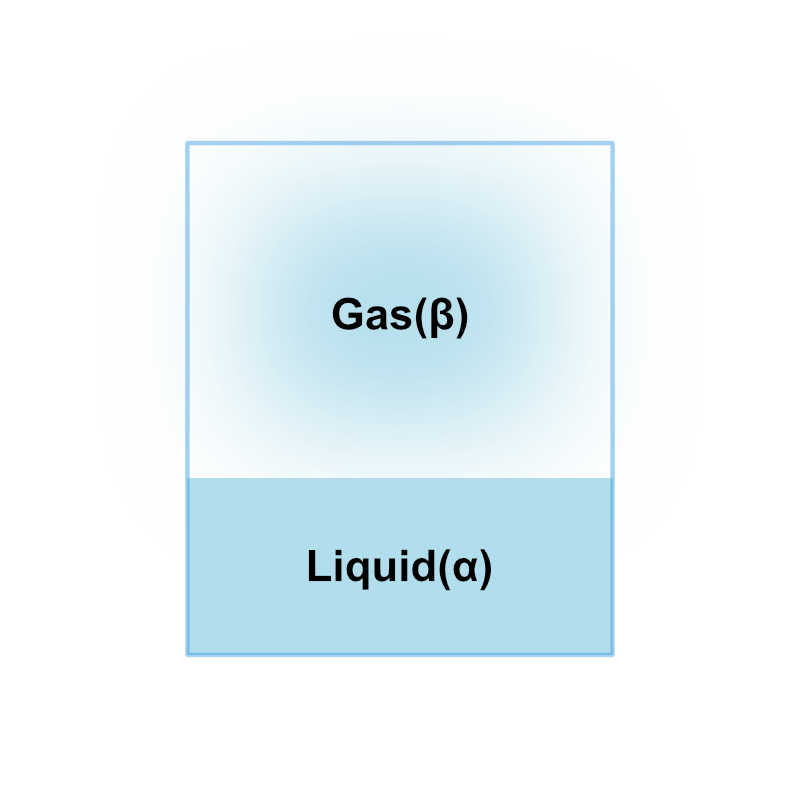
気相と液相が共存する気液平衡状態について考えます。

\(\alpha\) 相を液相、\(\beta\) 相を気相であるとすれば、物質の蒸発エントロピー \(\Delta \bar{S}_\text{v}\) と蒸発による体積変化 \(\Delta \bar{V}_\text{v}\) を求めることになります。

蒸発エントロピー \(\Delta \bar{S}_\text{v}\) は蒸発エンタルピー \(\Delta \bar{H}_\text{m}\) を温度で割った次式で表されます。

\[ \Delta \bar{S}_\text{v} = \bar{S}_\beta - \bar{S}_\alpha = \frac{\Delta \bar{H}_\text{v}}{T} \]

単にエンタルピーを温度で割るだけで良いのは、融解時と同様で物質が蒸発するとき温度は一定に保たれるためです。

一方、物質の蒸発による体積変化 \(\Delta \bar{V}_\text{v}\) は、融解時とは異なり大胆な近似によって温度依存性を明らかにできます。

その近似とは、一般に気体の体積は液体の体積よりも非常に大きく \(\bar{V}_\beta \gg \bar{V}_\alpha\) の関係が成立する状況において

\[ \Delta \bar{V}_\text{v} = \bar{V}_\beta - \bar{V}_\alpha \simeq \bar{V}_\beta ~~~ ( ~ \bar{V}_\beta \gg \bar{V}_\alpha ~ ) \]

といった具合に、気体の体積のみで表現してしまうものです。

当然扱う物質や温度・圧力条件によっても様々ですが、物質が液体から気体に状態変化するときその体積は数百・数千倍にまで膨張します。

つまり大きく見積もっても液相の体積は系全体の1%程度で、式(10)の近似は妥当と言えるのです。

更に気体が理想的に振る舞うと仮定すれば、理想気体の状態方程式から \(\bar{V}_\beta = \frac{RT}{P}\) が言えるので結局…

\[ \Delta \bar{V}_\text{v} \simeq \frac{RT}{P} \]

の関係が近似的に成立するわけです。

続けて、式(9)および式(11)を式(5)に代入後に整理すると次式が得られます。

\[ \begin{gather*} \frac{dP}{dT} = \frac{\Delta \bar{H}_\text{v}}{RT^2} P \\[15pt] \therefore ~ \frac{dP}{P} = \frac{\Delta \bar{H}_\text{v}}{RT^2} dT \end{gather*} \]

両辺積分を実行するにあたって、蒸発エンタルピー \(\Delta \bar{H}_\text{v}\) が一定値を示す温度範囲に限定すると次のように計算ができます。

\[ \begin{gather*} \int_{P'}^P \frac{dP}{P} = \frac{\Delta \bar{H}_\text{v}}{R} \int_{T'}^T \frac{dT}{T^2} \\[15pt] \ln \frac{P}{P'} = - \frac{\Delta \bar{H}_\text{v}}{R} \left( \frac{1}{T} - \frac{1}{T'} \right) \end{gather*} \]

ここで得られた式(13)はクラウジウス-クラペイロンの式と呼ばれています。

また式(13)の両辺指数をとって整理すると気液共存線 ( 蒸気圧曲線 ) が得られます。

\[ P(T) = P' \exp\bigg[ - \frac{\Delta \bar{H}_\text{v}}{R} \left( \frac{1}{T} - \frac{1}{T'} \right) \bigg] \]

固気共存線の導出

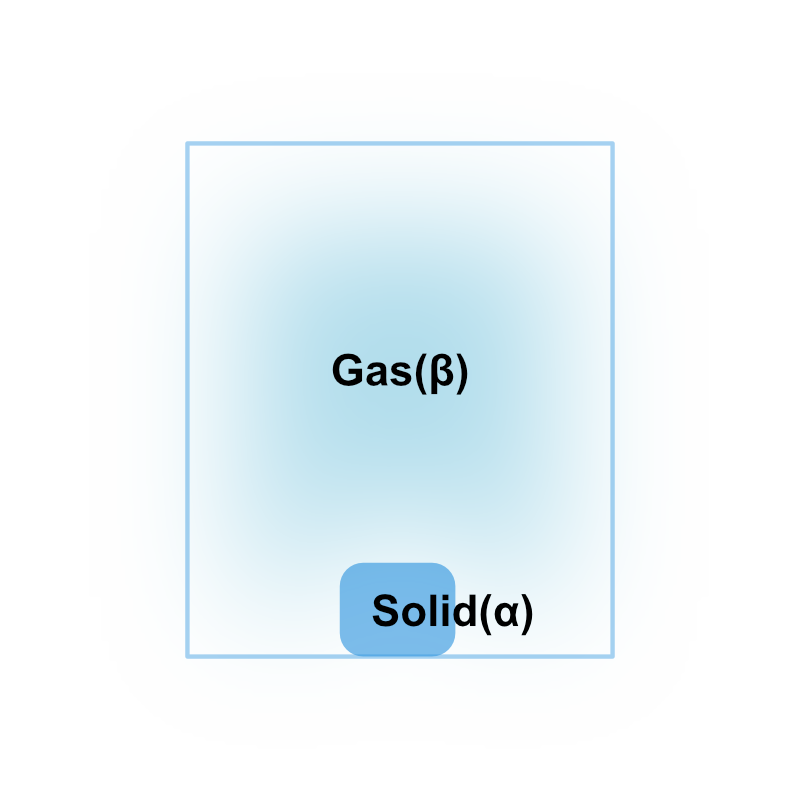
気相と固相が共存する場合について、固気共存線を考えます。

\(\alpha\) 相を固相、\(\beta\) 相を気相であるとすれば、物質の昇華エントロピー \(\Delta \bar{S}_\text{v}\) と昇華による体積変化 \(\Delta \bar{V}_\text{v}\) を求めることになります。

前項までと考える事は全く同じですが、実は気体が関与することから得られる結果は式(13)・式(14)と似ており、蒸発エンタルピーを昇華エンタルピー \(\Delta \bar{H}_\text{s}\) に置き換えたものになります。

\[ \ln \frac{P}{P'} = - \frac{\Delta \bar{H}_\text{s}}{R} \left( \frac{1}{T} - \frac{1}{T'} \right) \]

\[ P(T) = P' \exp\bigg[ - \frac{\Delta \bar{H}_\text{s}}{R} \left( \frac{1}{T} - \frac{1}{T'} \right) \bigg] \]

状態図

ここまでの説明を元に状態図を作成してみましょう。

求めた3つの共存線の概形について、\(\frac{dP}{dT}\) から

\[ \frac{dP}{dT} = \frac{\Delta \bar{H}_\text{m}}{T\Delta \bar{V}_\text{m}} ~~~ ( ~ \Delta \bar{H}_\text{m} > 0 ~ ) \]

\[ \frac{dP}{dT} = \frac{\Delta \bar{H}_\text{v}}{RT^2} > 0 ~~~ ( ~ \because \Delta \bar{H}_\text{v} > 0 ~ ) \]

\[ \frac{dP}{dT} = \frac{\Delta \bar{H}_\text{s}}{RT^2} > 0 ~~~ ( ~ \because \Delta \bar{H}_\text{s} > 0 ~ ) \]

となるように、気液共存線および固気共存線はどちらも単調増加する事が分かります。

一方で固液共存線の傾きは融解に伴うモル体積変化に依存して正負両方の値を取り得ることに注意しなければなりません。

つまり固体状態より液体状態のほうが体積が大きい物質では、固液共存線の傾きが正となり、逆であれば負になるということです。

以上の内容から、単一成分系について一般に次のような状態図が得られます。

3つの共存線はある1点を共有する様に描かれ、この点が前述した「三重点」になります。

三重点では気相・液相・固相の3相が共存した状態を実現できますが、その条件は極めて限定的であり点として表現されることからその名称が与えられているのです。

また3つの共存線によってグラフは3つの領域に区分されていることも分かります。

温度・圧力条件 \((T, P)\) がちょうど曲線上に位置する場合は2相平衡状態となりますが、領域内に位置する場合は気相・液相・固相のいずれか相当する1相のみが存在する状態となります。

状態図を用いれば、温度・圧力条件から系がどのような状態にあるかを一目で判断することができるので非常に便利です。