液体の性質を理解するに当たり、その蒸気に着目することが近道になります。

当ページでは液体の蒸気に焦点を当て、その圧力である蒸気圧について解説を行っていきます。

蒸気圧

蒸気圧とは、液体や固体の一部が状態変化して発生する気体が示す圧力です。

より正確には気液平衡あるいは固気平衝の状態にある物質の気体が示す圧力を指します。

蒸気圧には、下記に示す通り

• 蒸気圧は温度が定まれば一意に決まる
• 蒸気圧は温度上昇に伴い急激に増大する

といった特徴があります。

これらの特徴は熱力学的平衡条件から数学的に理解することが可能です。

以下で順を追って解説を行います。

状態図で見た蒸気圧

系の蒸気圧が定義されるには、当然ながら蒸気の存在が前提となります。

蒸気とは液体や固体が気化して生じる気体であり、気体単体で議論されるものではない事が重要です。

物質が状態を変えるとき、そこには系に加えられた圧力 \(P\) や温度 \(T\)、体積の \(V\) の変化を伴います。

例えば、次に示すのはある純物質の \(P\) - \(V\) 図で、異なる温度条件の下で系が示す挙動を曲線で表しています。

グラフで示す通り、系の体積が大きいと圧力は小さくなる傾向にあります。ところが温度条件によって曲線の概形は全く様子が異なるようです。

高温では滑らかに単調減少する曲線を描いており、物質が概ね理想気体として振る舞うことを表しています。

一方、低温では微分不可能な点 ( 尖点 ) を持つ曲線となり特異的な挙動を示すことが分かります。興味深いのは、体積変化依らず圧力が常に一定値を示す領域が存在することで、この圧力が蒸気圧です。

つまりこの圧力一定領域では気体と液体 ( あるいは固体 ) が共存しており、これより体積が大きい領域では気体のみ、逆に体積が小さい領域では液体 ( あるいは固体 ) のみの状態を取ります。

蒸気圧を記述する関係式

ここでは蒸気圧を記述する関係式を理論的に導いていきます。

何度も言うように、蒸気圧は液体や固体が存在する下で、その蒸気が示す圧力を言います。

蒸気は液体や固体と平衡状態にあるため、それらの化学ポテンシャルが等しい平衡条件が成立する必要があります。

以下、液体とその蒸気が存在する状況、すなわち気液平衡状態を考えることにすると、それぞれの化学ポテンシャル \(\mu^{\text{(L)}}\), \(\mu^{\text{(G)}}\) を用いて

\[ \mu^{\text{(L)}}(T, ~ P) = \mu^{\text{(G)}}(T, ~ P) \]

となります。

詳細の計算方法はクラウジウス-クラペイロンの式を解説したページに譲ることにして、結果のみを示すと蒸気圧 \(P\) は次式のように記述できます。

\[ P = P' \exp \bigg[ -\frac{\Delta H_\text{v}}{R} \left( \frac{1}{T} - \frac{1}{T'} \right) \bigg] \]

• \(P\) : 蒸気圧
• \(T\) : 温度
• \(\Delta H_\text{v}\) : 蒸発エンタルピー
• \(R\) : 気体定数
• \(P'\) : 任意の温度 \(T'\) における蒸気圧

式(2)は蒸気圧曲線 ( 気液共存線 ) と呼ばれ、温度に対して蒸気圧が単調に増加する傾向を示します。

また温度を定めれば蒸気圧は一意に決まることも分かります。

蒸気圧の測定

蒸気圧の測定について触れておきます。

下図に示すような、水銀圧力計が付いた容器を利用します。

はじめ体積 \(V\) の容器内には空気が入っており大気圧 \(P_0\) を示しています。

そこに測定対象の液体を入れて静置させると、液体の一部が気化して蒸気が発生し気相の圧力が増加します。

すると圧力計の水銀の両端に高低差 \(\Delta h\) が生じ、この差から蒸気圧が求められるという仕組みです。

水銀の密度を \(\rho\)、重力加速度を \(g\) として、蒸気圧 \(P\) は次式で与えられます。

\[ P = \rho g \Delta h \]

ただしこの蒸気の測定法は簡易的であり、厳密ではない事に注意する必要があります。

実際に容器には測定対象の物質以外にも空気が含まれています。

気液平衡状態にある純物質Aが入った容器に空気を混合させていった場合、Aの蒸気圧に変化が生じるか計算してみましょう。

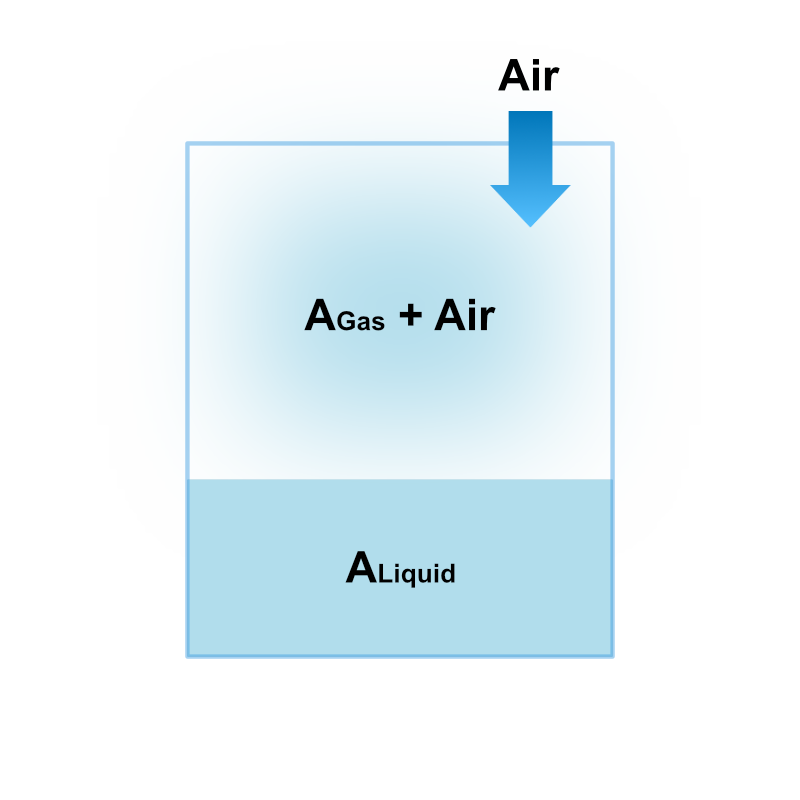
上図で示すように、この多成分系はAのみからなる液相と、Aの蒸気と空気からなる気相で構成されます。

本来空気は僅かに溶解性をもつと言われますが、ここでは簡単のために空気は液体に溶解しないと仮定しました。

多成分系の平衡条件は純物質の場合と同様に化学ポテンシャルのつり合いとして記述でき、異なる物質の間で独立に扱えることから物質Aに対して

\[ \mu_\text{A}^{\text{(L)}}(T, ~ P) = \mu_\text{A}^{\text{(G)}}(T, ~ P; ~ \boldsymbol{n}^{\text{(G)}}) \]

の関係が成立します。ここで \(P\) は空気とAの蒸気による全圧です。

式中の \(\boldsymbol{n}^{\text{(G)}}\) はAの蒸気と空気の物質量の組 \((n_\text{A}, ~ n_\text{air})\) を表しています。

また混合気体の成分の化学ポテンシャルはその分圧 \(P_\text{A}\) を用いて次式で記述できます。

\[ \mu_\text{A}^{\text{(G)}}(T, ~ P; ~ \boldsymbol{n}^{\text{(G)}}) = \mu_\text{A}^{\text{(G)}}(T, ~ P^\circ) + RT \ln \frac{P_\text{A}}{P^\circ} \]

\(P^\circ\) は標準圧力を表しています。

式(5)から式(4)は次のように書き換えられます。

\[ \mu_\text{A}^{\text{(L)}}(T, ~ P) = \mu_\text{A}^{\text{(G)}}(T, ~ P^\circ) + RT \ln \frac{P_\text{A}}{P^\circ} \]

ここから更に空気を加えていきます。

すると全圧 \(P\) は \(P + dP\) に変化し、同時にAの蒸気の分圧も \(P_\text{A}\) から \(P_\text{A} + dP_\text{A}\) に置き換えます。

\[ \mu_\text{A}^{\text{(L)}}(T, ~ P + dP) = \mu_\text{A}^{\text{(G)}}(T, ~ P^\circ) + RT \ln \frac{P_\text{A} + dP_\text{A}}{P^\circ} \]

以下テイラー展開を利用しながら解析を進めていきます。まずは式(7)左辺についてテイラー1次近似を行うと次のようになります。

\[ \begin{align*} \mu_\text{A}^{\text{(L)}}(T, ~ P + dP) &= \mu_\text{A}^{\text{(L)}}(T, ~ P) + \left( \frac{\partial \mu_\text{A}^{\text{(L)}}}{\partial P} \right)_T dP \\[15pt] &= \mu_\text{A}^{\text{(L)}}(T, ~ P) + \bar{V}_\text{A}^{\text{(L)}} dP \end{align*} \]

式(8)の最後で、次式の化学ポテンシャルの圧力に関する微分係数はモル体積と等しい関係を利用しました。

\[ \left( \frac{\partial \mu_\text{A}^{\text{(L)}}}{\partial P} \right)_T = \bar{V}_\text{A}^{\text{(L)}} \]

続いて式(7)右辺の対数項を変形していきます。

\[ \begin{align*} RT \ln \frac{P_\text{A} + dP_\text{A}}{P^\circ} &= RT \ln \bigg[ \frac{P_\text{A}}{P^\circ} \left( 1 + \frac{dP_\text{A}}{P_\text{A}} \right) \bigg] \\[15pt] &= RT \ln \frac{P_\text{A}}{P^\circ} + \textcolor{red}{RT \ln \left( 1 + \frac{dP_\text{A}}{P_\text{A}} \right)} \end{align*} \]

式(10)の赤色で示した項について、\(\ln (1 + x) \simeq x\) の近似が利用できます。

\[ RT \ln \left( 1 + \frac{dP_\text{A}}{P_\text{A}} \right) \simeq RT \frac{dP_\text{A}}{P_\text{A}} \]

以上をまとめると、結局式(7)は近似によって次のように整理できることが分かります。

\[ \mu_\text{A}^{\text{(L)}}(T, ~ P) + \bar{V}_\text{A}^{\text{(L)}} dP = \mu_\text{A}^{\text{(G)}}(T, ~ P^\circ) + RT \ln \frac{P_\text{A}}{P^\circ} + RT \frac{dP_\text{A}}{P_\text{A}} \]

式(12)から式(6)を差し引くと次式が得られます。

\[ \bar{V}_\text{A}^{\text{(L)}} dP = RT \frac{dP_\text{A}}{P_\text{A}} \]

両辺、積分を行います。このとき全圧は \([P_\text{init}, ~ P]\)、Aの蒸気の分圧は \([P_\text{Ainit}, P_\text{A}]\) で変化させるとして

\[ \int_{P_\text{init}}^P \bar{V}_\text{A}^{\text{(L)}} dP = RT \int_{P_\text{Ainit}}^{P_\text{A}} \frac{dP_\text{A}}{P_\text{A}} \]

一般に液体のモル体積は圧力によって大きく変化しないとして、\(\bar{V}_\text{A}^{\text{(L)}}\) を定数と見なせば

\[ \begin{align*} &\bar{V}_\text{A}^{\text{(L)}} (P - P_\text{init}) = RT \ln \frac{P_\text{A}}{P_\text{Ainit}} \\[15pt] \Leftrightarrow ~ & P_\text{A} = P_\text{Ainit} \exp \bigg[ \frac{\bar{V}_\text{A}^{\text{(L)}} (P - P_\text{init})}{RT} \bigg] \end{align*} \]

が得られます。

またAの蒸気が理想的に振る舞うとして、理想気体の状態方程式からモル体積は

\[ \bar{V}_\text{A}^{\text{(G)}} = \frac{RT}{P_\text{Ainit}} \]

で与えられるので、式(15)と式(16)から \(RT\) を消去すると次の式が導かれます。

\[ P_\text{A} = P_\text{Ainit} \exp \bigg[ \frac{\bar{V}_\text{A}^{\text{(L)}}}{\bar{V}_\text{A}^{\text{(G)}}} \frac{P - P_\text{init}}{P_\text{Ainit}} \bigg] \]

さてこの結果から、蒸気圧測定を行う上で空気の存在があまり影響を及ぼさない事を理解することができます。

着目したいのは指数項のモル体積 \(\bar{V}_\text{A}^{\text{(L)}}\), \(\bar{V}_\text{A}^{\text{(G)}}\) で、当然扱う物質にも依りますが気体のモル体積の方が約1000倍近く大きくモル体積の比 \(\frac{\bar{V}_\text{A}^{\text{(L)}}}{\bar{V}_\text{A}^{\text{(G)}}}\) は非常に小さい値を示します。

つまり指数項をほぼ 1 として見なせるため、空気が存在していたとしても測定で得られる蒸気圧に大きな誤差が生じないということです。

とは言え、式(17)を導くにあたって設けた幾つかの仮定が破綻していれば、この結論は成立しないため注意する必要はあるでしょう。