関数を解析する際には、何気なく微分することがあるかもしれません。

しかしながら実際には微分を実行する前にその関数が本当に微分可能であるのかを考えなければなりません。

当コンテンツでは、その微分可能性が一体何を表すのかを再度確認し、その上で多変数関数に応用していきます。

更にその結果得られる「全微分」と呼ばれる関係から、いくつかの重要な微分公式を導きます。

多変数関数の微分可能性

微分可能性の復習

考える定義域内で、途中で途切れていたり、とがった点を持たない関数 \(f(x)\) を考えます。

このとき \(f(x)\) は定義域全域で微分可能であると言い、数学的には次の関係を利用して判定することができます。

\[ \lim_{x \rightarrow a + 0} \frac{f(x) - f(a)}{x - a} = \lim_{x \rightarrow a - 0} \frac{f(x) - f(a)}{x - a} \]

つまり点 \(x = a\) を中心にほんの少し左右に移動した地点においてもグラフの傾きは等しいことを表しています。

逆に、微分可能でない場合はこの関係が成立しません。

例えば次の図に示すような \(x = 0\) でとがった点を持つ次のグラフは \(x = 0\) を中心にほんの少し左右に移動した地点でのグラフの傾きは異なります。

また、関数の一部分において微分不可能であるからと言って、関数全体が微分不可能になる訳ではありません。微分不可能な点を避けて考えれば、微分を実行することが可能です。

以上が微分可能性の概要になりますが、要するにグラフが途切れていたり、とがっていたりすること無く、滑らかに繋がっているグラフであれば微分可能であると理解しておけば問題ありません。

次の項では以上の内容を踏まえて多変数関数に応用していくことを考えましょう。

多変数関数の微分可能性

前項で示した内容を参考に多変数関数についての微分可能性を考えていきましょう。

ところがそのまま多変数関数に応用しようとしても、一体どのようにすればいいのか疑問が生じてしまいます。

実際、1変数関数では微分を実行したい点 \(x = a\) からほんの少し移動した点である \(x = a + 0\) および \(x = a - 0\) を調査すれば事が足りましたが、多変数関数ではそうはいきません。

その事を説明するために、以下2変数関数を考えることにしましょう。

2変数関数のグラフは3次元空間中に曲面として広がることは別のコンテンツで示したとおりです。

するとある地点において微分可能であるためには、その点周辺において滑らかにグラフが広がっている必要があるということになります。

つまり1変数関数の場合は、判定したい点を中心に \(x\) 軸方向だけを考えればよかったところ、2変数関数では360°の方向を考えなければならないのです。

これを数学的にアプローチしていくことも可能ですが、もう少し簡単になるように話を展開してみます。

1変数関数の場合の微分可能性を図形的に捉えてみましょう。

結論から言ってしまうと、1変数関数が微分可能であるとは、グラフの一部分を拡大すると直線として表現することが可能であることを言います。

この一部分とは、すなわち微分可能であるかを判定したい点周辺のことです。

次に曲線の一部分を拡大した図を示していますが、「ほぼ直線」に見えることが分かります。

本題である多変数関数について話を戻します。同様に多変数関数も一部分を拡大してみるとどのようになるのか見てみましょう。

グラフの一部分を拡大してみると、多少の歪んで見えるものの、ほとんど平面に見えることが分かります。

1変数関数が微分可能であるときに接線を引けたように、実は2変数関数について微分可能であるならば、曲面に接する平面、すなわち接平面を張ることができるのです。

次の節以降でこの接平面の方程式を導出していきます。

平面の方程式

まず初めとして、平面を数学的に表現する方法を知る必要があります。

平面の方程式を導くための準備として、平面の一部分を含んだ3辺の長さが \(\Delta x\), \(\Delta y\), \(\Delta z\) の直方体を考えましょう。

点Aの座標は定数を用いて(\(a, ~ b, ~c\))とし、点Bの座標は変数を用いて (\(x, ~ y, ~ z\))としておきます。

また、点Bは点Aからそれぞれ3軸方向に \(\Delta x\), \(\Delta y\), \(\Delta z\) だけ動いた点であるから、B(\(a + \Delta x, ~ b + \Delta y, ~ c + \Delta z\))と表現することができます。

つまり、\(\Delta x = x - a\), \(\Delta y = y - b\), \(\Delta z = z - c\) という関係が成立していることになります。

それから \(\Delta z\) を図に示すように \(\Delta z_1\) と \(\Delta z_2\) に分割して考えてみましょう。

式(1)

\[ \Delta z = \Delta z_1 + \Delta z_2 \]

式(1)に示す通り点Aから点Bへ移動した際の \(z\) 座標の変化量 \(\Delta z\) は、点Aから点Cへ \(x\) 軸方向に移動したときの \(z\) 座標の変化量 \(\Delta z_1\) と、続けて点Cから点Bへ \(y\) 軸方向に移動した際の \(z\) 座標の変化量 \(\Delta z_2\) の足し算で表現することができます。

また点Aから \(x\) 軸方向に \(\Delta x\) だけ移動したときに \(\Delta z_1\) だけ \(z\) 座標が変化することから、この平面の \(x\) 軸方向の傾き \(\left(\frac{\partial z}{\partial x}\right)_y\) が \(\frac{\Delta z_1}{\Delta x}\) であることが分かります。

同様に平面の \(y\) 軸方向の傾き \(\left(\frac{\partial z}{\partial y}\right)_x\) は \(\frac{\Delta z_2}{\Delta y}\) と表せるわけですね。

したがって \(\Delta z_1\) および \(\Delta z_2\) は \(x\), \(y\), \(z\) を用いて次のように書けることになります。

式(2)

\[ \left\{ \begin{align*} ~ \left(\frac{\partial z}{\partial x}\right)_y = \frac{\Delta z_1}{\Delta x} \\[20pt] ~ \left(\frac{\partial z}{\partial y}\right)_x = \frac{\Delta z_2}{\Delta y} \end{align*} \right. ~ \Leftrightarrow ~ \left\{ \begin{align*} ~ \Delta z_1 = \left(\frac{\partial z}{\partial x}\right)_y \Delta x \\[20pt] ~ \Delta z_2 = \left(\frac{\partial z}{\partial y}\right)_x \Delta y \end{align*} \right. \]

式(1)および式(2)から、\(\Delta z_1\), \(\Delta z_2\) を消去すると次式が得られます。

式(3)

\[ \begin{align*} & \Delta z = \left(\frac{\partial z}{\partial x}\right)_y \Delta x + \left(\frac{\partial z}{\partial y}\right)_x \Delta y \\[20pt] \Leftrightarrow ~ & z - c = \left(\frac{\partial z}{\partial x}\right)_y (x - a) + \left(\frac{\partial z}{\partial y}\right)_x (y - b) \end{align*} \]

幾何学的に導かれたこの式(3)こそが求めていた平面の方程式です。

偏微分を用いて表現しなくても、一般的に \(x\) と \(y\) の1次式の和であることが本質なので

\[ z = A (x - a) + B (y - b) + C \]

と簡単に表現をされることもあります。

全微分

接平面の方程式

準備が整ったので、本題である接平面の方程式を導いてみましょう。

と言っても行うことはたった一つなので身構える必要はありません。

順を追って説明したいため、1変数関数の場合に相当する接線がどのように得られたのか再度確認しておきましょう。

※詳細は「微分法の基礎」で説明しているので参照してください。

次の図は1変数関数 \(f(x)\) 上に2点A, Bを取って間隔を狭くしていく場面を表しています。

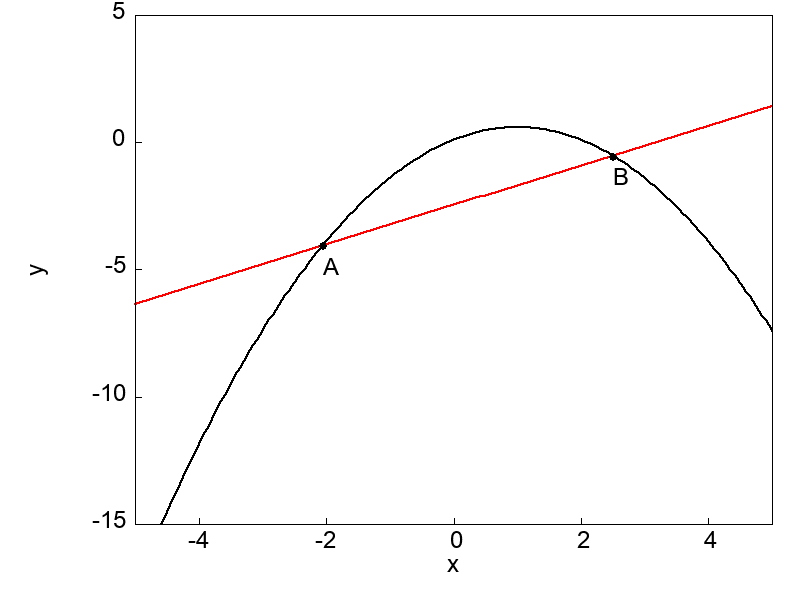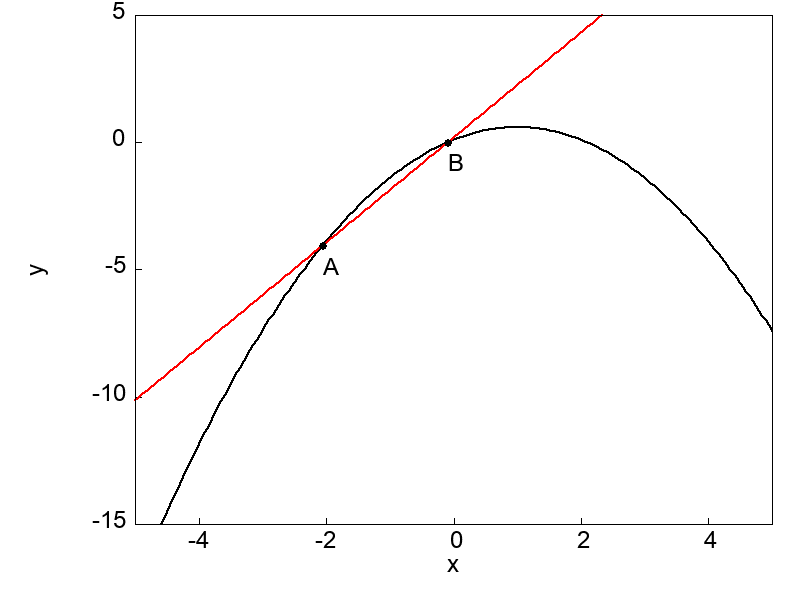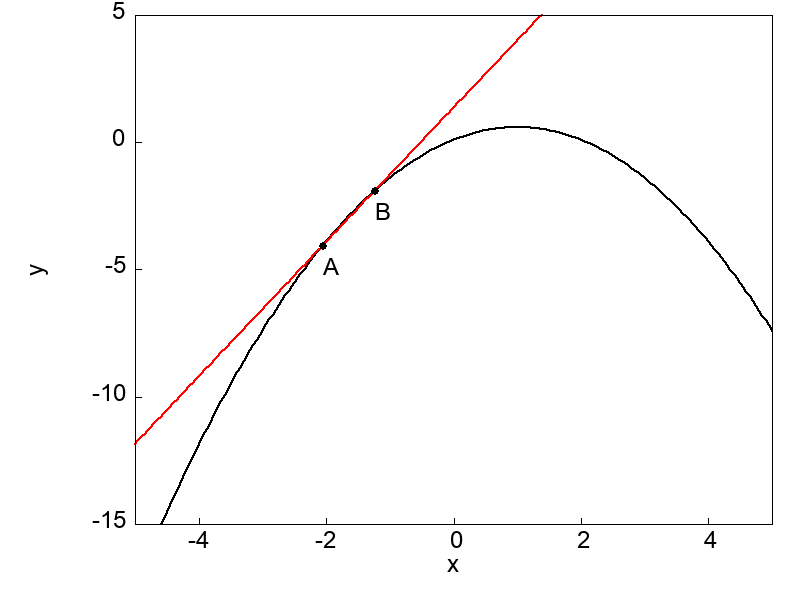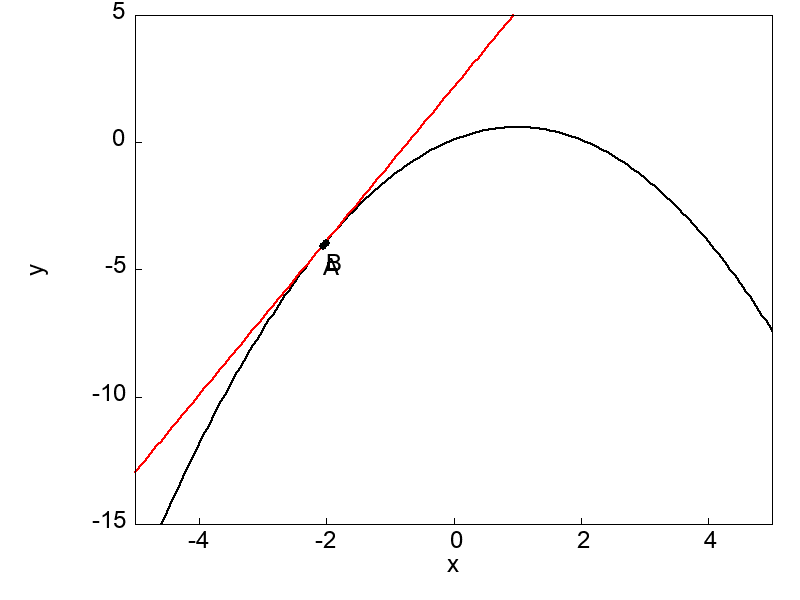
点Aと点Bが近づいていくのに伴って、2点を通る直線は段々と曲線の接線に近づいていきます。

この考え方を拡張して、曲面上での微分操作を考えていきます。

次の図に示すように曲面 \(f(x, ~ y)\) 上に2つの点A(\(a, ~ b, ~ c\))およびB(\(x, ~ y, ~ z\)) を取りましょう。

加えて、点Aおよび点Bを含む平面も合わせて描画しています。

現状では平面が曲面の一部を貫通してしまっていますが、固定された点Aに点Bを近づける極限操作を行うことによって曲面に接する平面、すなわち接平面が得られます。

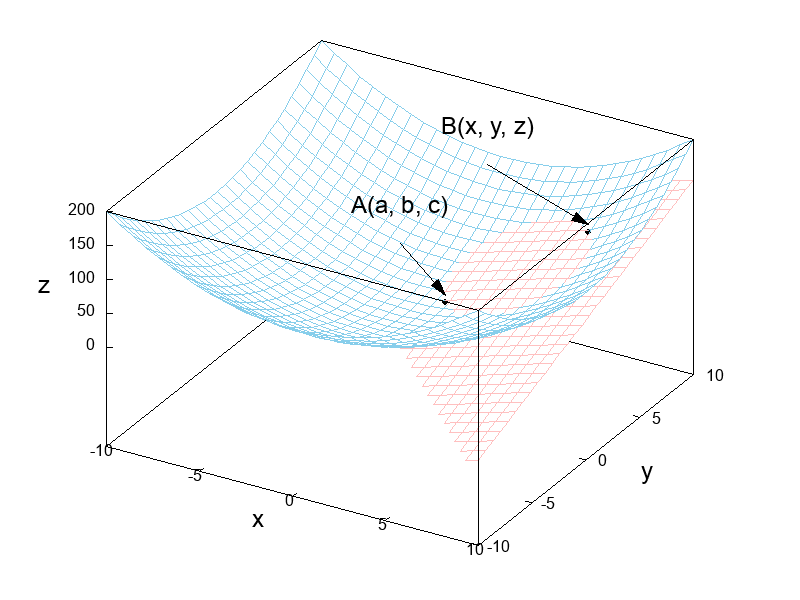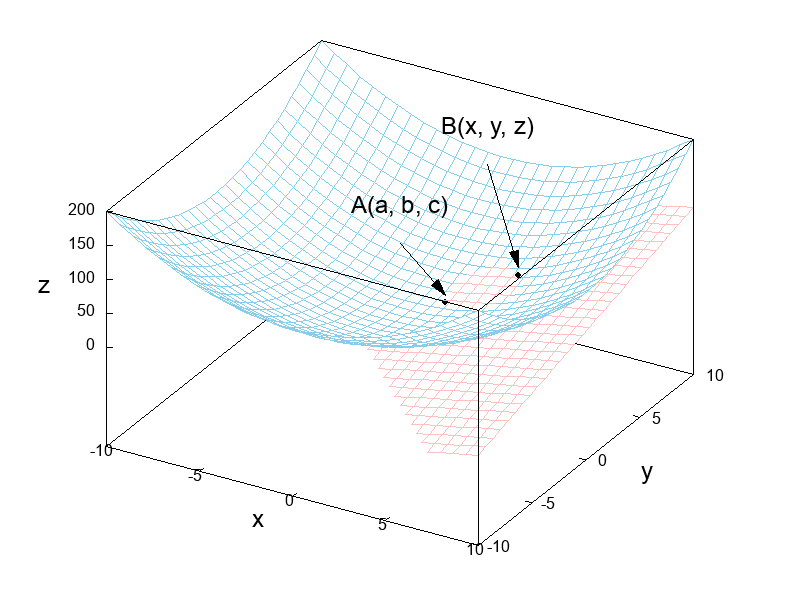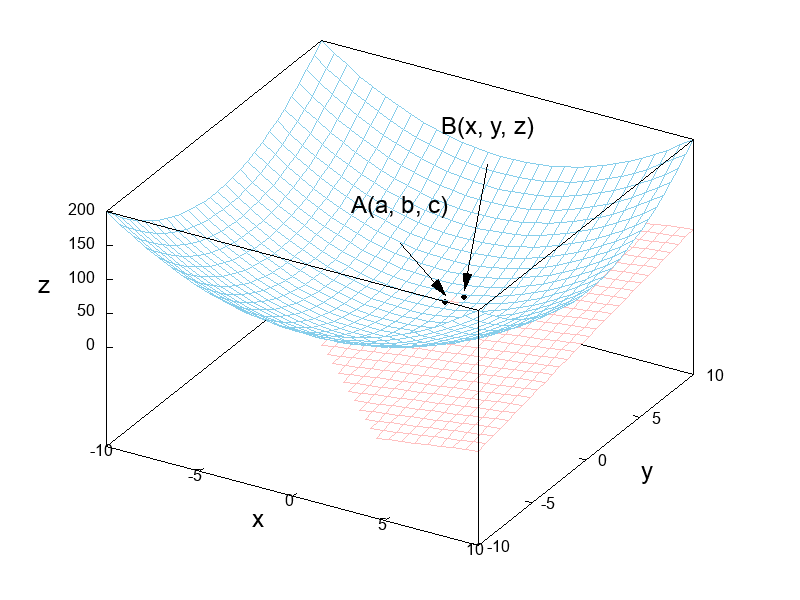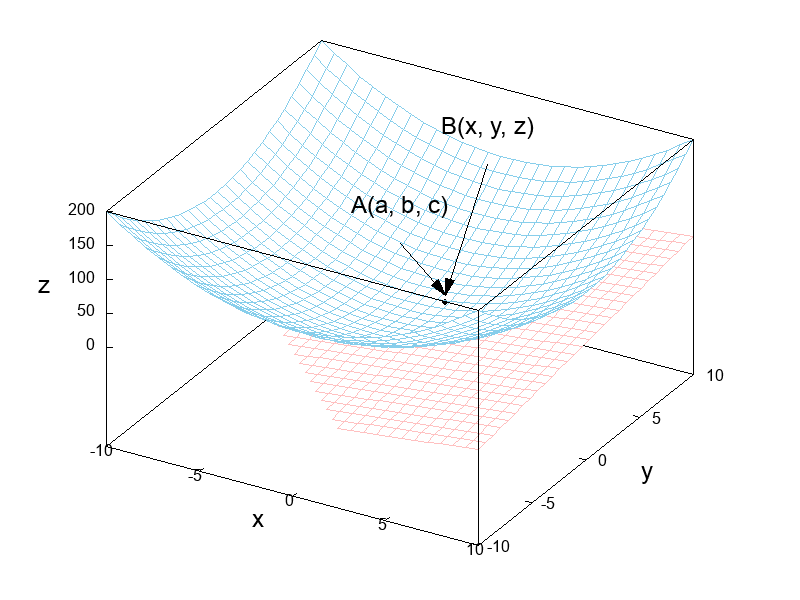
また重要なことは、ただ一つの接平面が得られることであり、これは1変数関数が微分可能であるときに接線が1つだけ引けることと同様です。

以上の内容を踏まえると接平面の方程式は簡単に得ることができます。まずは結果を示すことにしましょう。

式(4)

\[ dz = \left(\frac{\partial z}{\partial x}\right)_y dx + \left(\frac{\partial z}{\partial y}\right)_x dy \]

式(4)は式(3)の変化量 \(\Delta x\), \(\Delta y\), \(\Delta z\) をそれぞれ微小量 \(dx\), \(dy\), \(dz\) に置き換えただけです。

※微小量については「微分法の基礎」を参照してください。

前節で曲面の一部分を限りなく拡大したときに平面として見ることができることと、限りなく近づいた結果観測できるスケールはとても小さくなるので微小量で表現できることを合わせれば納得していただけることでしょう。

よってこれまでの内容を整理すると、2変数関数がある点について微分可能であるとき、その点における接平面がただ1つ存在するとまとめることができます。

また2変数以上の多変数関数が微分可能であるとき、特別に全微分可能と言うので覚えておきましょう。

全微分不可能な場合

逆に全微分が不可能な場合はどうでしょうか。

筆者の拙い説明でもここまでの内容を理解していただければ、次に示す関数 \(z = \sqrt{|xy|}\) は全微分不可能であることが分かるでしょう。

この関数は \((x, ~ y) = (0, ~ 0)\) の地点でとがった点を持ちます。

全微分不可能である理由は、この点においてただ1つの接平面を定めることができない為というのは、当コンテンツ冒頭で示した1変数関数の場合の類推から理解できるでしょう。

では、続いて次の関数 \(z = \frac{x^2 y}{x^2 + y^2}\) のグラフを見ていただきましょう。

実はこちらも \((x, ~ y) = (0, ~ 0)\) 全微分不可能な関数です。

この類の関数を例にあげられることは多いのですが、筆者自身は感覚的にどうも納得いかず困り果てた事あります。

「この点周りで拡大していくと平面に近づくのではないか？」という疑問がずっと残っていたからです（その思考のプロセスに需要があれば示します）。

それならと、実際に好きなだけ拡大してみればどうなるのか確認してみた結果が次の図です。

スケールを確認していただければお分かりかと思いますが、はじめの状態から10000倍に拡大しています。

それにも関わらず拡大前と全く同じ形状のグラフであることに驚くでしょうか。

限りなく拡大したところで平面に近づくことが無いため、一旦この関数が全微分不可能であることは認めるとしても、次には「なぜ拡大しても平面化しないのか？」という疑問が生じます。

この疑問を解決するためことは非常に簡単で、数学的にグラフの拡大操作を実行すれば良いだけです。

グラフの拡大は、関数に含まれる \(x\), \(y\), \(z\) をそれぞれ \(\epsilon x\), \(\epsilon y\), \(\epsilon z\) で置き換えることによって表現できます。

要するに \(\epsilon\) は倍率を表していて、現に \(\epsilon = 0.0001\) にすると先程のグラフが得られます。

その計算過程を以下に示しました。

\[ \begin{align*} z = \frac{x^2 y}{x^2 + y^2} ~ \xrightarrow{~~~ \text{Expansion} ~~~} & ~ \epsilon z = \frac{(\epsilon x)^2 \epsilon y}{(\epsilon x)^2 + (\epsilon y)^2} \\[20pt] \Leftrightarrow & ~ \epsilon z = \frac{\epsilon ^3 x^2 y}{\epsilon^2 (x^2 + y^2)} = \epsilon \frac{x^2 y}{x^2 + y^2} \\[20pt] \Leftrightarrow & ~ z = \frac{x^2 y}{x^2 + y^2} \end{align*} \]

このように、両辺で \(\epsilon\) がキャンセルされ元通りに戻ってしまうために、いくら拡大してもグラフの形状に変化がないのです。

※拡大すると平面化する関数では \(\epsilon\) がキャンセルされず残ります。冒頭で紹介した下に凸の曲面は \(z = x^2 + y^2\) で表現されます。実際に拡大操作を施すと、\(z = \epsilon (x^2 + y^2)\) となります。