熱力学系に対して外から力学的操作を行ったとき、どのような応答を示すのかによって系の状態を理解することができます。

外から系を眺めているだけではなく、実際に触れることで初めて理解できることも多分にあるということです。

当ページでは基本的な操作の記述について解説した後、具体的に等温操作と断熱操作を取り上げていきます。

力学的操作

私達が熱力学系がもつ情報を得ようとしたとき、力学的操作が重要な役割を果たします。

ここでいう「系がもつ情報」とは、例えば次に示すような熱平衡状態が1つです。

\[ (T; ~ V, ~ n) \]

系の平衡状態を特定するには内部の温度 \(T\)、体積 \(V\)、物質量 \(n\) を定めることによって求めることができます。

ただ、系から得られる情報はこれで全てではありません。

外から系を観察するだけでなく、実際に触ってみることが重要です。

それが系に対する力学的操作になります。

力学的操作とは、多くは系の示量変数を変化させることを意味します。

例えば、流体が封入されたピストン付きの容器を考えたとき、ピストンを操作して体積 \(V\) を変化させたりします。

以降、系をある平衡状態 \((T_1; ~ V_1, ~ n_1)\) から別の平衡状態 \((T_2; ~ V_2, ~ n_2)\) 変化させたり、或いは変化したりするとき次のように記述することにします。

\[ (T_1; ~ V_1, ~ n_1) ~ \rightarrow ~ (T_2; ~ V_2, ~ n_2) \]

ちなみに、上記の記述方法は『熱力学 現代的な視点から（新物理学シリーズ）田崎晴明 著』を参考にしています。

「物理化学」の書籍では、余り見かける記述ではないですが、系の状態を細かく追うことができ更に数学的処理をする際の思考の整理にも最適なのでオススメです。

内容自体は中級者向けとなっていますが、私自身"この記述のおかげ"で熱力学の理解が遥かに向上したと言っても良いです。

広告

等温操作と断熱操作

ここからは具体的な操作の紹介に移ります。

主に等温条件下で行う等温操作と、断熱条件下で行う断熱操作が重要です。

• 等温操作 : 等温環境下に置かれた系に対して外からする力学的操作
• 断熱操作 : 断熱された系に対して外からする力学的操作

それ以前に、等温条件と断熱条件の違いについて理解があやしい方は、こちらに解説ページを設けていますので参照ください。

それぞれの操作でどういった特徴があるのか、パートに分けて説明していきます。

等温操作

等温操作とは等温環境に置かれた系に対して外から仕事をすることを言います。

いま \(n ~ [\text{mol}]\) の気体が封入された容器が温度 \(T ~ [\text{K}]\) の等温環境下に置かれているとします。

この条件の下、系に外から仕事をして容積を \(V ~ [\text{m}^3]\) から \(V'\) に変化させる状況を考えましょう。

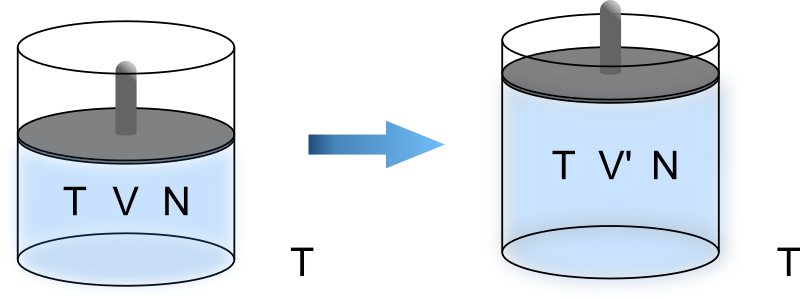
このとき系は、初期の平衡状態 \((T; ~ V, ~ n)\) から別の平衡状態 \((T; ~ V', ~ n)\) に変化するので、

\[ (T; ~ V, ~ n) ~ \xrightarrow{\text{i}} ~ (T; ~ V', ~ n) \]

と書けます。

"等温"操作なので、操作前後の温度は互いに同じです。

また操作(1)矢印上部の「 i 」は "等温" を英語で表した "isothermal" の頭文字を表しています。

ただし等温操作について理解しておくべき事項があります。

それは、操作の途中においても系の内部温度が一定であることを問わない点です。

これは系に対して外から仕事を行うとき、必ず非平衡状態を経由することに由来します。

非平衡状態ではこちらで説明したとおり系全体が均一になっておらず、各所で様々な温度をとる可能性があるのでした。

最終的には外部環境との熱のやり取りによって系の温度は \(T\) になります。

※等温操作について更に詳細な内容は、以下のページでより詳しく解説しているので参考にしてください。

断熱操作

断熱操作とは断熱された系に対して外から仕事をすることを言います。

いま \(n ~ [\text{mol}]\) の気体が封入された断熱容器を考えます。

断熱壁に小さな穴を開け、内部に影響を与えないように静かに温度計を差し込んだとき目盛りは \(T ~ [\text{K}]\) を指していたとします。

では断熱条件下で系の容積を \(V ~ [\text{m}^3]\) から \(V'\) に変化させる状況を考えましょう。

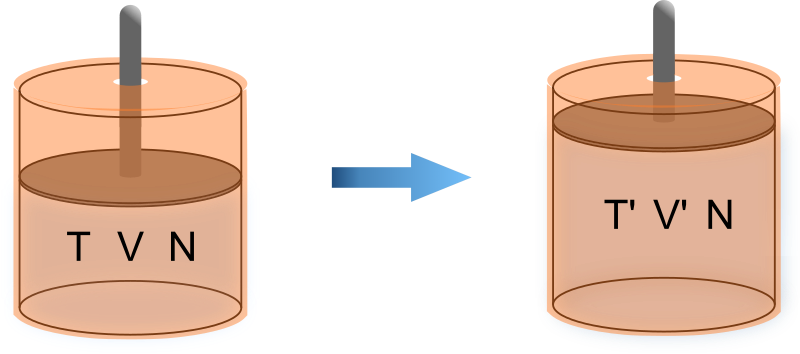
このとき系は、初期の平衡状態 \((T; ~ V, ~ n)\) から別の平衡状態 \((T'; ~ V', ~ n)\) に変化します。

そして上記の断熱操作を、等温操作と同様に記号を用いて次のように表現することにしましょう。

\[ (T; ~ V, ~ n) ~ \xrightarrow{\text{a}} ~ (T'; ~ V', ~ n) \]

操作(2)矢印上部の「 a 」は "断熱" を英語で表した "adiabatic" の頭文字を表しています。

断熱操作では、等温操作とは異なり系の温度は操作前後で変化します。

また操作後の温度 \(T'\) の大きさは完全に系によって決定され、私達が任意の温度にすることはできません。

操作前後で温度が異なるのは、系が外部環境と熱のやり取りをできないためです。

何度も言うように、系に力を加えると非平衡状態となりあらゆる箇所で温度ムラを生じますが、等温環境下であれば系は外部環境と熱のやり取りをし、最終的に外部環境と同じ温度に落ち着きます。

ところが断熱条件ではそうではなく、外からの仕事による影響が温度変化として残ってしまうのです。

※断熱操作について更に詳細な内容は、以下のページでより詳しく解説しているので参考にしてください。

補足 ( 定圧・定積過程について )

系の操作について等温操作と断熱操作を取り上げましたが、それ以外にも系の体積を一定にした過程 ( 定積過程 ) や、系に加わる圧力を一定にした過程 ( 定圧過程 ) などがあります。

ところが定積過程や定圧過程では、外からの力学的な操作を加えることは基本的にはありません。

定積過程については、そもそも体積一定であるため外からの仕事による体積変化を考えることはできません。これは問題なく納得して頂けると思います。

次に定圧過程についてですが、こちらは詳しく解説しましょう。

多くの場合、系に加わる圧力を一定にするためにおもりをピストン上に乗せるなどの方法をとります。

おもりの質量が \(m ~ [\text{g}]\) で、ピストンの断面積を \(S ~ [\text{m}^2]\) とすれば、一定圧力 \(\frac{mg}{S} ~ [\text{Pa}]\) を系に加えることができます。

ではこの状態からピストンを操作するとどうなるでしょうか。おもりから加わる力以外に外から操作するための力も加わりますので、当然圧力は変化してしまいますよね。

したがって定圧過程では、圧力一定という条件を満たすために外から力学的操作を行うことは普通考えないのです。

一般に定圧条件においては、系の温度を変化させて体積に変化を与えます。気体を温めれば膨張し、冷却すれば縮小するといった具合です。

とは言え、体積一定もしくは圧力一定の条件の下でも外から力学的な操作をすることが不可能だということではありません。

例えば系に撹拌翼を挿入しておいて、外から操作して中で撹拌するという操作ができます。

この方法は示量変数を直接変化させるものではありませんが、実際の実験においてはよく利用されます。

また当サイトでも「ジュールの法則」について解説する際にこの方法が現れます。

まとめ

熱力学系がもつ情報を知るには、系に力学的操作をする必要があります。

力学的操作とは、主に系の示量変数である体積 \(V\) を変化させることを指します。

系を操作して、ある平衡状態 \((T_1; ~ V_1, ~ n_1)\) から別の平衡状態 \((T_2; ~ V_2, ~ n_2)\) に変化させるとき次のように表現します。

\[ (T_1; ~ V_1, ~ n_1) ~ \rightarrow ~ (T_2; ~ V_2, ~ n_2) \]

熱力学では、等温操作 ( 等温条件下における操作 ) と断熱操作 ( 断熱条件下における操作 ) が重要です。

閉鎖系の体積を \(V\) から \(V'\) に変化させた場合、それぞれを次のように表記します。

\[ (T; ~ V, ~ n) ~ \xrightarrow{\text{i}} ~ (T; ~ V', ~ n) \]

\[ (T; ~ V, ~ n) ~ \xrightarrow{\text{a}} ~ (T'; ~ V', ~ n) \]

矢印上部の「 i 」および「 a 」はそれぞれ "等温 : isothermal"、"断熱 : adiabatic" の頭文字です。

また最も着目すべき点は操作前後における温度の様子であり、等温操作は前後で変化しませんが、断熱操作では前後で変化します。