熱力学系の状態は平衡状態にあるときのみ記述することが可能ですが、そもそも平衡状態とは熱力学的にどのように記述できるのでしょうか。

当ページではエントロピーの法則を利用して、熱平衡状態にある熱力学系に成立する熱力学的関係式を導出していきます。

温度のつり合い

温度 \(t_\text{high}\) の高温物体と温度 \(t_\text{low}\) の低温物体を接触させると境界では \(\Delta t = t_\text{high} - t_\text{low}\) 温度差が生じ、結果として高温物体から低温物体への熱移動が起こります。

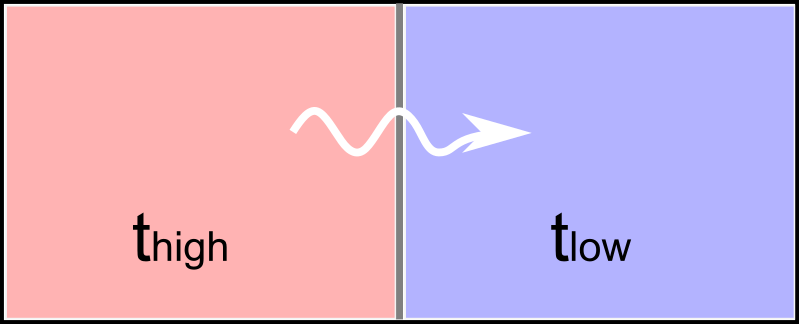
熱移動によってそれぞれの物体は \(t_\text{high}\) と \(t_\text{low}\) のちょうど中央くらいの温度に落ち着くように変化し、最終的にいわゆる平衡状態へと到達します。

私達はその平衡状態において経験的にそれぞれの物体が同じ温度になる事を知ってはいますが、理論的にはどの様な仕組みに支配されているでしょうか。

異なる温度の物体を接触させて温度が均一化された物体は、元あったようなそれぞれ異なる温度を持った状態に自然に戻ることは決してありません。

系はその時々で最適な状態を選ぶように状態を変化させますが、これはまさしくエントロピーの作用によるものです。

そこでエントロピー増大の法則を利用し、平衝状態はどのように理解できるのかを以下で見ていきましょう。

次に示すような部屋1と部屋2に仕切られた容器を考えます。

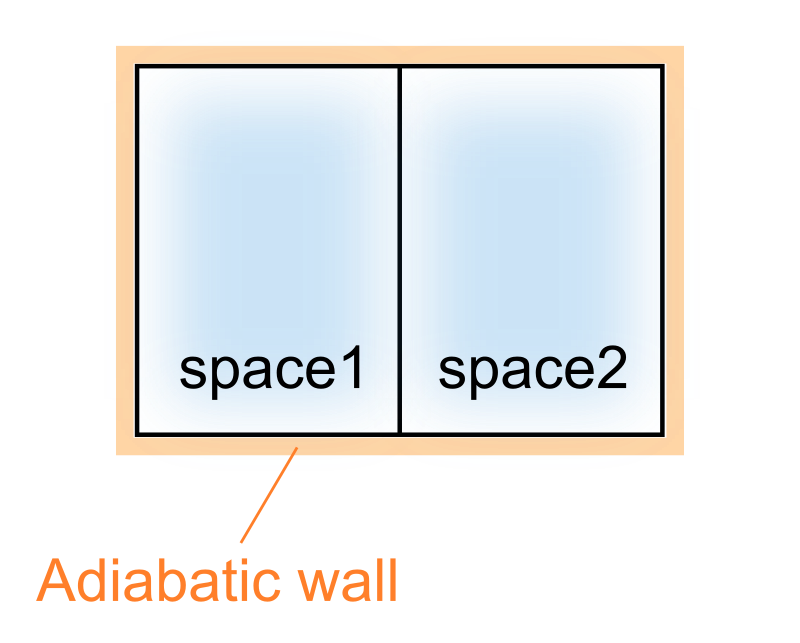
それぞれの部屋は全く同じ気体が封入されています。

また中間に挟まれた仕切りはしっかりと固定されており、それぞれの部屋の体積が変化することはありません。

更に容器全体は断熱壁で完全に覆ってしまいます。こうする事で次に示すエントロピー増大の法則が利用できるようになります。

\[ S_\text{init} \leq S_\text{fin} \]

添字のinitは始状態、finは終状態を表しています。

式(1)について、等号は始状態から終状態への変化が可逆的であるときに成立し、他方で不可逆的であるときには必ずエントロピーは大きくなる事を意味します。

系が平衡状態にあるとき、ある瞬間と次の瞬間の状態は等しいと言えます。

しかし、例えば部屋が温度一定になるように空調を設定していたとしても温度計の指示値が多少揺らぐのと同じ様に、平衡状態とは言え 見かけ上 変化が認められない程度の状態の揺らぎがあると考えられます。

要するにその程度の揺らぎであれば元の状態に戻れる、すなわち可逆過程として扱えるということです。

先の断熱容器が平衡状態にあるとき、2つの部屋の温度がそれぞれ \(T_1\), \(T_2\) にあるとします。

各部屋の温度が \(\delta T_1\), \(\delta T_2\) だけ揺らぐとして、状態が揺らぐ前後における系のエントロピーの関係は次の通りに表すことができます。

\[ S\big( (T_1; ~ V_1, ~ n_1), ~ (T_2; ~ V_2, ~ n_2) \big) = S\big( (T_1 + \delta T_1; ~ V_1, ~ n_1), ~ (T_2 + \delta T_2; ~ V_2, ~ n_2) \big) \]

※ここで \(\delta\) は微分を表す \(d\) と表面的には同じ様に扱える程度に理解しておけば問題ありません。違いは \(d\) は実際の微小変量であるのに対し、\(\delta\) は仮想的な変量という点です。

複合系はそれぞれの部分系の状態量の和に分解できるので、式(2)の両辺は次のように書き換えることができます。

\[ S_1(T_1; ~ V_1, ~ n_1) + S_2(T_2; ~ V_2, ~ n_2) = S_1(T_1 + \delta T_1; ~ V_1, ~ n_1) + S_2(T_2 + \delta T_2; ~ V_2, ~ n_2) \]

式(3)右辺をテイラー1次近似で展開すると

\[ \begin{align*} S_1(T_1 + \delta T_1; ~ V_1, ~ n_1) = S_1(T_1; ~ V_1, ~ n_1) + \left(\frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial T}\right)_{V, ~ n} \delta T_1 \\[20pt] S_2(T_2 + \delta T_2; ~ V_2, ~ n_2) = S_2(T_2; ~ V_2, ~ n_2) + \left(\frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial T}\right)_{V, ~ n} \delta T_2 \end{align*} \]

であるから、結局 式(3)は次のように整理されます。

\[ \left(\frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial T}\right)_{V, ~ n} \delta T_1 + \left(\frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial T}\right)_{V, ~ n} \delta T_2 = 0 \]

ここでエントロピーの温度に関する偏微分係数は、体積と物質量を固定する条件の下で次の関係が成り立ちます。( ※詳しくはエントロピーの解説ページへ。)

\[ \left( \frac{\partial S}{\partial T} \right)_{V, ~ n} = \frac{1}{T} \left( \frac{\partial U}{\partial T} \right)_{V, ~ n} \]

式(5)に適用すれば次式が得られます。

\[ \frac{1}{T_1} \left(\frac{\partial U_1(T_1; ~ V_1, ~ n_1)}{\partial T}\right)_{V, ~ n} \delta T_1 + \frac{1}{T_2} \left(\frac{\partial U_2(T_2; ~ V_2, ~ n_2)}{\partial T}\right)_{V, ~ n} \delta T_2 = 0 \]

更に、いま各部屋の体積が一定であることに留意して、内部エネルギーの全微分を考えると

\[ \begin{align*} \text{eq(8.1)} ~~~~~ & \delta U = \left( \frac{\partial U}{\partial T} \right)_{V, ~ n} \delta T + \left( \frac{\partial U}{\partial V} \right)_{T, ~ n} \delta V \\[20pt] \text{eq(8.2)} ~~~~~ & \xrightarrow{~ \delta V = 0 ~} ~ \delta U = \left( \frac{\partial U}{\partial T} \right)_{V, ~ n} \delta T \end{align*} \]

となるので、式(7)は次のように書き換えることができます。

\[ \frac{1}{T_1} \delta U_1(T_1; ~ V_1, ~ n_1) + \frac{1}{T_2} \delta U_2(T_2; ~ V_2, ~ n_2) = 0 \]

断熱系は外界へ仕事しない限り内部エネルギーに変化は生じないため、すなわちそれぞれの部屋の内部エネルギー変化の総和は次式で示す通り 0 となります。

\[ \delta U_1(T_1; ~ V_1, ~ n_1) + \delta U_2(T_2; ~ V_2, ~ n_2) = 0 \]

式(9)および式(10)から \(\delta U_2\) を消去すると

\[ \left(\frac{1}{T_1} - \frac{1}{T_2}\right) \delta U_1(T_1; ~ V_1, ~ n_1) = 0 \]

が得られます。

式(11)は揺らぎ \(\delta U_1\) の大きさに依らず恒等的に成立する必要があるため、その条件は

\[ T_1 = T_2 \]

であると言えます。

こうして系が平衡状態にあるとき、2つの部屋は等しい温度になることが分かりました。部屋を任意の物体に置き換えれば、接触した2物体が平衡状態では等しい温度を取ることを理解できるでしょう。

圧力のつり合い

前節で扱った断熱容器の仕切りが動かせる場合について考えてみましょう。

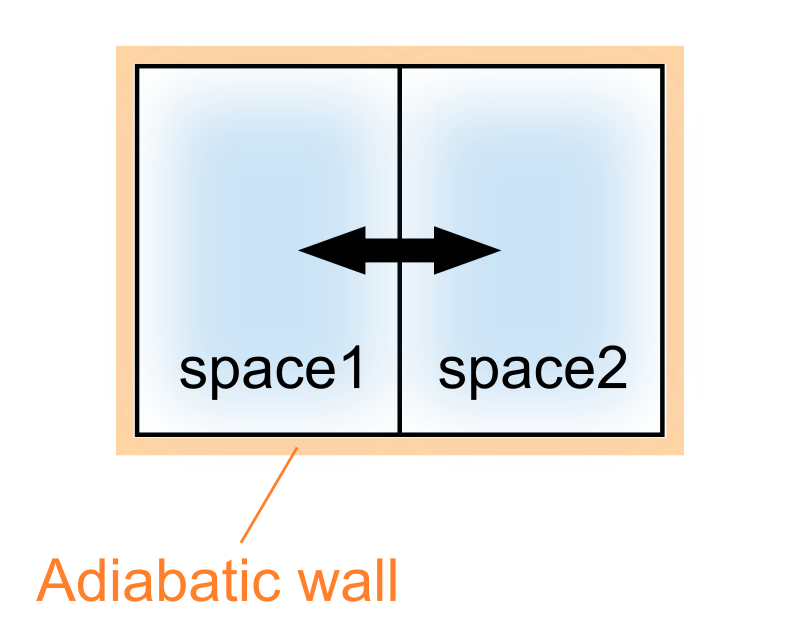
このとき、各部屋の体積が可変となるので、同時に各部屋の圧力も変化します。

平衡状態では、仕切りは適当な位置で静止することになりますが、その条件とは一体どのように記述されるでしょうか。

私達は物体の運動がつり合うとき、それは物体に加わる力の合力がちょうど 0 になる事を知っています。

同じ様に仕切りのつり合いについても、経験的に両方から加わる圧力が等しくなる位置で静止することを理解していることでしょう。

エントロピーの法則から各部屋の温度が等しい事を確認できたように、圧力が等しくなる事も確認できます。

前節ではある状態からの微小な温度の揺らぎに着目して、平衡条件の下で解析を行いました。

圧力について知見を得るには、体積の揺らぎについて考えるのが良いでしょう。

初めに状況を確認しておくと、仕切られた容器の各部屋には \(n_1\) および \(n_2\) の物質が封入されており、\(V_1\), \(V_2\) の体積を持つとします。また平衡状態では各部屋の温度は等しく \(T_1 = T_2\) とします。

平衡条件が成立する範囲で体積の揺らぎを考えると

\[ \begin{align*} \text{eq(13.1)} ~~~~~ &S\big( (T_1; ~ V_1, ~ n_1), ~ (T_2; ~ V_2, ~ n_2) \big) = S\big( (T_1; ~ V_1 + \delta V_1, ~ n_1), ~ (T_2; ~ V_2 + \delta V_2, ~ n_2) \big) \\[15pt] \text{eq(13.2)} ~~~~~ &\Rightarrow ~ S_1(T_1; ~ V_1, ~ n_1) + S_2(T_2; ~ V_2, ~ n_2) = S_1(T_1; ~ V_1 + \delta V_1, ~ n_1) + S_2(T_2; ~ V_2 + \delta V_2, ~ n_2) \end{align*} \]

と書くことができます。

式(13.2)の右辺をテイラー1次近似によって展開すると

\[ \begin{align*} S_1(T_1; ~ V_1 + \delta V_1, ~ n_1) = S_1(T_1; ~ V_1, ~ n_1) + \left(\frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial V}\right)_{T, ~ n} \delta V_1 \\[15pt] S_2(T_2; ~ V_2 + \delta V_2, ~ n_2) = S_2(T_2; ~ V_2, ~ n_2) + \left(\frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial V}\right)_{T, ~ n} \delta V_2 \end{align*} \]

となるので、結局 式(13)は次のように整理されます。

\[ \left(\frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial V}\right)_{T, ~ n} \delta V_1 + \left(\frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial V}\right)_{T, ~ n} \delta V_2 = 0 \]

エントロピーの体積に関する偏微分係数は、温度と物質量を固定する条件の下で次の関係式が成立します。( ※詳しくはエントロピーの解説ページへ。)

\[ \left(\frac{\partial S}{\partial V}\right)_{T, ~ n} = \frac{1}{T} \left\{ \left(\frac{\partial U}{\partial V}\right)_{T, ~ n} + P \right\} \]

式(16)を用いると式(15)は次のように書き換わります。

\[ \frac{1}{T_1} \left\{ \left(\frac{\partial U_1(T_1; ~ V_1, ~ n_1)}{\partial V}\right)_{T, ~ n} + P_1(T_1; ~ V_1, ~ n_1) \right\} \delta V_1 + \frac{1}{T_2} \left\{ \left(\frac{\partial U_2(T_2; ~ V_2, ~ n_2)}{\partial V}\right)_{T, ~ n} + P_2(T_2; ~ V_2, ~ n_2) \right\} \delta V_2 = 0 \]

両辺温度 \(T_1 ( ~ = T_2 ~ )\) を掛けて整理すると

\[ \left( \frac{\partial U_1(T_1; ~ V_1, ~ n_1)}{\partial V} \right)_{T, ~ n} \delta V_1 + P_1(T_1; ~ V_1, ~ n_1) \delta V_1 + \left( \frac{\partial U_2(T_2; ~ V_2, ~ n_2)}{\partial V} \right)_{T, ~ n} \delta V_2 + P_2(T_2; ~ V_2, ~ n_2) \delta V_2 = 0 \]

ここで、温度変化がない条件で内部エネルギーの全微分を考えて

\[ \begin{align*} \text{eq(19.1)} ~~~~~ &\delta U = \left( \frac{\partial U}{\partial T} \right)_{V, ~ n} \delta T + \left( \frac{\partial U}{\partial V} \right)_{T, ~ n} \delta V \\[20pt] \text{eq(19.2)} ~~~~~ &\xrightarrow{ ~ \delta T = 0 ~ } ~ \delta U = \left( \frac{\partial U}{\partial V} \right)_{T, ~ n} \delta V \end{align*} \]

式(19.2)を用いれば式(18)は次のようになります。

\[ \delta U_1(T_1; ~ V_1, ~ n_1) + P_1(T_1; ~ V_1, ~ n_1) \delta V_1 + \delta U_2(T_2; ~ V_2, ~ n_2) + P_2(T_2; ~ V_2, ~ n_2) \delta V_2 = 0 \]

断熱系では、式(10)で示したように外界に仕事をしない限り内部エネルギーの変化はなく、\(\delta U_1 + \delta U_2 = 0\) を満たします。

また、容器の総体積は一定であるため、各部屋の体積揺らぎの総和は 0 です。

\[ \delta V_1 + \delta V_2 = 0 \]

これらの事に留意すれば、式(20)は更に次のようになります。

\[ \big( P_1(T_1; ~ V_1, ~ n_1) - P_2(T_2; ~ V_2, ~ n_2) \big) \delta V_1 = 0 \]

式(22)は揺らぎ \(\delta V_1\) の大きさに依らず恒等的に成立する必要があり、そこから各部屋の圧力が等しいという条件が導かれます。

\[ P_1(T_1; ~ V_1, ~ n_1) = P_2(T_2; ~ V_2, ~ n_2) \]

物質移動を支配する熱力学量

前節までに紹介してきた、2つの部屋の温度や圧力のつり合いは、エントロピー \(S(T; ~ V, ~ n)\) がもつ変数である温度 \(T\) と体積 \(V\) の平衝点付近での揺らぎに着目して導出することができました。

エントロピーはもう1つ 物質量 \(n\) を変数にもち、物質量の揺らぎから導かれる平衡概念を考えることはできるでしょうか。

例えば半透膜を利用した次のような容器を考えてみましょう。

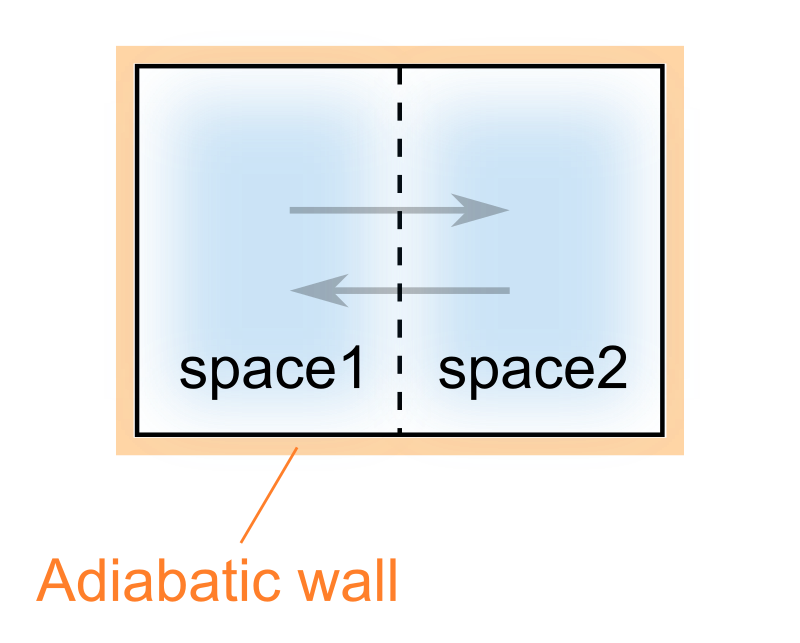
半透膜とは特定の物質のみをすり抜ける事が許された特殊な膜で、容器に封入された物質は半透膜をくぐって各部屋を行き来できるものとします。

※それはつまり半透膜はあってないようなもの？…と思われるかも知れませんが、2成分以上の系を扱うようになると部材としての機能性はもちろん、理論的概念としても非常に重要な役割を果たしてくれます。

半透膜の位置は固定し、各部屋の体積は \(V_1\), \(V_2\) から変化しない様にします。また平衡状態では各部屋の温度が等しく \(T_1 = T_2\) になるとしましょう。

平衡状態における各部屋の物質量は \(n_1\), \(n_2\) であるとき、各部屋の物質量の揺らぎに着目した平衡条件を示すと

\[ \begin{align*} \text{eq(24.1)} ~~~~~ &S\big( (T_1; ~ V_1, ~ n_1), ~ (T_2; ~ V_2, ~ n_2) \big) = S\big( (T_1; ~ V_1, ~ n_1 + \delta n_1), ~ (T_2; ~ V_2, ~ n_2 + \delta n_2) \big) \\[15pt] \text{eq(24.2)} ~~~~~ &\Rightarrow ~ S_1(T_1; ~ V_1, ~ n_1) + S_2(T_2; ~ V_2, ~ n_2) = S_1(T_1; ~ V_1, ~ n_1 + \delta n_{1}) + S_2(T_2; ~ V_2, ~ n_2 + \delta n_2) \end{align*} \]

式(24.2)の右辺をテイラー1次近似によって展開すると

\[ \begin{align*} S_1(T_1; ~ V_1, ~ n_1 + \delta n_1) = S_1(T_1; ~ V_1, ~ n_1) + \left(\frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial V}\right)_{T, ~ n} \delta n_1\\[15pt] S_2(T_2; ~ V_2, ~ n_2 + \delta n_2) = S_2(T_2; ~ V_2, ~ n_2) + \left(\frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial V}\right)_{T, ~ n} \delta n_2 \end{align*} \]

となるので、結局 式(24)は次のように整理されます。

\[ \left(\frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial n}\right)_{T, ~ V} \delta n_1 + \left(\frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial n}\right)_{T, ~ V} \delta n_2 = 0 \]

ここで容器に封入された物質は各部屋間を物質が行き来したとしても、その総物質量が変化することはありません。

要するに、各部屋における物質量揺らぎの総和は 0 となり、

\[ \delta n_1 + \delta n_2 = 0 \]

が成立する必要があります。

この事から、式(26)は次のように書き換えることができます。

\[ \left\{ \left(\frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial n}\right)_{T, ~ V} - \left(\frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial n}\right)_{T, ~ V} \right\} \delta n_1 = 0 \]

式(28)は揺らぎ \(\delta n_1\) の大きさに依らず恒等的に成立する必要があるので、次の関係が成立します。

\[ \left(\frac{\partial S_1(T_1; ~ V_1, ~ n_1)}{\partial n}\right)_{T, ~ V} = \left(\frac{\partial S_2(T_2; ~ V_2, ~ n_2)}{\partial n}\right)_{T, ~ V} \]

式(29)で与えられるように、物質の移動に関する平衡条件は各部屋におけるエントロピーの物質量に関する偏微分係数が等しくなる事が分かります。

エントロピーの物質量に関する偏微分係数は「化学ポテンシャル」と呼ばれる熱力学量を用いて表現することができます。

化学ポテンシャルとは物質移動を記述する物理量であり、当サイト内でも様々な熱力学現象を説明してくれる非常に強力な概念です。

詳細は下記のページへ譲りますが、結果のみを示すと、化学ポテンシャルを \(\mu\) としたとき次の関係式が成立します。

\[ \frac{\mu}{T} = - \left( \frac{\partial S}{\partial n} \right)_{\textcolor{red}{U}, ~ V} \]

ただし注意しなければならないのはエントロピーを偏微分するときにどの変数を固定するかで、式(30)を注意して見ると内部エネルギー \(U\) と体積 \(V\) が固定されていることが分かるでしょう。

要するにエントロピーは \(S(U, ~ V, ~ n)\) という表示で扱う必要があり、上記で見てきたような \(S(T; ~ V, ~ n)\) とは少し異なるという事です。

とは言え、別の変数を利用しているだけであり、どちらも同じエントロピーです ( 当然変数が異なるからといって、取る値が異なるなどもありません ) 。

この2つを繋ぐには温度 \(T\) から内部エネルギー \(U\) への変数変換をすれば良く、ちょうど内部エネルギー \(U(T; ~ V, ~ n)\) が温度 \(T\) に対して単調に増加する性質を持つことから得られる逆関数 \(T(U, ~ V, ~ n)\) を利用できます。

\[ \begin{align*} &S(U, ~ V, ~ n) \equiv S\big( T(U, ~ V, ~ n); ~ V, ~ n \big) \\[15pt] \Leftrightarrow ~ &S(T; ~ V, ~ n) \equiv S\big( U(T; ~ V, ~ n), ~ V, ~ n \big) \end{align*} \]

そして \(T = T(U, ~ V, ~ n)\) として式(29)を書き換えたのが次式になります。

\[ \begin{gather*} \left(\frac{\partial S_1\big( T_1(U_1, ~ V_1, ~ n_1); ~ V_1, ~ n_1 \big)}{\partial n}\right)_{U, ~ V} = \left(\frac{\partial S_2\big( T_2(U_2, ~ V_2, ~ n_2); ~ V_2, ~ n_2 \big)}{\partial n}\right)_{U, ~ V} \\[30pt] \therefore ~ \left(\frac{\partial S_1(U_1, ~ V_1, ~ n_1)}{\partial n}\right)_{U, ~ V} = \left(\frac{\partial S_2(U_2, ~ V_2, ~ n_2)}{\partial n}\right)_{U, ~ V} \end{gather*} \]